Hình bình hành là gì? Hình bình hành là một trọng những hình học quen thuộc đối với các em học sinh từ cấp tiểu học đến trung học phổ thông. Dưới đây là định nghĩa, tính chất, công thức liên quan và ứng dụng của loại hình học này, cùng theo dõi ngay!
Hình bình hành là gì?
Hình bình hành là một tứ giác đặc biệt có 2 cặp cạnh đối song song và bằng nhau. Đây là một trong những hình học cơ bản mà học sinh cần phải học trong chương trình toán. Khi bước vào lớp 4, các em học sinh sẽ chính thức được giới thiệu về hình bình hành.
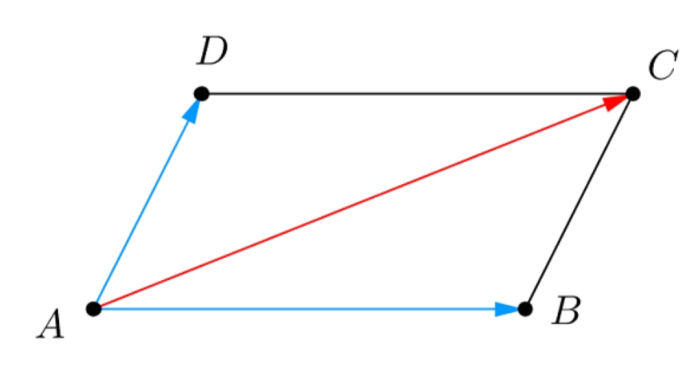
Tính chất hình bình hành
Từ định nghĩa hbh là gì, có thể thấy đây là một dạng hình thang đặc biệt (hình bình hành là hình thang có 2 cạnh bên song song). Do đó, nó sẽ có các tính chất của hình thang cân cộng với một số đặc điểm riêng nữa. Dưới đây là các tính chất của hình bình hành mà các em học sinh cần phải ghi nhớ để làm bài tập tốt hơn:
- Hình bình hành có các cạnh đối song song và bằng nhau.
- Hình bình hành có các góc đối bằng nhau.
- Hình bình hành có 2 đường chéo cắt nhau tại trung điểm mỗi đường.
Như vậy qua định nghĩa và tính chất, để chứng minh một tứ giác là hình bình hành thì chỉ cần dựa vào các dấu hiệu nhận biết hình bình hành dưới đây:
- Tứ giác có 2 cặp cạnh đối song song là hình bình hành.
- Tứ giác có 2 cặp cạnh đối bằng nhau là hình bình hành.
- Tứ giác có 2 cặp cạnh đối song song và bằng nhau là hình bình hành.
- Tứ giác có các cặp góc đối bằng nhau là hình bình hành.
- Tức giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
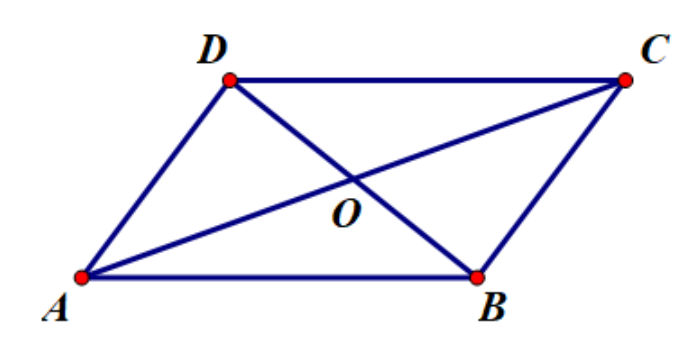
Công thức tính diện tích và chu vi hình bình hành
Về công thức liên quan đến hình bình hành, các em học sinh cần nắm vững cách tính chu vi và diện tích của hình học này. Cụ thể như sau:
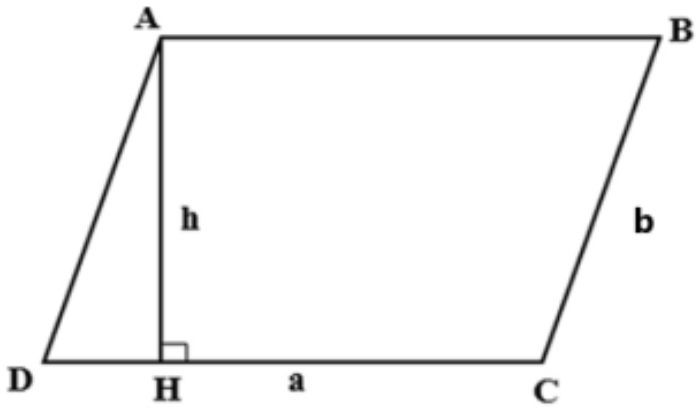
Công thức tính diện tích hình bình hành: $$S\;=\;a\;\times\;h$$
Trong đó:
- S là diện tích của hình bình hành
- a là độ dài cạnh đáy của hình bình hành
- h là đường cao của hình bình hành
Ví dụ: Cho hình bình hành ABCD có độ dài cạnh AB bằng 3cm, đường cao AH bằng 4cm. Tính diện tích hình bình hành ABCD.
Giải: Ta có diện tích hình bình hành ABCD bằng 3 x 4 =12cm2
Công thức tính chu vi hình bình hành: $$C\;=\;2\;\times\;(a\;+\;b)$$
Trong đó:
- C là chu vi của hình bình hành.
- a và b là 2 cạnh liền kề của hình bình hành.
Ví dụ: Cho hình bình hành ABCD có độ dài cạnh AB = 4cm, AC = 5cm. Tính chu vi hình bình hành ABCD.
Giải: Ta có chu vi hình bình hành ABCD bằng 2 x (4 + 5) = 18cm
5 dấu hiệu nhận biết hình bình hành
Để xác định và nhận biết một hình có phải là hình bình hành hay không, bạn sẽ dựa vào các dấu hiệu sau:
- Tứ giác có các cạnh đối song song: Cạnh đối của hình bình hành song song và không bao giờ cắt nhau.
- Tứ giác có các cạnh đối bằng nhau: Các cạnh đối trong tứ giác có độ dài giống nhau chính là hình bình hành.
- Tứ giác có hai cặp cạnh đối song song và bằng nhau: Nếu tứ giác có hai cặp cạnh đối song song và các cạnh trong cùng một cặp có độ dài bằng nhau, thì đó là một hình bình hành.
- Tứ giác có các góc đối bằng nhau: Nếu tất cả các góc trong tứ giác có giá trị bằng nhau thì tứ giác đó là hình bình hành.
- Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường chéo: Nếu hai đường chéo của tứ giác cắt nhau tại trung điểm của mỗi đường thì đó là hình bình hành.
Một số dạng bài tập về hình bình hành
Để ghi nhớ định nghĩa, tính chất hình bình hành là gì, các em học sinh hãy luyện tập nhiều các dạng bài sau:
- Dạng 1: Sử dụng tính chất của hình bình hành để chứng minh các tính chất hình học.
Ví dụ: Cho hình bình hành ABCD có E và F lần lượt là trung điểm của AB và CD. Chứng minh AF // CE.
Giải:
Vì ABCD là hình bình hành
=> AB = CD và AB // CD
Vì E và F là trung điểm của AB và CD
=> AE = EB = CF = DF
Tứ giác AECF có AE = CF và AE // CF
=> AECF là hình bình hành => AF // CE
- Dạng 2: Chứng minh hình bình hành
Ví dụ: Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G. M và N lần lượt là trung điểm của GC và GB. Chứng minh MNED là hình bình hành.
Giải:
Tam giác ABC có E là trung điểm AB, D là trung điểm AC
=> ED là đường trung bình của tam giác ABC
=> ED // BC và ED = ½ BC
Chứng minh tương tự với tam giác GBC có MN // BC và MN = ½ BC
=> MNED là hình bình hành
- Dạng 3: Chứng minh 3 điểm thẳng hàng, các đường đồng quy
Ví dụ: Cho hình bình hành ABCD, có N thuộc AB, M thuộc CD và AN = CM. Chứng minh AC, MN và BD đồng quy.
Giải:
Gọi O là giao điểm của AC và BD
=> O là trung điểm của AC
Ta có tứ giác ANCM là hình bình hành do có AN = MC và AN // MC
=> O là trung điểm của AC và MN
=> O là trung điểm của AC, MN, BD hay 3 đường cắt nhau tại O.
Ứng dụng của hình bình hành trong thực tế
Hình bình hành sở hữu nhiều tính chất đặc biệt nên có nhiều ứng dụng trong đời sống. Những ứng dụng của hình học này giúp tối ưu không gian sử dụng và tăng tính thẩm mỹ cho từng công trình, đồ đạc, thiết bị,… Dưới đây là một số ứng dụng thực tế của hình bình hành:
- Kiến trúc và xây dựng: Có nhiều cửa sổ, cửa ra vào, mái nhà được thiết kế và xây dựng theo dạng hình bình hành để tạo nên không gian mở và tăng ánh sáng tự nhiên cho căn nhà.
- Thiết kế sản phẩm: Một số đồ vật như bàn ghế, gương, thảm, khung tranh thường được làm thành hình bình hành nhằm tiết kiệm diện tích, tạo điểm nhấn và sự thoải mái khi sử dụng.
- Nghệ thuật: Hình bình hành cũng là một trong những họa tiết nổi bật được dùng khi vẽ trang, thuê, gấp giấy,…

Bài viết trên đây đã giúp các em học sinh hiểu rõ hình bình hành là gì. Hy vọng rằng qua những thông tin trên, các em học sẽ nắm rõ định nghĩa, tính chất, dấu hiệu nhận biết, công thức và ứng dụng của hình học này để làm tốt các bài tập trên lớp.




