Hình ngũ giác là gì và cách tính diện tích, tính chất cơ bản trong toán học

Hình ngũ giác là gì? Trong toán học, hình ngũ giác có nhiều tính chất thú vị và ứng dụng thực tế. Tham khảo bài viết để khám phá định nghĩa, cách nhận biết và phương pháp tính toán diện tích của nó một cách dễ dàng, từ đó phát triển kỹ năng giải bài tập hiệu quả.

Hình ngũ giác là gì?

Hình ngũ giác là một hình đa giác là gì có 5 cạnh và 5 đỉnh. Đây là một trong những hình học phẳng cơ bản, được tạo thành từ 5 đoạn thẳng nối tiếp nhau và khép kín. Định nghĩa hình ngũ giác chỉ ra rằng tổng số độ của các góc trong của hình ngũ giác lồi bằng 540 độ.

Trong thực tế, hình ngũ giác xuất hiện phổ biến trong kiến trúc và thiết kế. Ví dụ như Lầu Năm Góc (The Pentagon) – trụ sở của Bộ Quốc phòng Hoa Kỳ là một công trình kiến trúc nổi tiếng có dạng hình ngũ giác là gì đều. Ngoài ra, hình ngũ giác còn được sử dụng trong thiết kế logo, đồ họa và các mẫu trang trí.

Hình ngũ giác có thể được phân loại thành nhiều dạng khác nhau như: hình ngũ giác đều (có 5 cạnh bằng nhau và 5 góc bằng nhau), hình ngũ giác lồi (các góc đều hướng ra ngoài), hình ngũ giác lõm (có ít nhất một góc hướng vào trong). Mỗi dạng hình ngũ giác đều có những tính chất và ứng dụng riêng trong thực tiễn.

Các tính chất cơ bản của hình ngũ giác trong hình học phẳng

Tính chất hình ngũ giác là những đặc điểm quan trọng giúp phân biệt và xác định hình dạng này trong hình học phẳng. Tương tự như tứ giác lồi là gì, các tính chất của hình ngũ giác được xác định thông qua số đỉnh, cạnh, góc và đường chéo. Những tính chất này có vai trò quan trọng trong việc giải các bài toán hình học.

Số đỉnh và cạnh của hình ngũ giác

Hình ngũ giác có 5 đỉnh và 5 cạnh, đây là đặc điểm cơ bản nhất để nhận biết. Các đỉnh được đánh dấu theo thứ tự A, B, C, D, E và các cạnh tương ứng là AB, BC, CD, DE, EA.

Trong hình ngũ giác đều, 5 cạnh có độ dài bằng nhau và được ký hiệu là a. Khoảng cách từ tâm đến đỉnh của hình ngũ giác đều được gọi là bán kính ngoại tiếp R, còn khoảng cách từ tâm đến cạnh được gọi là bán kính nội tiếp r.

Tổng số độ của các góc trong và góc ngoài

Tổng số độ của các góc trong của hình ngũ giác luôn bằng 540°. Con số này được tính dựa trên công thức (n-2) × 180° với n=5 là số cạnh. Trong trường hợp hình ngũ giác đều, mỗi góc trong có số đo bằng 108°.

Với góc ngoài, tổng số đo của 5 góc ngoài luôn bằng 360°. Mỗi góc ngoài của hình ngũ giác đều có số đo 72°, bằng 360° chia cho số cạnh. Đây là tính chất quan trọng giúp giải nhiều bài toán phức tạp.

Đường chéo và các tính chất liên quan

Số đường chéo của hình ngũ giác được tính theo công thức n(n-3)/2, với n=5 ta có 5 đường chéo. Các đường chéo này chia hình ngũ giác thành các tam giác nhỏ hơn.

Trong hình ngũ giác đều, các đường chéo có độ dài bằng nhau. Chúng tạo thành một ngôi sao năm cánh khi được vẽ đầy đủ. Góc giữa hai đường chéo liên tiếp là 72°, tương ứng với góc ngoài của hình ngũ giác.

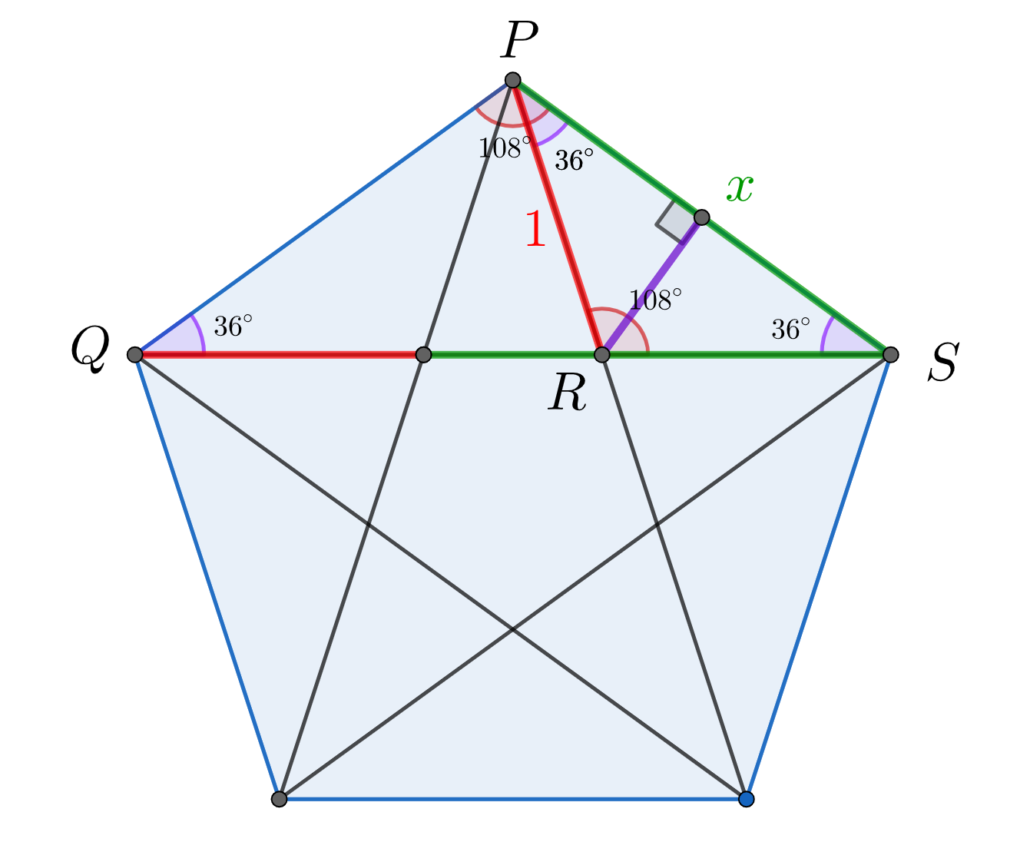
Đường chéo còn đóng vai trò quan trọng trong việc tính diện tích hình ngũ giác thông qua phương pháp chia thành các tam giác nhỏ. Điều này giúp đơn giản hóa nhiều bài toán phức tạp về diện tích.

Phân loại và đặc điểm nhận dạng các dạng hình ngũ giác

Việc phân loại và nhận dạng các dạng hình ngũ giác giúp người học dễ dàng phân biệt và áp dụng các tính chất đặc trưng. Dấu hiệu nhận biết hình ngũ giác chính là đa giác có 5 cạnh và 5 đỉnh. Mỗi loại hình ngũ giác có những đặc điểm riêng biệt cần được phân tích kỹ lưỡng.

Hình ngũ giác lồi và lõm

Hình ngũ giác lồi là hình có tất cả các góc đều hướng ra phía ngoài, mọi đường chéo đều nằm hoàn toàn bên trong hình. Khi kéo dài bất kỳ cạnh nào, các đỉnh còn lại đều nằm về một phía của đường thẳng đó.

Ngược lại, hình ngũ giác lõm có ít nhất một góc hướng vào trong, tồn tại đường chéo nằm một phần hoặc toàn bộ bên ngoài hình. Dấu hiệu nhận biết HNG lõm là khi kéo dài một cạnh, các đỉnh còn lại không cùng nằm về một phía của đường thẳng đó.

Hình ngũ giác đều và không đều

Hình ngũ giác đều là gì – một dạng đặc biệt với 5 cạnh bằng nhau và 5 góc bằng nhau, mỗi góc có số đo 108°. Hình này có tính đối xứng cao, có thể xoay quanh tâm với góc 72° mà vẫn trùng khít với hình ban đầu.

Hình ngũ giác không đều có các cạnh hoặc các góc không bằng nhau. Loại hình này phổ biến hơn trong thực tế và có nhiều biến thể khác nhau tùy thuộc vào độ dài các cạnh và số đo các góc.

Hình ngũ giác nội tiếp và ngoại tiếp

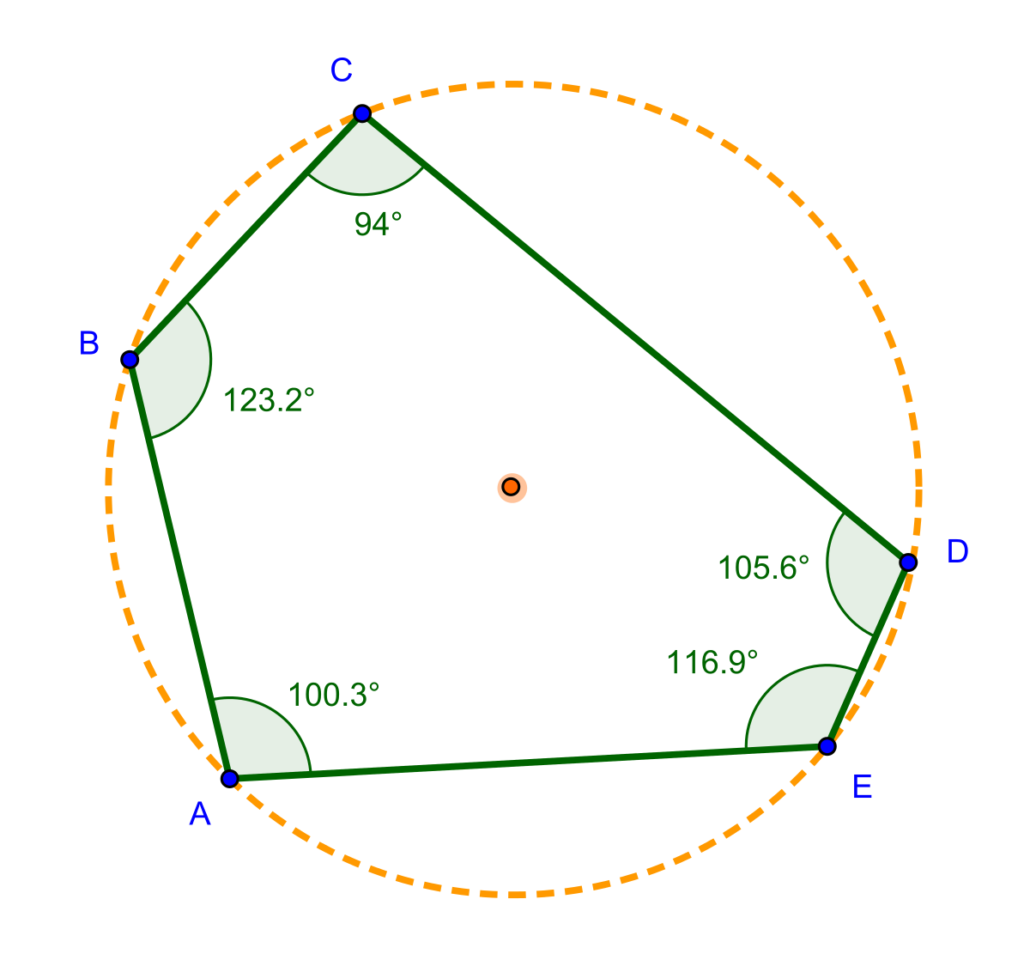
Tương tự như tính chất tứ giác nội tiếp, hình ngũ giác nội tiếp là hình có tất cả các đỉnh nằm trên một đường tròn. Đặc điểm quan trọng là tổng các góc lẻ bằng tổng các góc chẵn.

Hình ngũ giác ngoại tiếp có tất cả các cạnh tiếp xúc với một đường tròn. Trong trường hợp này, các đường vuông góc từ tâm đường tròn đến các cạnh của hình ngũ giác đều bằng nhau và bằng bán kính đường tròn ngoại tiếp.

Cách tính diện tích hình ngũ giác trong các trường hợp

Việc tính diện tích hình ngũ giác phụ thuộc vào đặc điểm của hình – đều hay không đều. Công thức diện tích hình ngũ giác sẽ khác nhau trong từng trường hợp cụ thể. Tương tự như hình thoi là gì lớp 4, việc nắm vững các công thức và phương pháp tính diện tích sẽ giúp giải quyết nhiều bài toán hình học.

Với hình ngũ giác đều, ta có thể áp dụng công thức trực tiếp. Còn với hình ngũ giác không đều, phương pháp chia nhỏ thành các hình cơ bản sẽ phù hợp hơn. Mỗi phương pháp đều có ưu điểm riêng tùy thuộc vào dạng bài toán cụ thể.

Công thức tính diện tích hình ngũ giác đều

Đối với hình ngũ giác đều, ta có thể áp dụng công thức: S = (5 × a × R)/2, trong đó a là độ dài cạnh và R là bán kính đường tròn ngoại tiếp. Công thức này được rút ra từ việc chia hình ngũ giác đều thành 5 tam giác đều bằng nhau.

Ngoài ra còn có công thức khác sử dụng apothem (đường cao từ tâm đến cạnh): S = (5 × a × h)/2, với h là độ dài apothem. Công thức này thường được ưu tiên sử dụng vì dễ xác định các yếu tố hơn.

Phương pháp chia nhỏ để tính diện tích hình ngũ giác không đều

Với hình ngũ giác không đều, phương pháp hiệu quả nhất là chia thành các hình tam giác. Bằng cách vẽ các đường chéo từ một đỉnh đến các đỉnh không liền kề, ta sẽ chia được hình ngũ giác thành 3 tam giác.

Sau khi chia nhỏ, ta tính diện tích từng tam giác bằng công thức S = (a × h)/2 hoặc công thức Heron tùy thuộc vào dữ kiện cho trước. Tổng diện tích các tam giác thành phần chính là diện tích của hình ngũ giác ban đầu.

Phương pháp này đặc biệt hữu ích khi giải các bài toán thực tế như tính diện tích mảnh đất, khu vực xây dựng có hình dạng ngũ giác không đều. Việc chia nhỏ giúp tính toán chính xác và dễ kiểm chứng kết quả.

Ứng dụng của hình ngũ giác trong thực tế và bài tập

Hình ngũ giác có nhiều ứng dụng quan trọng trong cuộc sống, từ kiến trúc đến thiết kế công nghiệp. Hình ngũ giác trong thực tế xuất hiện phổ biến ở các công trình nổi tiếng như Lầu Năm Góc (Pentagon) tại Mỹ hay các mẫu thiết kế nội thất hiện đại. Cấu trúc đặc biệt của hình ngũ giác mang lại sự cân bằng và tính thẩm mỹ cao.

Ngoài ra, hình ngũ giác còn được ứng dụng trong nhiều lĩnh vực khác như thiết kế logo, đồ họa và hình lục giác là gì. Các nhà thiết kế thường kết hợp hình ngũ giác với các hình học khác để tạo ra những tác phẩm độc đáo và ấn tượng.

Các ví dụ về hình ngũ giác trong kiến trúc và thiết kế

Một trong những ví dụ hình ngũ giác tiêu biểu là Nhà hát Opera Sydney, nơi các mảng tường được thiết kế theo dạng ngũ giác để tạo hiệu ứng thị giác đặc biệt. Theo kiến trúc sư Jørn Utzon, việc sử dụng hình ngũ giác giúp công trình có được sự cân bằng hoàn hảo giữa các yếu tố.

Trong lĩnh vực thiết kế nội thất, các nhà thiết kế thường sử dụng hình ngũ giác cho gạch lát sàn hoặc trang trí tường. Theo nghiên cứu của Viện Thiết kế Nội thất Hoa Kỳ, mẫu hình ngũ giác có khả năng tạo chiều sâu và không gian ảo giác, giúp phòng trông rộng rãi hơn.

Các công trình tôn giáo cũng thường xuyên sử dụng hình ngũ giác trong thiết kế cửa sổ và mái vòm. Điều này không chỉ mang ý nghĩa tâm linh mà còn tạo ra những hiệu ứng ánh sáng độc đáo.

Bài tập và phương pháp giải về hình ngũ giác

Bài tập hình ngũ giác thường tập trung vào việc tính diện tích, chu vi và các yếu tố liên quan. Để giải các bài toán này hiệu quả, cần nắm vững công thức và phương pháp tiếp cận phù hợp.

Một phương pháp giải phổ biến là chia hình ngũ giác thành các tam giác nhỏ hơn. Kỹ thuật này giúp đơn giản hóa việc tính toán và áp dụng các công thức cơ bản của tam giác. Theo thống kê của các giáo viên toán học, học sinh thường đạt kết quả tốt hơn khi áp dụng phương pháp này.

Việc vẽ hình ngũ giác cũng là một kỹ năng quan trọng cần rèn luyện. Sử dụng compa và thước kẻ, học sinh có thể thực hành vẽ hình ngũ giác đều hoặc bất kỳ. Điều này giúp phát triển tư duy không gian và kỹ năng hình học thực hành.

Hình ngũ giác là gì? Đây là một khái niệm quan trọng trong hình học với nhiều đặc điểm và tính chất thú vị. Qua việc tìm hiểu các tính chất hình ngũ giác, cách tính diện tích và ứng dụng thực tế, bạn sẽ có cái nhìn sâu sắc hơn về hình học. Việc nắm vững định nghĩa cùng các yếu tố liên quan sẽ giúp ích rất nhiều trong việc giải toán và áp dụng vào thực tiễn.