Diện tích hình tam giác là kiến thức quan trọng trong chương trình học hiện nay. Nắm rõ công thức này là điều cần thiết đối với học sinh các cấp. Cùng tìm hiểu về các công thức tính diện tích cho các loại hình tam giác từ cơ bản đến nâng cao.
Công thức tính diện tích hình tam giác
Ngoài tam giác thường sẽ có một số hình tam giác đặc biệt như tam giác cân, tam giác đều, tam giác vuông,… Các cách tính diện tích hình tam giác của từng loại như sau:
Cách tính diện tích tam giác thường
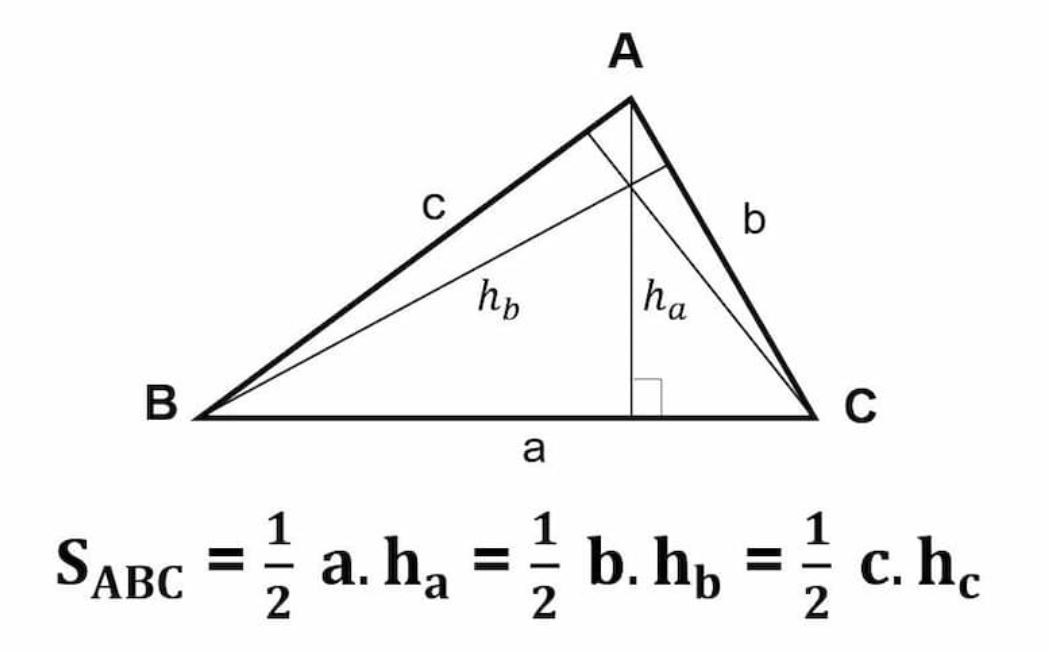
Tam giác thường là hình có 3 cạnh, tổng 3 góc trong bằng 180 độ và không có tính chất đặc biệt nào khác. Công thức để tìm diện tích hình tam giác thường sẽ như sau:
$$S=\frac12\times a\times h$$
Trong đó S là dt hình tam giác; a là chiều dài của cạnh đáy; h là chiều cao từ đỉnh xuống cạnh đáy.
Xem thêm: Cách tính chu vi hình tam giác
Công thức tính diện tích tam giác vuông
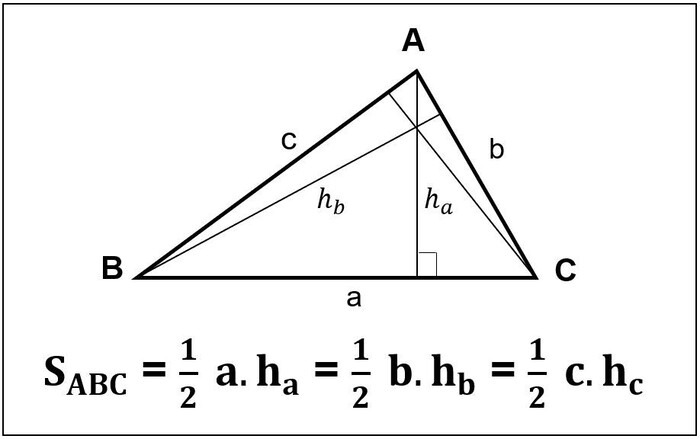
Tam giác vuông là loại tam giác có 1 góc trong bằng 90 độ. 2 cạnh của hình tạo thành góc 90 độ được gọi là cạnh góc vuông, còn lại sẽ là cạnh huyền. Công thức để tính diện tích hình tam giác vuông như sau:
$$S\;=\frac12\times a\times b$$
Trong đó a, b là số đo hai cạnh góc vuông của hình tam giác.
Xem thêm: Cách chứng minh hình tam giác vuông
Công thức tính diện tích tam giác cân
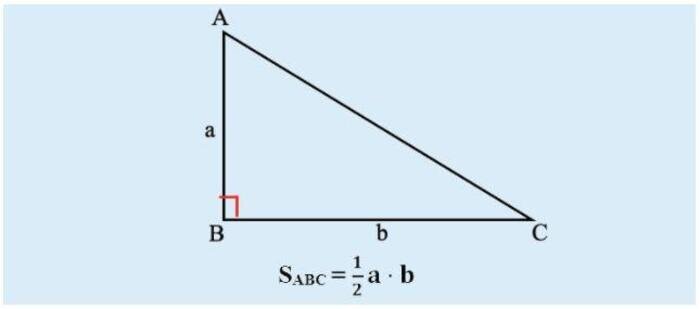
Tam giác cân là hình có hai cạnh bên bằng nhau và hai góc đáy bằng nhau. Công thức tính diện tích tam giác cân cũng như tam giác thường, đó là:
$$S\;=\frac12\times b\times h$$
Trong đó b là chiều dài cạnh đáy; h là chiều cao từ đỉnh xuống cạnh đáy.
Xem thêm: Hình tam giác cân là gì? Tính chất của tam giác cân
Tính diện tích tam giác đều
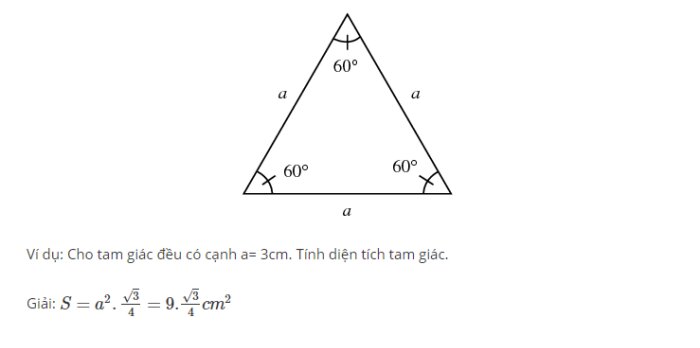
Tam giác đều là hình có 3 cạnh bằng nhau và 3 góc trong bằng nhau là 60 độ. Công thức tính ra diện tích của tgđ là:
$$S\;=a^2\times \frac{\sqrt3}4$$
Trong đó a là chiều dài 1 cạnh của hình tam giác đều.
Xem thêm: Cách chứng minh tam giác đều
Tính diện tích tam giác vuông cân
Tam giác vuông cân là tam giác có 1 góc vuông có hai cạnh tạo thành góc đó bằng nhau. Do đó công thức để tính diện tích tam giác vuông cân như sau:
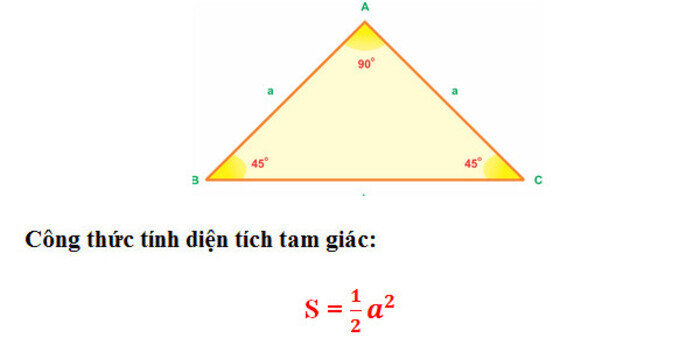
$$S\;=\frac12\times a^2$$
Trong đó a là chiều dài của 1 cạnh góc vuông.
Một số bài tập ứng dụng
Dưới đây là một số bài tập tính diện tích hình tam giác lớp 5 cơ bản nhất:
Bài tập 1: Hình tam giác có độ dài đáy là 10cm, chiều cao là 7cm. Yêu cầu tính diện tích của htg đã cho.
Lời giải: Áp dụng công thức tính diện tích hình tam giác thường, ta có dt của tg đề bài cho như sau:
S = 10 x 7 : 2 = 35 cm2
Bài tập 2: Cho một hình tam giác vuông có hai cạnh góc vuông lần lượt là 5dm và 6dm. Hãy tính diện tích của htg đó.
Lời giải: Diện tích tg vuông đề bài đã cho áp dụng công thức tính như sau:
S = 5 x 6 / 2 = 15 dm2
Bài tập 3: Hãy tính dt của hình tam giác đều ABC có độ dài của 1 cạnh là 8cm.
Lời giải: Diện tích tam giác ABC bằng:
S = √3/4 x 8^2 = 27,713 cm2
Bài tập 4: Một tam giác vuông cân có chiều dài của hai cạnh góc vuông bằng nhau là 5cm. Hỏi diện tích của hình là bao nhiêu?
Lời giải: Áp dụng công thức tính dt hình tam giác vuông cân sẽ có đáp án như sau:
S = ½ x 5^2 = 12,5 cm2
Lưu ý cần biết để giải nhanh các bài toán tính diện tích hình tam giác
Để tính diện tích htg nhanh chóng, đúng công thức nhất, bạn có thể lưu ý đến một số mẹo sau đây:
- Ghi nhớ những tính chất của từng hình tam giác: Dựa vào tính chất của hình tam giác, bạn có thể dễ dàng nhận diện được đó là hình tam giác loại nào để áp dụng công thức tính một cách nhanh chóng và dễ dàng nhất.
- Sử dụng định lý Pythagoras để tính dt hình tam giác: Công thức tính dt của một hình tam giác vuông được ứng dụng bởi định lý Pytago. Do đó khi làm bài về tam giác vuông hoàn toàn có thể sử dụng định lý này để tìm ra câu trả lời nhanh nhất cho bài giải.
- Thường xuyên làm bài luyện đề: Một cách ghi nhớ nhuần nhuyễn các công thức tính diện tích tam giác tốt nhất đó là luyện tập làm bài hàng ngày. Thông qua luyện đề, bạn sẽ có được những kiến thức rộng nhất về nhận biết loại hình tam giác, nên áp dụng công thức nào là tốt nhất, tư duy khi làm bài cũng được trau dồi hơn.
Bài viết trên đây là những thông tin về diện tích hình tam giác cơ bản và dễ hiểu nhất. Thông qua đó, giúp người đọc nắm bắt được kiến thức và vận dụng dễ dàng vào các bài tập thực tế. Nếu có bất kỳ ý kiến góp ý, bạn hãy bình luận ngay bên dưới!