Đường cao hình tam giác là một khái niệm quan trọng trong hình học, thường được dùng để tính toán diện tích. Việc hiểu về đường cao giúp chúng ta giải quyết nhiều bài toán hình học phức tạp và áp dụng vào các lĩnh vực khác nhau như kiến trúc, khoa học, công nghệ.
Định nghĩa về đường cao hình tam giác
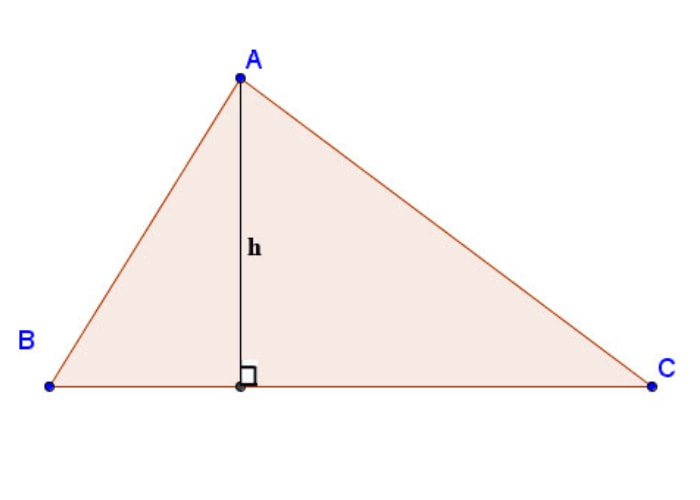
Đường cao hình tam giác là một đoạn thẳng kẻ từ một đỉnh của tam giác với cạnh đối diện và tạo thành một góc vuông tại giao điểm đó. Cạnh đối diện còn được gọi là cạnh đáy. Mỗi tam giác đều có ba đường cao và giao điểm giữa đường cao với cạnh đáy còn được gọi là chân đường cao.
Xem thêm: Tgc là gì? Cách tính, đặc điểm và ứng dụng
Phân loại đường cao trong tam giác và ví dụ chi tiết
Hiểu rõ về đường cao trong loại htg khác nhau giúp xác định các đặc tính hình học, đưa ra công thức và phương pháp đúng cho từng dạng:
- Trong tam giác cân, đường cao cũng là đường trung tuyến và phân giác từ đỉnh cân.
- Trong tam giác đều, mọi đường cao đều bằng nhau và là đường trung tuyến.
- Trong tam giác vuông, đường cao chính lạ cạnh kề góc vuông.
Ví dụ chi tiết từng dạng:
- Trong tam giác thường ABC: Đường cao từ đỉnh A xuống cạnh BC được ký hiệu là Ha. Đây là đoạn thẳng từ A đến điểm H trên BC sao cho AH vuông góc với BC.
- Trong tam giác vuông ABC: Đường cao từ đỉnh góc vuông tới cạnh huyền là một đoạn thẳng trên một trong hai cạnh góc vuông.
- Trong tam giác cân ABC: Đường cao từ đỉnh cân xuống cạnh đáy cũng là đường trung tuyến và đường phân giác.
- Trong tam giác đều: Mỗi đường cao cũng là đường trung tuyến, chia tam giác thành hai tam giác vuông bằng nhau.
Đọc thêm: Tính chất của trọng tâm và cách xác định trọng tâm tam giác trong Hình học
Tính chất của đường cao hình tam giác
Đường cao tam giác có những tính chất cụ thể sau:
- Trong mỗi tam giác, ba đường cao gặp nhau tại một điểm duy nhất, gọi là trực tâm. Đây là nơi tụ điểm của sự cân bằng của tam giác.
- Trong tam giác cân, đường cao từ đỉnh cân xuống cạnh đáy cũng là đường trung tuyến và đường phân giác, thể hiện sự đối xứng đặc biệt của tam giác cân.
- Đối với tam giác đều, ba đường cao không chỉ giao nhau tại trực tâm mà còn là các đường trung tuyến, mỗi đường cao là trục đối xứng của tam giác đều.
Những tính chất này không chỉ giúp chúng ta hiểu sâu hơn về cấu trúc của tam giác mà còn có thể áp dụng vào việc giải các bài toán hình học, từ những vấn đề đơn giản như tính diện tích đến những bài toán phức tạp hơn về các định lý và chứng minh.
Đọc ngay: Cách tính diện tích hình tam giác đơn giản, dễ hiểu
Trực tâm và mối liên hệ với đường cao trong tam giác
Trong hình học, trực tâm một tam giác là điểm giao nhau của ba đường cao. Đường cao là đoạn thẳng vuông góc từ một đỉnh đến cạnh đối diện. Mỗi tam giác có ba đường cao và chúng gặp nhau tại một điểm duy nhất, được gọi là trực tâm.
Vị trí của trực tâm có thể ở bên trong tam giác, trùng với đỉnh góc vuông của tam giác vuông hoặc ở bên ngoài tam giác, phụ thuộc vào dạng của htg (nhọn, tù hay vuông).
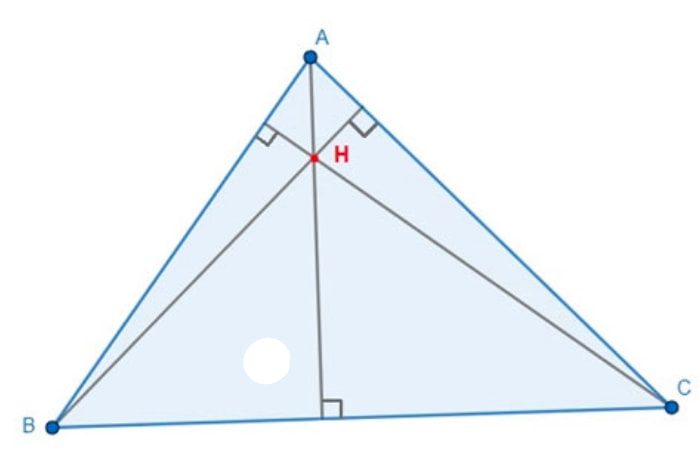
Tham khảo thêm: Tổng hợp đầy đủ các lý thuyết hai tam giác bằng nhau
Cách tính đường cao hình tam giác
Để tính đường cao của một tam giác, chúng ta có thể áp dụng các công thức và phương pháp sau đây, phụ thuộc vào loại tam giác cụ thể:
1/ Tam giác thường: Đường cao được tính bằng cách sử dụng diện tích tam giác và chiều dài cạnh tương ứng:
$$h\;=\;\frac{2\;\times\;S}d$$
Trong đó: S là diện tích tam giác, d là chiều dài cạnh đáy.
Hoặc áp dụng công thức heron để tính đường cao:
$$h\;=\;\frac{(2p(p-a)\;(p-b)\;(p-c))}a$$
Trong đó: p là nửa chu vi tam giác. Công thức tính: $$p\;=\;\frac{(a+b+c)}2$$
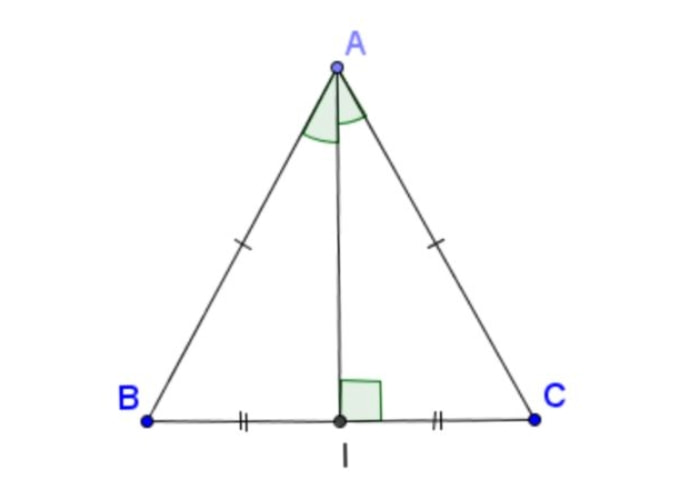
2/ Tam giác đều: Trong tam giác đều, mọi đường cao đều bằng nhau và có thể tính bằng:
$$h\;=\;\frac{a\sqrt3}2$$
Trong đó: a là độ dài cạnh tam giác đều
3/ Tam giác vuông: Trong tam vuông, đường cao từ đỉnh vuông xuống cạnh huyền có thể tính bằng cách áp dụng công thức sau:
$$h\;=\;\frac{ab}c$$
Trong đó: a,b là chiều dài của hai cạnh góc vuông, c là cạnh huyền
4/ Tam giác cân: Trong tam giác cân, đường cao từ đỉnh cân xuống cạnh đáy cũng là đường trung tuyến, có thể sử dụng công thức:
$$h\;=\;\sqrt{b^2\;-\;{(\frac a2)}^2}$$
Trong đó: là độ dài cạnh đáy, là độ dài hai cạnh bằng nhau.
Ví dụ minh họa cách tính đường cao hình tam giác
VD 1: Tính đường cao trong tam giác thường:
Cho tam giác ABC có AB = 10cm, BC = 12cm, CA = 15cm. Tính đường cao AH.
Giải:
- Bước 1: Tính diện tích tam giác ABC theo công thức Heron:
$$S\;=\sqrt{p(p\;-\;a)(P\;-\;b)(p\;-\;c)}$$
Trong đó:
- p là nửa chu vi tam giác, $$p\;=\;\frac{(AB\;+\;BC\;+\;CA)}2$$.
- a = AB, b = BC, c = CA.
Suy ra:
$$p\;=\;\frac{(10\;+\;12\;+\;15)}2\;=\;18.5$$
$$S\;=\;\sqrt{18.5(18.5\;-\;10)(18.5\;-\;12)(18.5\;-\;15)}\;\approx\;64.98\;cm^2$$
- Bước 2: Tính đường cao AH theo công thức:
$$h\;=\;\frac{2S}a=\;\frac{(2\times64.98)}{10}\approx12.99\;cm$$
Vậy đường cao AH của tam giác ABC xấp xỉ 12.99cm.
VD 2: Tính đường cao trong tam giác đều:
Cho tam giác đều ABC có cạnh a = 6cm. Tính đường cao AH.
Giải:
Áp dụng công thức tính đường cao trong tam giác đều:
$$h\;=\;\frac{a\sqrt3}2=\frac{6\;\times\;\sqrt3}2=\;\frac{6\sqrt3}2\;\approx\;5.19\;cm$$
Vậy đường cao AH của tam giác đều ABC xấp xỉ 5.19cm.
Ứng dụng của đường cao trong thực tế
Trong hình học, đường cao trong tam giác không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế quan trọng:
- Xây dựng và đo đạc: Sử dụng để đo chiều cao của các công trình như tòa nhà cao tầng hoặc cây cối.
- Trong toán học: Là công cụ quan trọng trong việc giải các bài toán hình học, tính diện tích tam giác, và chứng minh các tính chất hình học.
- Ứng dụng trong thiết kế: Được dùng để thiết kế các mô hình chính xác và các bộ phận trong máy móc, ô tô hoặc kiến trúc.
Các bài toán liên quan đến đường cao thường bao gồm:
- Chứng minh tính vuông góc của hai đường thẳng trong tam giác.
- Giải các bài toán về tam giác cân và tam giác đều, nơi đường cao cũng là đường trung tuyến, đường phân giác.
- Chứng minh rằng ba đường cao trong một tam giác gặp nhau tại một điểm duy nhất, được gọi là trực tâm của tam giác.
Việc hiểu và áp dụng các tính chất và ứng dụng của đường cao giúp chúng ta không chỉ hiểu sâu hơn về kiến thức hình học mà còn giúp giải quyết các vấn đề thực tế.

Trên đây là tổng hợp các cách tính đường cao hình tam giác, các mô tả cũng như hướng dẫn chi tiết đã được để cập. Học sinh nên ôn tập và rèn luyện làm bài tập mỗi ngày để đạt kết quả tốt hơn.