Hình trụ là gì, bao gồm những thành phần nào, đặc điểm, tính chất là gì? Đâu là những công thức toán học liên quan tới hình trụ? Cùng tìm hiểu ngay trong bài viết dưới đây.
Hình trụ là gì? Khái niệm và các thành phần của hình trụ
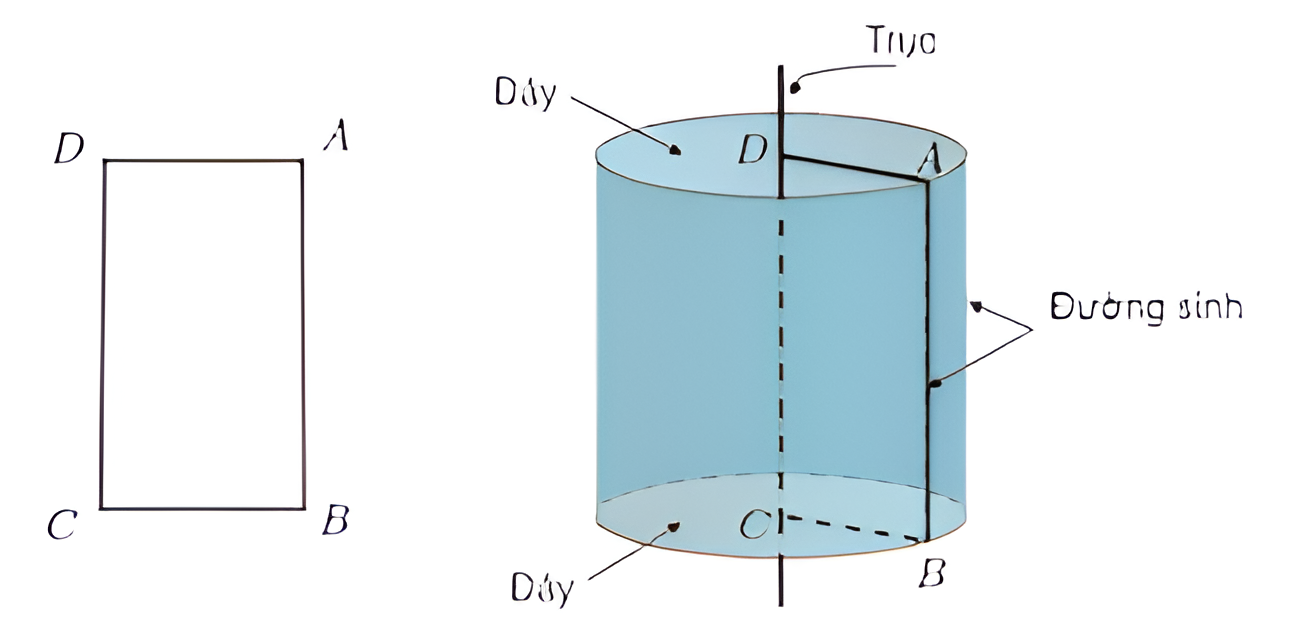
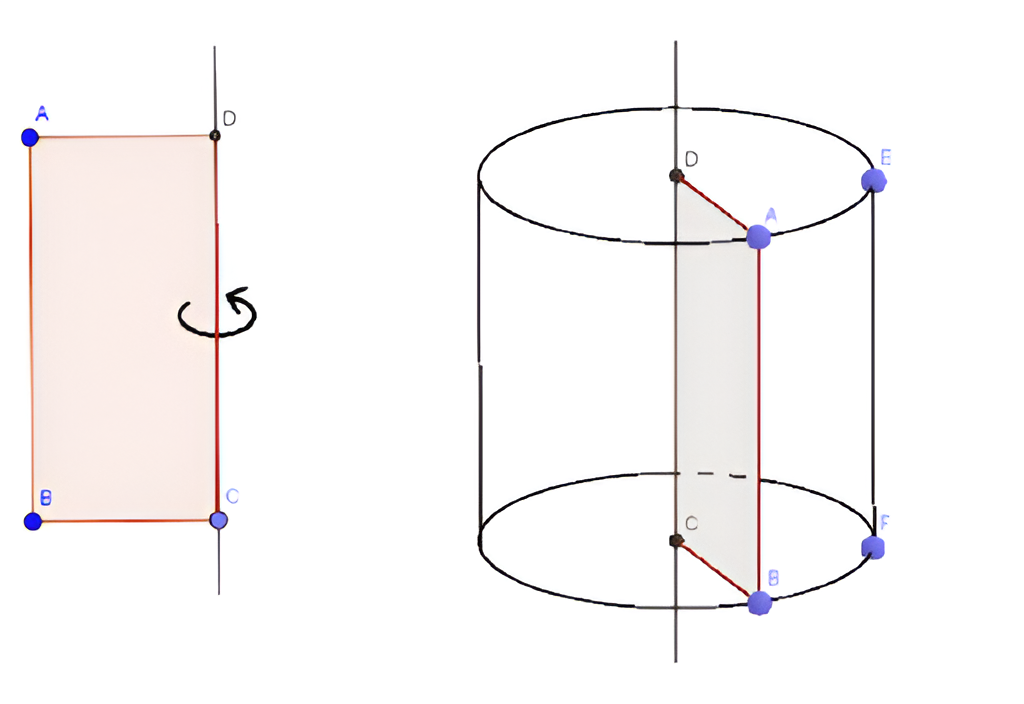
Hình trụ là một hình không gian được tạo ra bởi việc quay một hình chữ nhật quanh một trục cố định. Hình trụ bao gồm một số thành phần chính như:
- Hai mặt đáy: Là hai hình tròn bằng nhau và song song với nhau.
- Mặt xung quanh: Là một mặt phẳng hình chữ nhật được tạo ra bởi việc quay các cạnh của hình chữ nhật ban đầu.
- Trục: Là đường thẳng đi qua tâm của hai mặt đáy và vuông góc với mặt phẳng của hai mặt đáy.
- Đường sinh: Là những đường thẳng nằm trên mặt xung quanh của hình trụ và song song với trục.
Đặc điểm và tính chất của hình trụ
Một số tính chất của hình trụ bao gồm:
- Hai mặt đáy của hình trụ luôn bằng nhau và song song với nhau.
- Mặt xung quanh của hình trụ luôn là một mặt phẳng hình chữ nhật.
- Đường sinh của hình trụ luôn vuông góc với trục.
- Hình trụ có thể được chia thành hai hình chóp đều có cùng chiều cao và cùng bán kính mặt đáy.
Ngoài ra, các bạn cũng nên lưu ý một số điểm đặc biệt trên các thành phần có trong hình trụ như:
Mặt đáy:
- Tâm của hai mặt đáy trùng với nhau và nằm trên trục của hình trụ.
- Bán kính của mặt đáy bằng một nửa chiều cao của hình trụ.
Mặt xung quanh:
- Chiều cao của mặt chữ nhật bằng chiều cao của hình trụ.
- Chu vi của mặt chữ nhật bằng chu vi của một mặt đáy.
Trục: Chiều dài của trục bằng chiều cao của hình trụ.
Đường sinh: Chiều dài của đường sinh bằng chu vi của một mặt đáy
Các công thức liên quan tới hình trụ
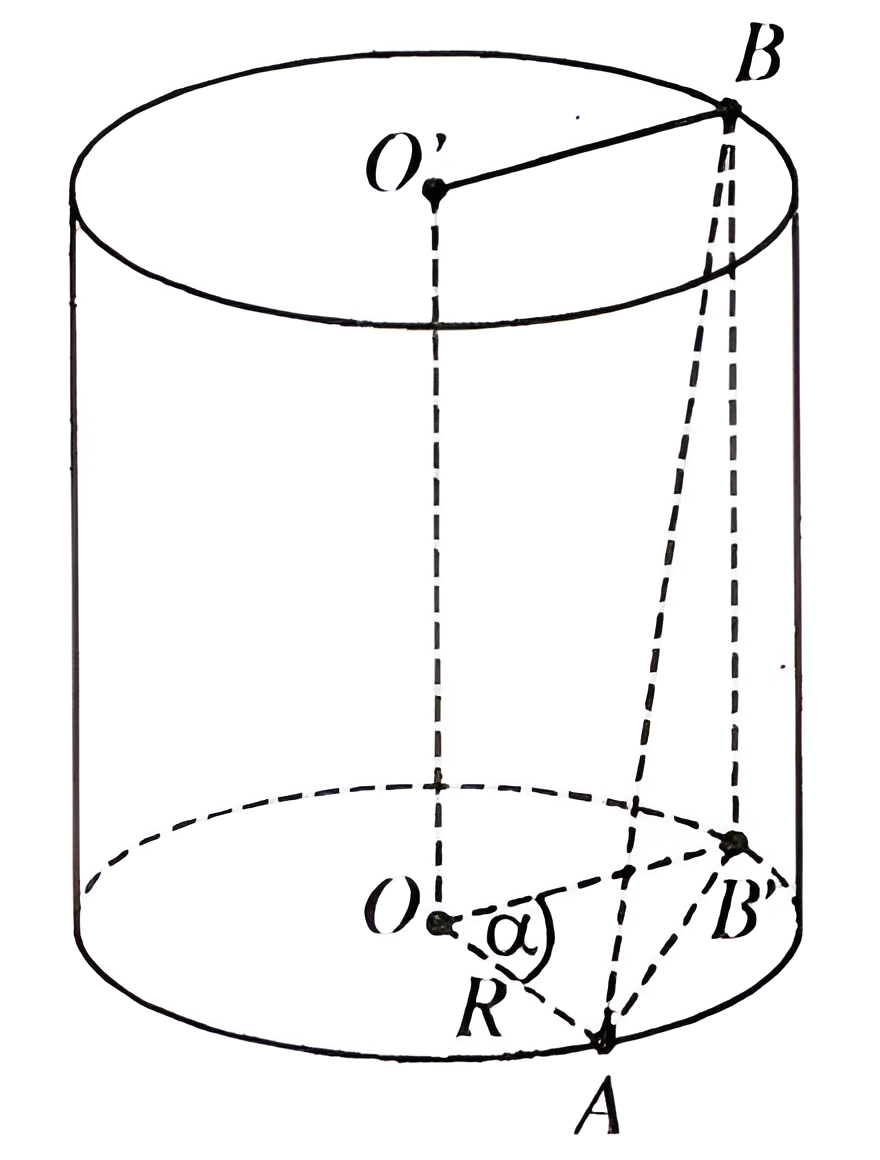
Trước khi tìm hiểu về các công thức liên quan tới hình trụ, ta cùng đi qua một số kí hiệu cơ bản trong các công thức, bao gồm:
- Bán kính mặt đáy (r): Là khoảng cách từ tâm của một mặt đáy đến bất kỳ điểm nào trên đường tròn của mặt đáy đó.
- Chiều cao (h): Là khoảng cách giữa hai mặt đáy của hình trụ.
- Độ dài đường sinh (l): Là khoảng cách từ một điểm trên đường tròn của mặt đáy này đến điểm tương ứng trên đường tròn của mặt đáy kia, theo đường thẳng song song với trục của hình trụ (áp dụng cho hình trụ nghiêng, riêng hình trụ đứng thì độ dài đường sinh bằng chiều cao ).
Chu vi hình trụ là gì? Chu vi đường tròn đáy hình trụ
Chu vi đường tròn đáy của hình trụ được tính toán bằng công thức:
$$C = 2\pi r$$
Diện tích hình trụ là gì?
Diện tích hình trụ bao gồm diện tích xung quanh, diện tích mặt đáy và diện tích toàn phần.
Diện tích xung quanh hình trụ
Diện tích xung quanh hình trụ (S_xq) là diện tích của mặt phẳng hình chữ nhật bao quanh hình trụ. Mặt phẳng này được tạo ra bởi việc quay các cạnh của hình chữ nhật ban đầu khi ta quay hình chữ nhật đó quanh một trục cố định.
Diện tích xung quanh của hình trụ được tính theo công thức:
$$S_{xq}=2\pi\times r\times h$$
Trong đó:
- S_xq là diện tích mặt xung quanh hình trụ (đơn vị: cm², m²,…)
- π là số Pi, xấp xỉ bằng 3.14159 (đơn vị không có)
Diện tích mặt đáy
Diện tích đáy của hình trụ là diện tích của một trong hai mặt đáy hình tròn. Hiểu một cách đơn giản, ta sử dụng công thức diện tích của hình tròn để tính mặt đáy.
$$S_d\;=\;\mathrm\pi\times\mathrm r^2$$
Trong đó:
- là bán kính của mặt đáy
- là số Pi (khoảng 3.14159)
Diện tích toàn phần
Diện tích toàn phần hình trụ (S_tp) là diện tích bao gồm cả diện tích xung quanh và diện tích hai mặt đáy của hình trụ.
Diện tích toàn phần hình trụ được tính theo công thức
$$S_{tp}=2\pi\times r²+2\pi\times r\times h$$
Thế tích hình trụ là gì?
Thể tích hình trụ là thể tích của không gian giới hạn bởi mặt xung quanh và hai mặt đáy của hình trụ.
Công thức tính thể tích hình trụ:
$$V\;=\;\pi\times r²\times h$$
Trong đó: V là thể tích hình trụ (đơn vị: cm³, m³,…)
Ứng dụng của hình trụ trong thực tế
Với những kiến thức về hình trụ đã được trình bày ở trên, chúng ta có thể hiểu rõ hơn về các ứng dụng của nó trong thực tế. Các công trình kiến trúc thường sử dụng hình trụ để tạo ra các cột, tháp hay mái vòm. Ví dụ như Tháp Eiffel tại Pháp, đây là một trong những công trình nổi tiếng được xây dựng từ những hình trụ thép.
Hình trụ cũng được sử dụng để tạo ra các sản phẩm như bình nước, ống dẫn, hộp đựng và các thiết bị khác. Hình trụ còn được áp dụng trong khoa học và công nghệ để tạo ra các đường ống dẫn, đường hầm hay các mô hình máy móc.
Ngoài ra, hình trụ còn có vai trò quan trọng trong việc giải các bài toán tính toán diện tích và thể tích. Điều này còn được mở rộng sang việc giải các bài toán liên quan đến hình lăng trụ, hình nón tròn, hình nón vuông, hình hộp chữ nhật và nhiều loại hình khác. Vì vậy, hiểu rõ về hình trụ là cần thiết để có thể áp dụng vào các bài toán toán học và thực tế.
Các dạng bài tập về hình trụ
Để kiểm tra kiến thức về hình trụ, hãy cùng xem qua một số dạng bài tập phổ biến và cách giải của chúng.
Bài tập 1: Tính diện tích xung quanh và diện tích toàn phần của hình trụ
Yêu cầu: Cho hình trụ có bán kính đáy R = 5 cm, chiều cao h = 10 cm và chiều dài các cạnh bên l = 12 cm. Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
Giải: Để tính diện tích xung quanh và diện tích toàn phần, ta sử dụng các công thức đã trình bày ở trên. Diện tích xung quanh: $$Sxq = 2\pi Rh = 2 \cdot 3,14 \cdot 5 cm \cdot 10 cm = 314 cm^2$$ Diện tích toàn phần: $$Stp = Sxq + S_ = 314 cm^2 + (3,14 \cdot 5 cm)^2 = 439 cm^2$$
Vậy, diện tích xung quanh của hình trụ là 314 cm2 và diện tích toàn phần là 439 cm2.
Bài tập 2: Tính thể tích của hình trụ
Yêu cầu: Cho hình trụ có bán kính đáy R = 3 m và chiều cao h = 8 m. Tính thể tích của hình trụ.
Giải: Để tính thể tích của hình trụ, ta sử dụng công thức $$V = \pi R^2 \cdot h$$. Thay vào giá trị đã cho, ta có: $$V = 3,14 \cdot (3 m)^2 \cdot 8 m = 226,08 m^3$$
Vậy, thể tích của hình trụ là 226,08 m3.
Bài tập 3: Tìm chiều cao của hình trụ
Yêu cầu: Cho hình trụ có diện tích xung quanh là 88 cm2 và bán kính đáy là 4 cm. Tính chiều cao của hình trụ.
Giải: Để tìm chiều cao của hình trụ, ta sử dụng công thức $$Sxq = 2\pi Rh$$. Thay vào giá trị đã cho, ta có: $$88 cm^2 = 2 \cdot 3,14 \cdot 4 cm \cdot h$$ $$\Rightarrow h = 88 cm^2 / (2 \cdot 3,14 \cdot 4 cm) = 3,5 cm$$
Vậy, chiều cao của hình trụ là 3,5 cm.
Kết luận
Vậy hình trụ là gì? Đây là một khái niệm quan trọng trong toán học và hình học không gian. Chúng ta có thể tính được diện tích xung quanh, diện tích toàn phần và thể tích của hình trụ bằng các công thức tương ứng. Hình trụ còn được áp dụng rộng rãi trong các công trình kiến trúc, sản phẩm công nghiệp và trong giải các bài toán tính toán.




