Diện tích hình tứ diện: Công thức và các bài tập hướng dẫn chi tiết

Diện tích hình tứ diện là một thành phần quan trọng trong hình học không gian, được sử dụng để tính toán thể tích, trọng tâm và nhiều yếu tố khác liên quan đến hình tứ diện. Cùng tìm hiểu về công thức và các ví dụ minh họa cụ thể trong bài viết này.

Công thức tính diện tích hình tứ diện

Diện tích hình tứ diện được tính bằng tổng diện tích của bốn mặt của nó.

Để tính diện tích toàn phần hình tứ diện, ta cần biết diện tích của mỗi mặt. Trong đó, diện tích của mặt thứ nhất được ký hiệu là S1, mặt thứ hai là S2, mặt thứ ba là S3 và mặt thứ tư là S4.

Với các giá trị này, ta có công thức tính diện tích tổng quát của hình tứ diện:

$$S=S1+S2+S3+S4$$

Công thức này cho phép tính diện tích của bất kỳ hình tứ diện nào, dù có kích thước và hình dạng khác nhau.

Nếu bạn chưa rõ hình tứ diện là gì, hãy tìm hiểu trước khi tiếp tục với bài viết này.

Diện tích khối tứ diện đều 

Với tính chất các mặt trong hình đều bằng nhau của hình tứ diện đều, ta có thể rút ra công thức diện tích hình tứ diện đều như sau: 

$$Std=4\times Sm$$

Trong đó:

• Std: Diện tích tứ diện.
• Sm: Diện tích một mặt của tứ diện.

Ngoài ra, để tính được diện tích của hình tứ diện đều, ta cũng cần biết diện tích mỗi mặt với công thức: 

$$Smặt=\frac{a^2\sqrt3}4$$

Trong đó:

• Smặt: Diện tích 1 mặt của hình tứ diện
• a: Độ dài cạnh của tứ diện đều 

Ứng dụng của diện tích khối tứ diện trong thực tế

Việc tính toán diện tích của tứ diện không chỉ thỏa mãn sự tò mò toán học mà còn mở ra những ứng dụng thú vị trong đời sống thực tế.

Thiết kế kỹ thuật

Diện tích khối tứ diện là một yếu tố quan trọng trong việc thiết kế các cấu trúc xây dựng, máy móc và thiết bị. Khi tính toán diện tích của các mặt, chúng ta có thể dự đoán được khả năng chịu tải và hiệu quả sử dụng vật liệu. Điều này giúp cho việc thiết kế trở nên chính xác và an toàn hơn.

Hóa học

Trong hóa học, hình tứ diện được sử dụng để mô tả cấu trúc của các phân tử. Diện tích của các mặt có thể được sử dụng để phân tích các tương tác giữa các phân tử và đưa ra những dự đoán về tính chất và hoạt động của chúng.

Lý thuyết đồ thị

Hình tứ diện có thể được sử dụng để biểu diễn các mạng lưới kết nối trong lý thuyết đồ thị. Diện tích của các mặt có thể đại diện cho cường độ của các mối quan hệ giữa các nút trong mạng, giúp cho việc phân tích và nghiên cứu các dữ liệu đồ thị trở nên dễ dàng hơn.

Như đã đề cập ở trên, diện tích toàn phần của hình tứ diện là một công thức quan trọng trong hình học không gian và được ứng dụng trong nhiều lĩnh vực khác nhau. Bên cạnh việc tính toán diện tích khối tứ diện, thể tích hình tứ diện cũng là công thức được áp dụng nhiều trong các mảng khác nhau.

Bài tập ví dụ và hướng dẫn giải

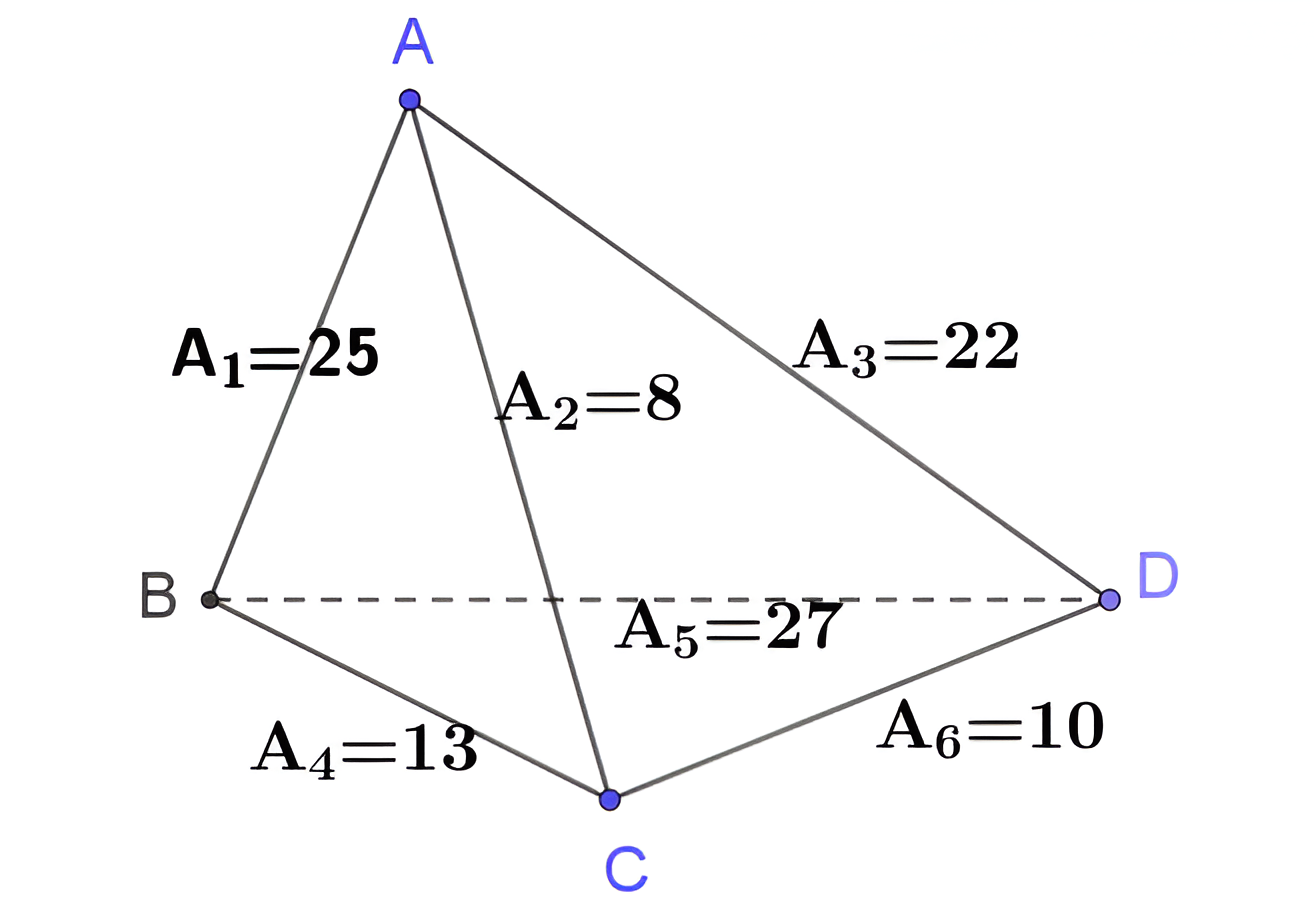
Đề bài 1

Cho hình tứ diện ABCD đều có cạnh a = 2cm. Tính diện tích tứ diện ABCD.

Lời giải:

Bước 1: Tính diện tích một mặt của tứ diện đều.

Công thức tính diện tích một mặt của tứ diện đều:

$$Sm=\frac{a^2\sqrt3}4$$

Thay a = 2cm vào công thức, ta được:

$$Sm=\frac{2^2\sqrt3}4=\sqrt3(cm²)$$

Bước 2: Tính diện tích tứ diện.

Công thức tính diện tích tứ diện đều:

$$Std=4\times Sm$$

Thay Sm = √3 (cm²) vào công thức, ta được:

$$Std=4\times\sqrt3=4\sqrt3(cm^2)$$

Vậy diện tích tứ diện ABCD đều là 4√3 cm².

Đề bài 2

Cho hình tứ diện ABCD có AB = 3cm, AC = 4cm, AD = 5cm, BC = 6cm, CD = 7cm và DA = 8cm. Tính diện tích tứ diện ABCD.

Lời giải:

Bước 1: Xác định loại tứ diện.

Dựa vào độ dài các cạnh, ta có thể thấy tứ diện ABCD không phải là tứ diện đều và cũng không phải là tứ diện vuông.

Bước 2: Tính diện tích các mặt của tứ diện.

• Diện tích mặt ABD:

Sử dụng công thức Heron để tính diện tích tam giác ABD:

$$S_{ABD}=\sqrt{s\times(s-AB)\times(s-AC)\times(s-AD)}$$

Trong đó, s là nửa chu vi tam giác ABD:

$$s=\frac{AB+AC+AD}2=\frac{3+4+5}2=6(cm)$$

Thay s = 6cm, AB = 3cm, AC = 4cm và AD = 5cm vào công thức, ta được:

$$S_{ABD}=\sqrt{6\times(6-3)\times(6-4)\times(6-5)}=6\sqrt3(cm²)$$

• Diện tích mặt ACD:

Tương tự, sử dụng công thức Heron để tính diện tích tam giác ACD:

$$S_{ACD}=\sqrt{s\times(s-AC)\times(s-AC)\times(s-CD)}$$

Trong đó, s là nửa chu vi tam giác ACD:

$$s=\frac{AC+AD+CD}2=\frac{4+5+7}2=8(cm)$$

Thay s = 8cm, AC = 4cm, AD = 5cm và CD = 7cm vào công thức, ta được:

$$S_{ACD}=\sqrt{8\times(8-4)\times(8-5)\times(8-7)}=4\sqrt5(cm²)$$

• Diện tích mặt BCD:

Tương tự, sử dụng công thức Heron để tính diện tích tam giác BCD:

$$S_{BCD}=\sqrt{s\times(s-BC)\times(s-CD)\times(s-BD)}$$

Trong đó, s là nửa chu vi tam giác BCD:

$$s=\frac{BC+CD+BD}2=\frac{6+7+8}2=10.5(cm)$$

Thay s = 10.5cm, BC = 6cm, CD = 7cm và BD = 8cm vào công thức, ta được:

S_BCD = √10.5(10.5 – 6)(10.5 – 7)(10.5 – 8) = 21√3 (cm²)

$$S_{BCD}=\sqrt{10.5\times(10.5-6)\times(10.5-7)\times(10.5-8)}=21\sqrt3(cm²)$$

Bước 3: Tính diện tích tứ diện.

Diện tích tứ diện ABCD bằng tổng diện tích các mặt của nó:

$$S_{td}=S_{ABD}+S_{ACD}+S_{BCD}=6\sqrt3+4\sqrt5+21\sqrt3=31\sqrt3(cm²)$$

Vậy diện tích tứ diện ABCD là 31√3 cm².

Kết luận

Trong bài viết này, chúng ta đã tìm hiểu về khái niệm diện tích hình tứ diện, cũng như trường hợp đặc biệt của hình tứ diện đều. Chúng ta cũng thấy rằng diện tích khối tứ diện không chỉ là một khái niệm lý thuyết mà còn được ứng dụng rộng rãi trong thực tế, từ thiết kế kỹ thuật đến lý thuyết đồ thị.