Khối nón là một phần kiến thức quan trọng trong chương trình toán hình không gian tại THPT. Vậy hình nón là gì? Trong bài viết dưới đây, chúng tôi sẽ giải thích chi tiết hơn về định nghĩa của hình nón, tính chất, công thức cũng như các dạng bài tập liên quan đến khối nón.
Định nghĩa khối nón tròn xoay
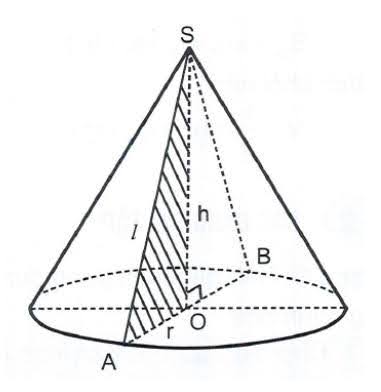
Cho tam giác SOB vuông tại O. Xoay tam giác này một góc 360 độ quanh cạnh SO ta được một hình nón tròn xoay có đường sinh SB, bán kính OB và đường cao SO.
Khi đó, hình nón là hình được tạo ra khi quay một tam giác vuông quanh một cạnh góc vuông cố định của nó.
#3 dạng hình nón thường gặp
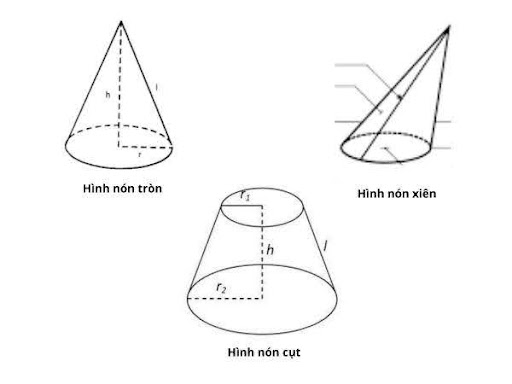
Có 3 dạng khối nón hay hình nón thường gặp đó là: Khôi nón tròn xoay, khối nón cụt và khối nón xiên.
- Khối nón tròn xoay: Được tạo thành bằng việc xoay tam giác vuông một góc 360 độ quanh trục là một cạnh góc vuông của nó. Khối nón tròn xoay bao gồm hình nón được tạo ra và phần không gian bên trong hình nón đó.
- Khối nón cụt: Là phần còn lại của khối nón tròn xoay sau khi cắt đỉnh bởi một mặt bằng song song với mặt phẳng đáy. Khối nón cụt có đáy là 2 hình tròn có bán kính khác nhau. Đường thẳng nối hai tâm của hai hình tròn là trục đối xứng của khối nón cụt.
- Khối nón xiên: Là khối nón có đỉnh nối với tâm của mặt đáy không vuông góc với mặt phẳng đáy.
Tính chất của khối nón là gì?
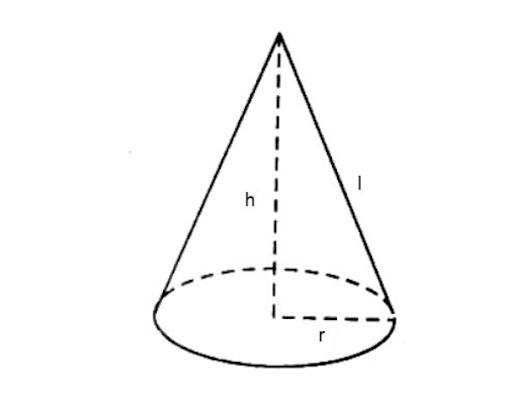
Trong chương trình học THPT, bạn sẽ gặp chủ yếu dạng toán liên quan đến khối nón tròn xoay. Có 4 đại lượng liên quan đến hình nón tròn xoay mà bạn cần nắm được bao gồm:
- O: Đỉnh của hình nón.
- R: Bán kính của đường tròn đáy.
- h: Đường cao của hình nón, là khoảng cách từ đỉnh đến tâm của hình tròn đáy.
- l: Đường sinh hình nón, là khoảng cách từ đỉnh đến một điểm bất kỳ trên đường tròn đáy.
Các tính chất cơ bản của khối nón
- Đáy của hình nón là một hình tròn.
- Hình nón rất đặc biệt bởi nó không có bất cứ cạnh nào.
- Thiết diện của hình nón:
+ Khi cắt hình nón bởi một mặt phẳng vuông góc với trục, thiết diện thu được là một hình tròn.
+ Khi cắt hình nón bởi một mặt phẳng đi qua đỉnh, thiết diện thu được là một tam giác cân tại đỉnh.
+ Khi cắt khối nón bởi một mặt phẳng song song với đường sinh, thiết diện thu được là một Hypepol.
Mở rộng thêm với khối nón cụt
- Khi cắt khối nón cụt bởi một mặt phẳng vuông góc với trục, thiết diện thu được là một hình tròn.
- Khi cắt khối nón cụt bởi một mặt phẳng song song với đường sinh, thiết diện thu được là một hình thang cân.
Mở rộng thêm với khối nón xiên
- Khi cắt khối nón xiên bởi một mặt phẳng đi qua đỉnh, thiết diện là hình tam giác cân tại đỉnh.
Công thức tính khối nón tròn xoay
Sau khi tìm hiểu khối nón là gì, các công thức liên quan đến hình nón tròn xoay rất quan trọng.
Công thức tính diện tích hình nón
Diện tích khối nón toàn phần = Diện tích xung quanh hình nón + Diện tích đáy của hình nón, hay:
Trong đó:
- Diện tích xung quanh hình nón là phần diện tích được tạo bởi việc quay đường sinh quanh trục.
- Diện tích đáy khối nón là một hình tròn.
Diện tích xung quanh của hình nón được tính như sau:
Trong đó:
- r là bán kính đáy của hình nón.
- l là đường sinh của hình nón.
Diện tích đáy hình nón được tính như sau:
Suy ra công thức tính diện tích toàn phần của hình nón:
Chú ý: Áp dụng định lý Py-ta-go ta có công thức tính đường sinh l = r2+ h2. Bạn cố thể linh hoạt áp dụng công thức này để tính diện tích khối nón.
Chu vi đáy hình nón hay còn gọi là công thức chu vi hình nón
Chu vi của hình nón thường được hiểu là chu vi của đáy khối nón. Đáy của hình nón là một hình tròn, do đó, chu vi của hình nón chính là chu vi của đường tròn đáy.
Đối với khối nón tròn xoay hay khối nón xiên, chu vi khối nón được ký hiệu là C và tính theo công thức như sau:
Trong đó:
- là số Pi, xấp xỉ bằng 3,14.
- r là bán kính đáy của khối nón.
- d là đường kính của đáy khối nón.
Đối với hình nón cụt sẽ có hai mặt đáy là hai hình tròn song song với bán kính khác nhau. Chu vi của hình nón cụt có thể hiểu là tổng chu vi của hai đáy.
>>> Xem thêm: Diện tích hình nón: Công thức và các mẹo giải bài tập nhanh
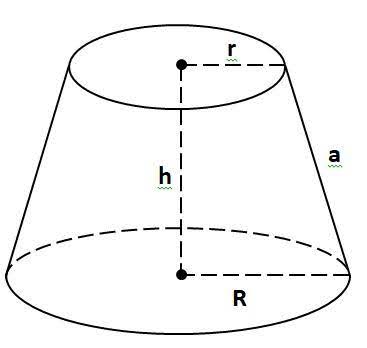
Nếu bán kính của đáy lớn là R và bán kính của đáy nhỏ là r, chu vi của hình nón cụt sẽ là tổng chu vi của hai đường tròn đáy, được tính theo công thức:
Trong đó:
- R là bán kính của đáy lớn
- r là bán kính của đáy nhỏ
- là hằng số Pi (khoảng 3.14159)
Ngoài ra, nếu D là bán kính của đáy lớn, d là bán kính của đáy nhỏ thì chu vi của hình nón cụt được tính theo công thức:
Trong đó:
- D là bán kính của đáy lớn
- D là bán kính của đáy nhỏ
- là hằng số Pi (khoảng 3.14159)
Công thức tính thể tích hình nón
Khối nón là hình nón và phần không gian bên trong hình nón. Hình nón được tạo thành bởi một đường thẳng (gọi là đường sinh) quay quanh một trục cố định và một mặt phẳng hình tròn (gọi là mặt đáy). Đường thẳng nối từ đỉnh xuống đáy và vuông góc với mặt phẳng đáy được gọi là chiều cao của khối nón.
Công thức thể tích khối nón được tính như sau:
Trong đó:
- V là thể tích khối nón (đơn vị m3, cm3,…)
- S là diện tích mặt đáy (đơn vị m2, cm2,…)
Công thức thể tích khối nón tròn xoay
Khối nón tròn xoay là khối nón mà đỉnh của nó được nối vuông góc với tâm của mặt đáy. Thể tích (V) của khối nón tròn xoay được tính bằng công thức:
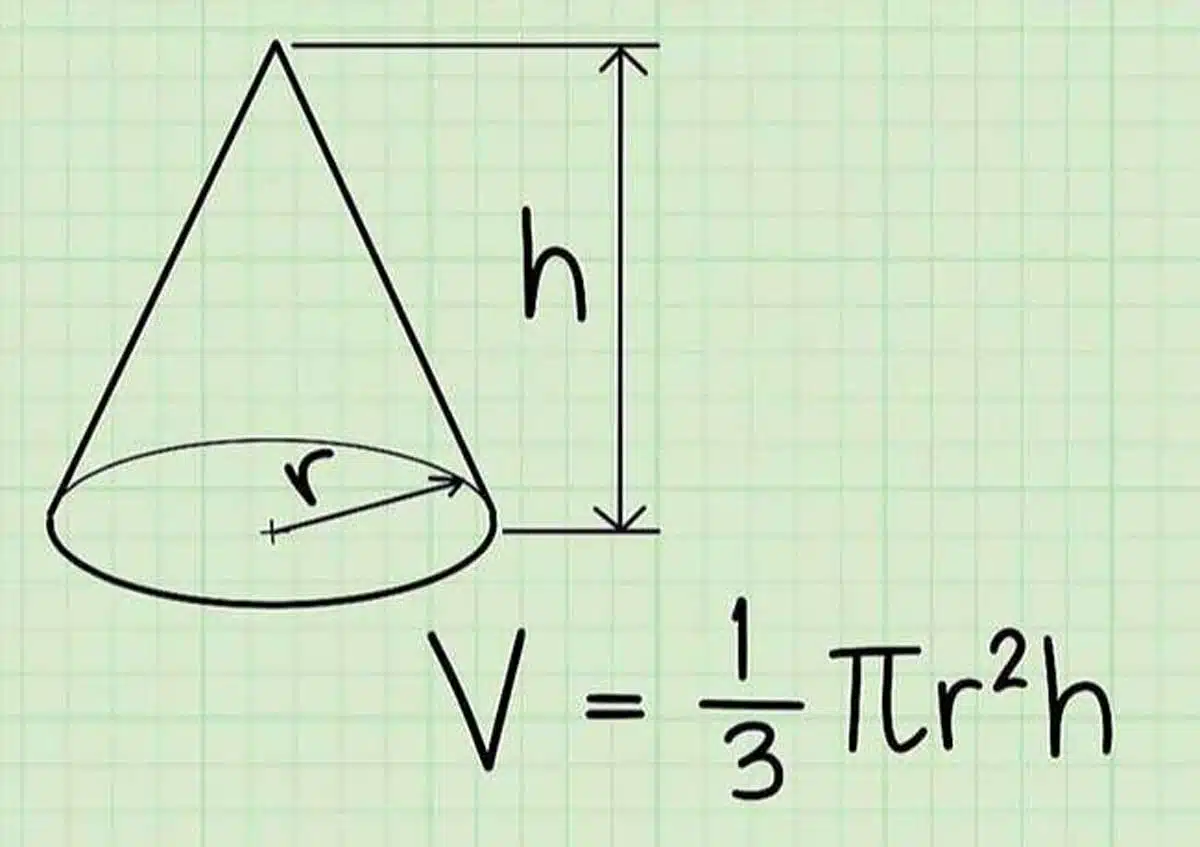
Trong đó:
- V: Thể tích (đơn vị m3, cm3,…)
- π: Số pi (xấp xỉ 3.14159)
- r: Bán kính mặt đáy nón (đơn vị m, cm,…)
- h: Chiều cao của nón (đơn vị m, cm,…)
>> Xem thêm: Diện tích hình nón: Công thức và các mẹo giải bài tập nhanh
Công thức tính thể tích khối nón cụt
Khối nón cụt là khối nón được tạo thành bởi hai mặt phẳng song song cắt một khối nón tròn xoay. Hai mặt phẳng cắt này gọi là hai mặt đáy của nón cụt. Chiều cao của nón cụt là khoảng cách giữa hai mặt đáy. Đường sinh là đoạn thẳng nối một điểm trên mặt đáy này với một điểm trên mặt đáy kia.
Cách tính thể tích hình nón cụt được trình bày qua công thức:
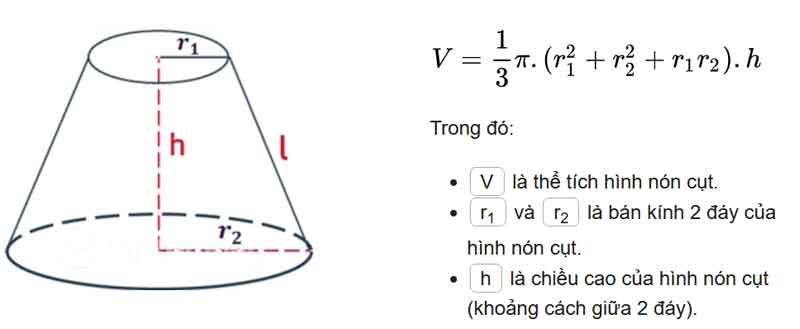
Trong đó:
- V: Thể tích (đơn vị m3, cm3,…)
- π: Số pi (xấp xỉ 3.14159)
- h: Chiều cao của nón cụt (đơn vị m, cm,…)
- R: Bán kính mặt đáy lớn của nón cụt (đơn vị m, cm,…)
- r: Bán kính mặt đáy nhỏ của nón cụt (đơn vị m, cm,…)
Công thức tính thể tích khối nón xiên
Khối nón xiên là khối nón mà đỉnh của nó không được nối vuông góc với tâm của hình tròn đáy. Trục của hình nón xiên không trùng với đường vuông góc tâm hình tròn đáy.
Thể tích (V) của khối nón xiên được tính bằng công thức:
Trong đó:
- V: Thể tích (đơn vị m3, cm3,…)
- π: Số pi (xấp xỉ 3.14159)
- r: Bán kính mặt đáy của nón xiên (đơn vị m, cm,…)
- h: Chiều cao của khối nón xiên (đơn vị m, cm,…)
Ứng dụng của khối nón trong thực tế
Trong thực tế, ứng dụng của khối nón là gì? Hình nón là một trong những hình cơ bản trong hình học không gian, có nhiều ứng dụng trong thực tế như:
- Kiến trúc và xây dựng: Hình nón được sử dụng để thiết kế lên mái vòm, tháp, … cùng nhiều công trình độc đáo khác.
- Trong công nghiệp và sản xuất: Hình nón được sử dụng trong các phễu để dẫn hướng chất lỏng hoặc vật liệu dạng hạt.
- Trong giao thông: Hình nón được ứng dụng làm cọc tiêu giao thông, điều tiết giao thông và cảnh báo người lái xe về các khu vực nguy hiểm hoặc đang thi công.
- Trong nghệ thuật và thiết kế: Hình nón được sử dụng làm các chi tiết trang trí, tạo điểm nhân như đèn treo, hoặc các tác phẩm hình nón.
- Trong khoa học vũ trụ: Đầu mũi của các tên lửa hoặc tàu vũ trụ thường có hình nón để giảm lực cản khi bay trong không gian.
- Trong giáo dục: Hình nón là một phần kiến thức quan trọng trong chương trình giáo dục THPT QG. Nắm vững kiến thức về hình nón sẽ giúp bạn giải quyết các bài toán liên quan.
>> Xem thêm: Hình cầu là gì? Tính chất, công thức quan trọng về hình cầu
Trên đây là chia sẻ của chúng tôi về hình nón là gì, các công thức liên quan đến hình nón cùng các bài tập vận dụng. Đừng quên theo dõi Hocthenao.Vn để khám phá thêm nhiều dạng bài hay về khối nón nhé.




