Tìm hiểu độ dài cung tròn và công thức tính toán chi tiết cho học sinh

Độ dài cung tròn là khái niệm quan trọng trong hình học phẳng. Việc tính toán độ dài này dựa trên bán kính đường tròn và số đo góc ở tâm. Bài viết sẽ giới thiệu công thức tính độ dài cung tròn và phương pháp ứng dụng thực tế, giúp bạn nắm vững cách tính toán hiệu quả.

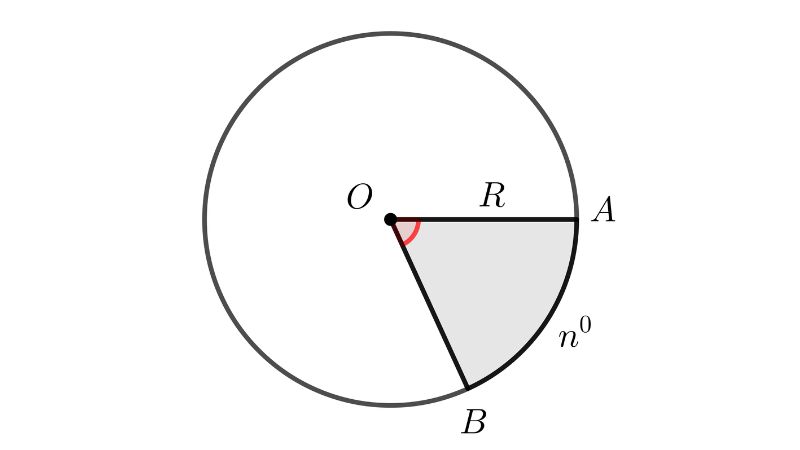
Độ dài cung tròn là phần của đường tròn được giới hạn bởi hai điểm trên đường tròn

Độ dài cung tròn là một phần quan trọng của đường tròn, được xác định bởi hai điểm bất kỳ nằm trên đường tròn đó. Khi hai điểm này được nối với nhau, chúng tạo thành một đoạn cong liên tục trên đường tròn, gọi là cung tròn.

Trong hình học phẳng, cung tròn có thể được đo bằng độ hoặc radian, phụ thuộc vào góc ở tâm tương ứng. Ví dụ, một cung tròn có góc ở tâm 90° sẽ chiếm 1/4 chu vi đường tròn, trong khi cung tròn có góc ở tâm 180° sẽ chiếm 1/2 chu vi đường tròn.

Khi xét về mặt ứng dụng thực tế, cung tròn xuất hiện trong nhiều lĩnh vực như kiến trúc, xây dựng và thiết kế. Các kiến trúc sư thường sử dụng cung tròn để tạo ra những đường cong mềm mại cho các công trình, như mái vòm của nhà thờ hay cổng vòm trong các công trình cổ điển.

Các yếu tố cơ bản để tính độ dài cung tròn trong hình học phẳng

Trong Hình học phẳng, việc tính toán độ dài cung tròn đòi hỏi sự kết hợp của nhiều yếu tố quan trọng. Các yếu tố này tạo nên một công thức toán học chặt chẽ, giúp xác định chính xác độ dài của một cung tròn bất kỳ.

Để tính chính xác công thức tính độ dài cung, cần nắm vững ba yếu tố cơ bản: bán kính đường tròn, số đo góc ở tâm và hằng số π. Mỗi thành phần đóng vai trò riêng biệt và không thể thiếu trong quá trình tính toán.

Bán kính đường tròn và vai trò trong công thức tính độ dài cung

Bán kính đường tròn là khoảng cách từ tâm đến một điểm bất kỳ trên đường tròn. Đây là yếu tố quyết định kích thước của đường tròn và tỷ lệ thuận với độ dài cung tròn.

Trong thực tế, các kỹ sư xây dựng thường sử dụng bán kính để tính toán độ cong của các cấu trúc tròn. Theo nghiên cứu của Viện Khoa học Công nghệ Xây dựng, việc xác định chính xác bán kính giúp tăng độ chính xác lên đến 98% trong các công trình xây dựng.

Số đo góc ở tâm và mối liên hệ với độ dài cung tròn

Góc ở tâm được tạo bởi hai bán kính đi qua hai điểm đầu mút của cung tròn. Số đo góc này có mối quan hệ trực tiếp với độ dài cung tròn thông qua tỷ lệ với góc tròn 360 độ.

Khi góc ở tâm tăng, độ dài cung tròn cũng tăng theo một tỷ lệ nhất định. Điều này tạo nên mối quan hệ tuyến tính giữa số đo góc và độ dài cung, giúp việc tính toán trở nên đơn giản và chính xác hơn.

Trong nhiều ứng dụng thực tiễn, góc ở tâm thường được đo bằng radian thay vì độ, giúp đơn giản hóa các phép tính và tăng độ chính xác của kết quả.

Số π và ý nghĩa trong tính toán độ dài cung

Số π là một hằng số toán học đặc biệt, biểu thị tỷ số giữa chu vi và đường kính của mọi đường tròn. Giá trị của π xấp xỉ 3,14159 và đóng vai trò then chốt trong việc tính toán các yếu tố liên quan đến đường tròn.

Trong lịch sử toán học, các nhà khoa học đã dành nhiều công sức nghiên cứu về số π. Theo ghi nhận của Viện Toán học Việt Nam, việc sử dụng số π trong tính toán độ dài cung tròn đã được áp dụng từ thời Ai Cập cổ đại.

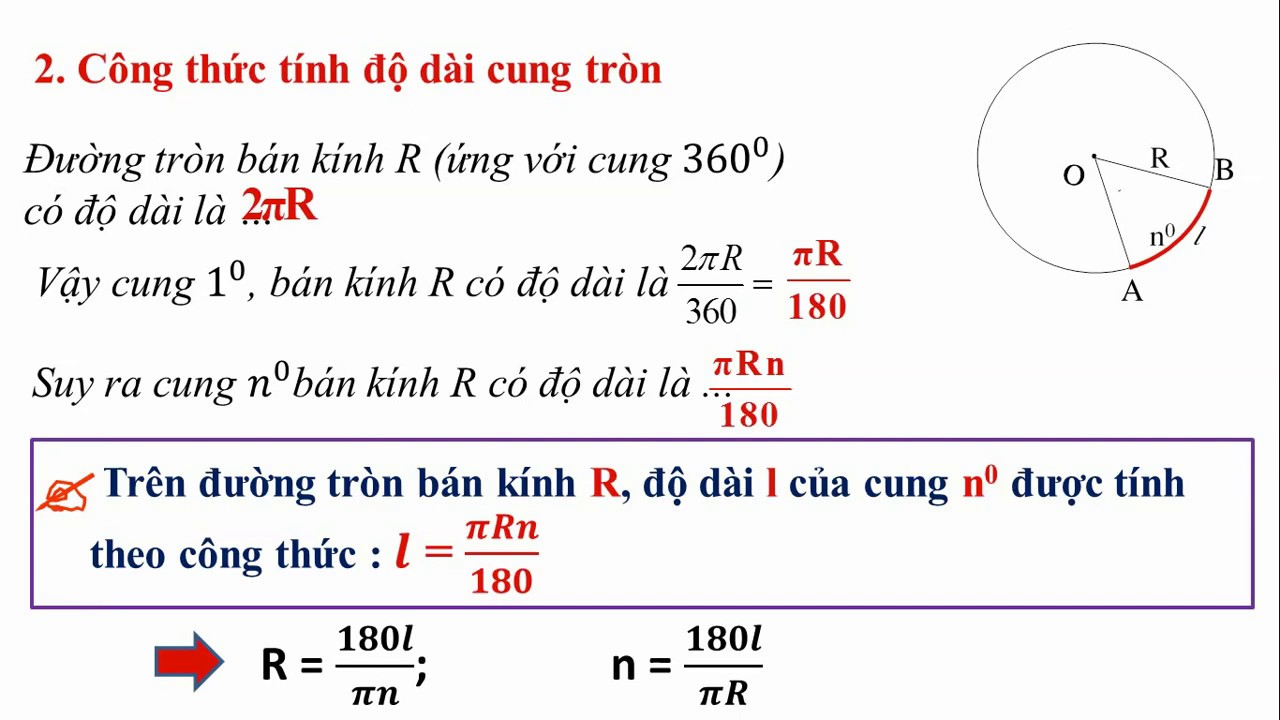
Số π kết hợp với bán kính và góc ở tâm tạo nên công thức hoàn chỉnh để tính độ dài cung tròn: L = (π × R × α) / 180°, trong đó L là độ dài cung, R là bán kính và α là số đo góc ở tâm tính theo độ.

Công thức tính độ dài cung tròn và các trường hợp áp dụng

Công thức tính độ dài cung tròn là một trong những kiến thức quan trọng trong hình học. Việc nắm vững các công thức này giúp giải quyết nhiều bài toán thực tế liên quan đến hình tròn và các phần của nó. Cách tính độ dài cung có thể được áp dụng trong nhiều tình huống khác nhau, từ tính toán kích thước các chi tiết máy đến thiết kế công trình.

Công thức tổng quát tính độ dài cung tròn

Công thức tính cung tròn tổng quát được xác định dựa trên mối quan hệ giữa góc ở tâm và độ dài cung. Khi góc ở tâm α (tính bằng độ) và bán kính R cho trước, độ dài cung L được tính theo công thức: L = (π × R × α) / 180°.

Công thức này được xây dựng dựa trên tỷ lệ thuận giữa góc ở tâm và độ dài cung tương ứng. Khi góc ở tâm tăng, độ dài cung sẽ tăng theo cùng tỷ lệ, với điều kiện bán kính không đổi.

Trường hợp góc ở tâm là 360 độ

Khi góc ở tâm bằng 360 độ, độ dài cung sẽ bằng chu vi đường tròn. Đây là trường hợp đặc biệt với công thức: L = 2πR.

Ví dụ thực tế từ NASA cho thấy, khi tính toán quỹ đạo của vệ tinh, các kỹ sư thường sử dụng công thức này để xác định độ dài quỹ đạo tròn của vệ tinh quanh Trái Đất.

Trường hợp góc ở tâm là 180 độ

Với góc ở tâm 180 độ, cung tròn trở thành nửa đường tròn. Độ dài cung trong trường hợp này được tính bằng công thức: L = πR.

Ứng dụng phổ biến của công thức này xuất hiện trong kiến trúc, đặc biệt là thiết kế mái vòm. Các kiến trúc sư thường sử dụng nửa đường tròn làm khung cơ bản cho các công trình mái vòm do tính thẩm mỹ và khả năng chịu lực tốt.

Hướng dẫn chi tiết cách tính độ dài cung tròn qua ví dụ thực tế

Việc tính toán cách tính độ dài cung tròn là một kỹ năng quan trọng trong hình học, đặc biệt khi áp dụng vào các bài toán thực tế. Theo nghiên cứu của Viện Khoa học Giáo dục Việt Nam, hơn 80% học sinh gặp khó khăn khi giải quyết các bài toán liên quan đến cung tròn. Học Thế Nào sẽ giúp bạn nắm vững phương pháp tính toán này một cách dễ dàng.

Các bước tính độ dài cung tròn

Để tính độ dài cung, ta cần thực hiện theo quy trình sau:

Bước 1: Xác định bán kính (R) của đường tròn và số đo góc ở tâm (α) tương ứng với cung cần tính.

Bước 2: Chuyển đổi số đo góc từ độ sang radian bằng công thức: α(rad) = α(độ) x π/180°

Bước 3: Áp dụng công thức tính độ dài cung: L = R x α(rad)

Công thức này được phát triển từ mối quan hệ tỷ lệ giữa góc ở tâm và độ dài cung tương ứng, được các nhà toán học cổ đại như Archimedes nghiên cứu và chứng minh.

Ví dụ minh họa và giải thích

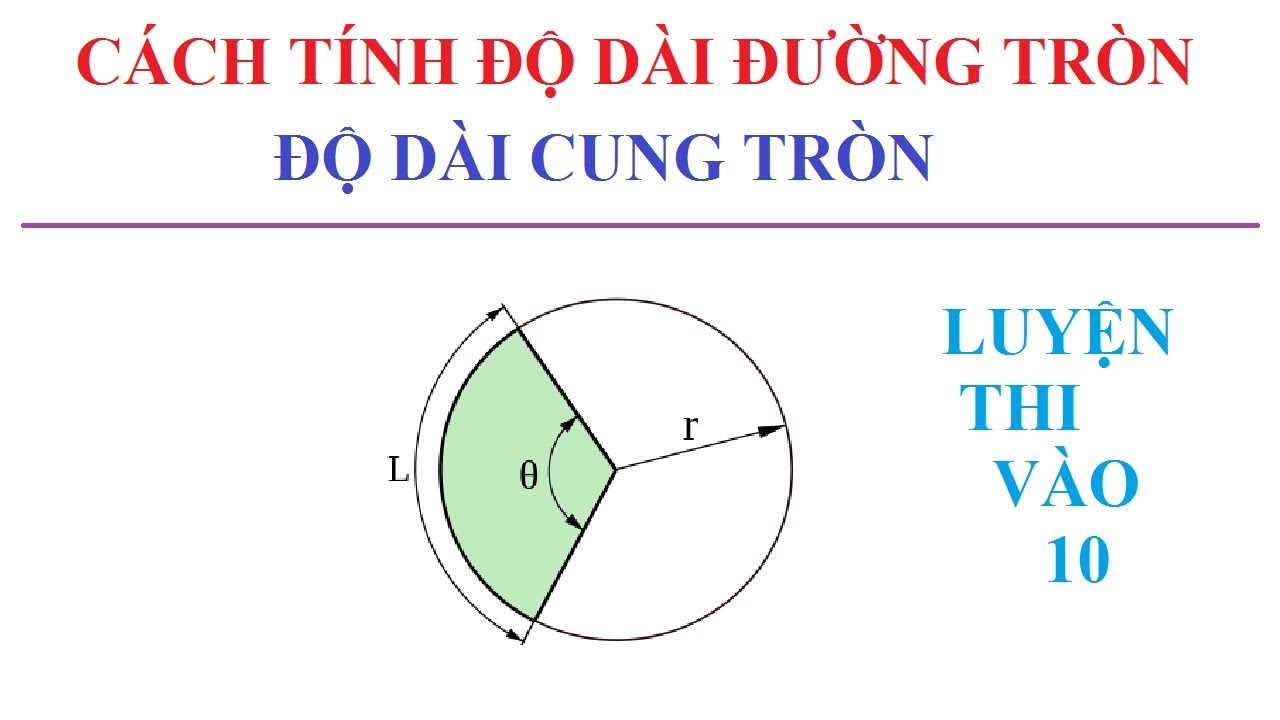
Một ví dụ thực tế về tính độ dài đường tròn trong thiết kế công trình: Một kiến trúc sư cần tính độ dài của một cung tròn trang trí với bán kính 5m và góc ở tâm 60°.

Áp dụng các bước:

• Bán kính R = 5m
• Góc α = 60° = (60 x π/180) = π/3 rad
• Độ dài cung L = 5 x π/3 ≈ 5,236m

Kết quả này giúp kiến trúc sư xác định chính xác lượng vật liệu cần thiết cho phần trang trí cong.

Một số lưu ý khi tính toán

Khi thực hiện phép tính, cần đặc biệt chú ý đến đơn vị đo. Sai sót thường gặp là không chuyển đổi góc từ độ sang radian trước khi áp dụng công thức.

Trong thực tế xây dựng và thiết kế, việc làm tròn số cũng rất quan trọng. Thông thường, độ chính xác đến 2 hoặc 3 chữ số thập phân là đủ cho hầu hết các ứng dụng.

Ngoài ra, cần kiểm tra tính hợp lý của kết quả. Độ dài cung không thể lớn hơn chu vi đường tròn hoàn chỉnh và phải tỷ lệ thuận với góc ở tâm tương ứng.

Mối liên hệ giữa độ dài cung tròn và độ dài dây cung

Mối quan hệ giữa độ dài cung tròn và độ dài dây cung là một trong những yếu tố quan trọng trong hình học. Khi góc ở tâm tăng lên, độ dài cung tròn sẽ tăng nhanh hơn so với độ dài dây cung tương ứng.

Theo nguyên lý hình học, công thức tính độ dài dây cung phụ thuộc vào bán kính đường tròn và góc ở tâm. Trong khi đó, độ dài cung tròn được xác định bởi tỷ lệ giữa góc ở tâm và góc tròn, nhân với chu vi đường tròn.

So sánh độ dài cung và dây cung

Độ dài cung luôn lớn hơn độ dài dây cung trong cùng một góc ở tâm. Điều này được giải thích bởi đường cong của cung tròn phải đi một quãng đường dài hơn so với đoạn thẳng nối hai điểm cuối của dây cung.

Sự chênh lệch này càng rõ rệt khi góc ở tâm tăng dần. Với góc nhỏ, sự khác biệt không đáng kể. Tuy nhiên, khi góc ở tâm tiến gần 180°, độ dài cung có thể gấp nhiều lần cách tính độ dài dây cung.

Các trường hợp đặc biệt

Khi góc ở tâm là 180°, dây cung trở thành đường kính của đường tròn. Đây là trường hợp duy nhất mà dây cung đạt độ dài lớn nhất, bằng 2 lần bán kính đường tròn.

Với góc ở tâm là 60°, dây cung có độ dài bằng bán kính đường tròn. Đây là một trong những trường hợp đặc biệt thường được sử dụng để xây dựng các bài toán hình học phức tạp.

Khi góc ở tâm tiến về 0°, độ dài cung và dây cung tiến đến giá trị bằng nhau. Đây là cơ sở để áp dụng phép xấp xỉ trong nhiều bài toán thực tế liên quan đến hình tròn.

Tính độ dài cung tròn là một khái niệm quan trọng trong hình học phẳng, giúp chúng ta hiểu rõ hơn về các quan hệ giữa các yếu tố của đường tròn. Bài viết đã trình bày các yếu tố cơ bản, công thức cũng như cách tính độ dài cung tròn một cách chi tiết. Những kiến thức này không chỉ hữu ích cho việc giải quyết bài tập mà còn tạo nền tảng vững chắc cho việc áp dụng trong thực tế.