Đồng quy là gì và các khái niệm cơ bản trong hình học phẳng

Đồng quy là gì? Khái niệm này liên quan mật thiết đến hình học phẳng và tính chất của các đường thẳng. Việc hiểu rõ khái niệm đồng quy giúp học sinh nắm vững kiến thức, áp dụng vào giải bài tập một cách hiệu quả. Hãy cùng khám phá những đặc điểm, định lý, và ứng dụng thực tiễn của đồng quy trong toán học.

Đồng quy là gì?

Đồng quy là hiện tượng các đường thẳng, đường cong hoặc các yếu tố hình học khác gặp nhau tại một điểm chung. Trong toán học, khái niệm này thường được sử dụng để mô tả sự hội tụ của nhiều đối tượng hình học về một vị trí xác định.

Trong hình học phẳng, đồng quy là j một khái niệm quan trọng thường xuất hiện trong các bài toán về đường thẳng, đường tròn và các hình phẳng khác. Khi các đường thẳng hoặc đường cong đồng quy, chúng tạo thành một điểm đặc biệt gọi là tâm đồng quy. Điểm này có thể nằm trong mặt phẳng hoặc ở vô cùng.

Ứng dụng của đồng quy không chỉ giới hạn trong toán học thuần túy mà còn xuất hiện trong nhiều lĩnh vực thực tiễn. Trong kiến trúc, các đường thẳng đồng quy được sử dụng để tạo hiệu ứng phối cảnh, giúp công trình có chiều sâu và tính thẩm mỹ cao. Trong nghệ thuật, kỹ thuật này được họa sĩ áp dụng để vẽ tranh phối cảnh một điểm, hai điểm hoặc ba điểm nhằm tạo cảm giác không gian ba chiều trên mặt phẳng hai chiều.

Các khái niệm cơ bản về đường thẳng và điểm đồng quy trong hình học

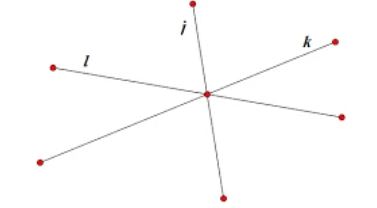
Trong toán hình học phẳng, khái niệm về đường thẳng đồng quy và điểm đồng quy đóng vai trò quan trọng trong việc nghiên cứu các tính chất hình học. Đường thẳng đồng quy là tập hợp các đường thẳng đi qua cùng một điểm. Điểm chung mà các đường thẳng cắt nhau được gọi là điểm đồng quy.

Đường đồng quy thường xuất hiện trong nhiều bài toán hình học và có ứng dụng rộng rãi trong thực tế. Ví dụ trong kiến trúc, các đường thẳng song song khi nhìn từ xa sẽ tạo thành các đường đồng quy hướng về một điểm ảo trên đường chân trời. Đây là nguyên lý cơ bản của phép chiếu phối cảnh được các họa sĩ và kiến trúc sư áp dụng.

Điểm đồng quy có vai trò đặc biệt quan trọng trong việc chứng minh các định lý hình học. Một số định lý nổi tiếng như định lý Ceva, định lý Menelaus đều liên quan đến tính chất đồng quy của các đường thẳng. Trong tam giác, trung tuyến, đường cao và phân giác trong tam giác đều có điểm đồng quy riêng với những tính chất đặc trưng.

Việc nắm vững các khái niệm về đường thẳng và điểm đồng quy giúp giải quyết nhiều bài toán phức tạp trong hình học. Đặc biệt trong các bài toán tìm tập hợp điểm, việc xác định điểm đồng quy thường là chìa khóa quan trọng dẫn đến lời giải.

Tính chất và định lý quan trọng về đồng quy trong hình học phẳng

Đồng quy là gì – khái niệm chỉ trạng thái khi ba hay nhiều đường thẳng cắt nhau tại một điểm. Trong hình học phẳng, tính chất đồng quy đóng vai trò quan trọng giúp chứng minh nhiều bài toán phức tạp. Các định nghĩa đồng quy thường gắn liền với các yếu tố đặc biệt trong tam giác như đường trung tuyến, đường cao và đường phân giác.

Các tính chất cơ bản của đường thẳng đồng quy

Khi ba đường thẳng đồng quy, chúng tạo thành các cặp góc đối đỉnh bằng nhau tại điểm đồng quy. Điều này giúp thiết lập mối quan hệ giữa các góc trong tam giác và các yếu tố khác.

Ngoài ra, nếu ba đường thẳng đồng quy, mọi đường thẳng cắt chúng sẽ tạo thành ba cặp điểm thẳng hàng. Tính chất này thường được áp dụng trong việc chứng minh các bài toán về tỉ số.

Định lý về điểm đồng quy của đường trung tuyến

Trong một tam giác, ba đường trung tuyến luôn đồng quy tại một điểm gọi là trọng tâm. Trọng tâm chia mỗi đường trung tuyến theo tỉ lệ 2:1, tính từ đỉnh tam giác.

Trọng tâm còn là tâm của hệ ba lực có cường độ bằng nhau đặt tại ba đỉnh của tam giác. Đây là một ứng dụng quan trọng trong vật lý và cơ học.

Định lý về điểm đồng quy của đường cao

Ba đường cao của tam giác luôn đồng quy tại một điểm gọi là trực tâm. Vị trí của trực tâm phụ thuộc vào loại tam giác:

Với tam giác nhọn, trực tâm nằm trong tam giác. Với tam giác tù, trực tâm nằm ngoài tam giác. Với tam giác vuông, trực tâm trùng với đỉnh góc vuông.

Định lý về điểm đồng quy của đường phân giác

Ba đường phân giác trong của tam giác luôn đồng quy tại một điểm gọi là tâm nội tiếp. Điểm này cách đều ba cạnh của tam giác và là tâm của đường tròn nội tiếp.

Tương tự, ba đường phân giác ngoài cũng đồng quy tại các điểm gọi là tâm ngoại tiếp. Mỗi tam giác có ba tâm ngoại tiếp, mỗi điểm là tâm của một đường tròn ngoại tiếp tiếp xúc với một cạnh của tam giác và phần kéo dài của hai cạnh còn lại.

Phương pháp giải các bài toán liên quan đến đồng quy

Để giải các bài toán về phương trình đồng quy, cần nắm vững các phương pháp và kỹ thuật cơ bản. Việc xác định điểm đồng quy đóng vai trò then chốt trong quá trình giải quyết bài toán.

Một trong những yếu tố quan trọng là hiểu rõ mối liên hệ giữa các đường thẳng và điểm đồng quy. Điều này liên quan mật thiết đến góc đồng vị là gì và các tính chất hình học cơ bản.

Việc áp dụng các công thức và định lý phù hợp sẽ giúp xác định chính xác vị trí điểm đồng quy. Đây là cơ sở để giải bài tập đồng quy một cách hiệu quả.

Các dạng bài tập thường gặp về đồng quy

Trong hình học phẳng, các bài toán về đồng quy là gì thường xuất hiện dưới nhiều dạng khác nhau. Việc phân loại và nắm vững đặc điểm của từng dạng sẽ giúp định hướng phương pháp giải phù hợp.

Dạng bài tập phổ biến nhất là chứng minh ba đường thẳng đồng quy. Bài toán này đòi hỏi vận dụng linh hoạt các kiến thức về góc, đường thẳng song song và định lý về góc.

Ngoài ra còn có các dạng bài tập về đồng quy của đường cao, đường trung tuyến và đường phân giác trong tam giác. Mỗi dạng bài có những đặc thù riêng và cần áp dụng các phương pháp giải phù hợp.

Phương pháp chứng minh đồng quy

Để chứng minh đồng quy, phương pháp thường dùng là chứng minh hai đường thẳng cắt nhau tại một điểm, sau đó chứng minh điểm đó nằm trên đường thẳng thứ ba.

Một cách tiếp cận khác là sử dụng phương pháp phản chứng. Giả sử các đường thẳng không đồng quy, từ đó tìm ra mâu thuẫn để kết luận các đường thẳng phải đồng quy.

Việc áp dụng các định lý về tam giác, đặc biệt là định lý về góc và đường thẳng song song, cũng là công cụ hữu hiệu trong chứng minh đồng quy.

Kỹ thuật xác định điểm đồng quy

Xác định điểm đồng quy đòi hỏi sự kết hợp giữa kiến thức hình học và kỹ năng tính toán. Việc sử dụng hệ trục tọa độ và phương trình đường thẳng là phương pháp hiệu quả.

Trong nhiều trường hợp, việc xác định điểm đồng quy có thể thực hiện thông qua tính chất đặc biệt của hình. Ví dụ như trọng tâm là điểm đồng quy của ba đường trung tuyến, trực tâm là điểm đồng quy của ba đường cao.

Kỹ thuật vẽ hình chính xác và quan sát các yếu tố đối xứng cũng giúp xác định nhanh vị trí điểm đồng quy. Điều này đặc biệt hữu ích khi giải các bài toán về đồng quy trong hình học sơ cấp.

Ứng dụng của tính chất đồng quy trong hình học và thực tiễn

Tính chất đồng quy là gì và ứng dụng của nó đã được chứng minh qua nhiều thế kỷ phát triển của toán học. Đây là một trong những tính chất quan trọng giúp giải quyết nhiều bài toán phức tạp trong hình học phẳng cũng như các ứng dụng thực tiễn.

Ứng dụng đồng quy được thể hiện rõ nét trong nhiều lĩnh vực, từ toán học thuần túy đến các ứng dụng thực tế trong kiến trúc và xây dựng. Việc hiểu và vận dụng đúng các nguyên lý của hình học đồng quy giúp tối ưu hóa thiết kế và nâng cao hiệu quả giải quyết vấn đề.

Ứng dụng trong giải toán hình học phẳng

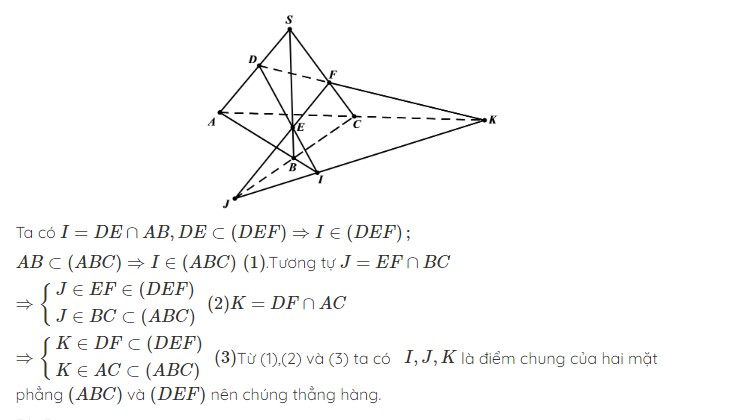
Trong giải toán hình học phẳng, tính chất đồng quy thường được áp dụng để chứng minh các điểm đặc biệt nằm trên cùng một đường thẳng. Phương pháp này giúp đơn giản hóa việc giải quyết các bài toán phức tạp về tam giác và tứ giác.

Một ví dụ điển hình là định lý Ceva, cho phép chứng minh ba đường thẳng đồng quy bằng cách sử dụng tỷ số các đoạn thẳng. Theo GS. Nguyễn Cảnh Toàn, việc áp dụng định lý này đã giúp giải quyết thành công nhiều bài toán Olympic quốc tế.

Ứng dụng trong thiết kế và xây dựng

Trong lĩnh vực kiến trúc, nguyên lý đồng quy được ứng dụng để tạo ra hiệu ứng thị giác ấn tượng. Các đường thẳng hội tụ về một điểm tạo cảm giác về chiều sâu và không gian ba chiều trên bề mặt phẳng.

Công ty kiến trúc Foster + Partners đã áp dụng nguyên lý này trong thiết kế trung tâm thương mại The Avenues ở Kuwait. Các đường nét kiến trúc được thiết kế hội tụ về một điểm, tạo ra không gian độc đáo và thu hút.

Việc ứng dụng tính chất đồng quy còn giúp tối ưu hóa cấu trúc chịu lực của công trình, đảm bảo tính thẩm mỹ và độ bền vững.

Ứng dụng trong các bài toán thực tế

Trong thực tế, tính chất đồng quy được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Từ thiết kế đồ họa, nơi các đường thẳng đồng quy tạo ra hiệu ứng phối cảnh ấn tượng, đến quy hoạch đô thị với việc bố trí các tuyến đường giao thông hợp lý.

Một ứng dụng quan trọng khác là trong lĩnh vực quang học, nơi các tia sáng hội tụ qua thấu kính được mô tả bằng các đường thẳng đồng quy. Nguyên lý này được sử dụng trong thiết kế camera, kính viễn vọng và các thiết bị quang học khác.

Các nhà khoa học tại Viện Vật lý Kỹ thuật đã ứng dụng tính chất này để phát triển hệ thống thu năng lượng mặt trời hiệu quả, với các tấm gương phản xạ được bố trí theo nguyên lý đồng quy để tập trung ánh sáng vào một điểm.

Trong hình học, đồng quy là gì là một khái niệm quan trọng giúp chúng ta hiểu về mối quan hệ giữa các đường thẳng và điểm trong không gian. Qua các tính chất và định lý liên quan đến đồng quy, bạn sẽ có cái nhìn rõ hơn về hệ thống hình học cũng như ứng dụng của nó trong giải toán. Việc nắm vững kiến thức này không chỉ giúp bạn trong việc học mà còn trong thực tiễn, từ thiết kế đến giải quyết các bài toán hàng ngày.