Góc đồng vị là gì và ứng dụng trong hình học phẳng dễ hiểu cho học sinh

Góc đồng vị là gì? Đây là một khái niệm quan trọng trong hình học cần được hiểu rõ. Hai góc đồng vị có cùng độ lớn và có vị trí nhất định trên hai đường thẳng song song. Nắm vững định nghĩa và tính chất sẽ giúp bạn giải quyết nhiều bài toán hình học dễ dàng hơn. Hãy cùng khám phá thêm về đặc điểm, cách nhận diện và ứng dụng của góc đồng vị trong học tập!

Góc đồng vị là gì?

Góc đồng vị là góc có số đo bằng nhau và cùng hướng quay, được tạo thành khi quay một góc ban đầu một số vòng tròn (có thể là số nguyên hoặc phân số). Khi một góc quay nhiều vòng, các vị trí trùng nhau của cạnh góc sẽ tạo thành các góc đồng vị.

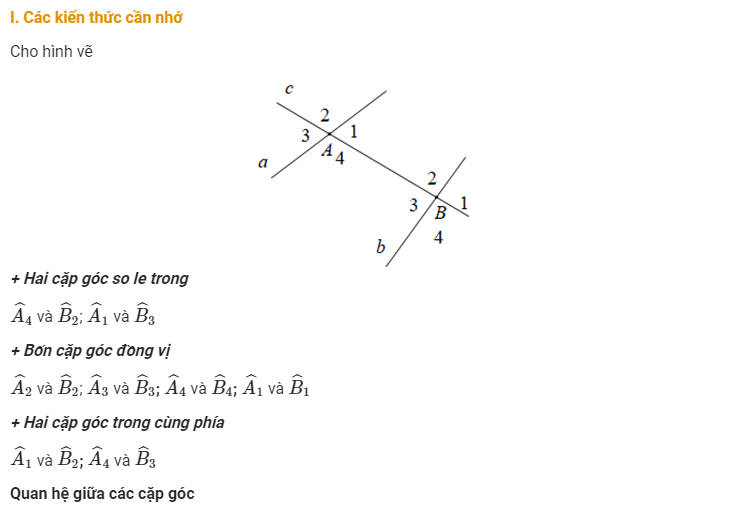
Trong toán học, góc đồng vị là gì có thể được hiểu qua công thức α + 360° × n, trong đó α là góc ban đầu và n là số nguyên. Ví dụ, góc 30° sẽ có các góc đồng vị là 390° (30° + 360°), 750° (30° + 360° × 2), -330° (30° – 360°). Các góc này tuy có số đo khác nhau nhưng đều cho cùng một vị trí của cạnh góc.

Việc xác định góc đồng vị có ý nghĩa quan trọng trong nhiều lĩnh vực như toán học, vật lý và kỹ thuật. Trong thực tế, góc đồng vị thường được ứng dụng trong các bài toán về chuyển động tròn, dao động tuần hoàn hay các hệ thống bánh răng. Ví dụ trong thiết kế động cơ, việc tính toán góc đồng vị giúp xác định chính xác vị trí của các chi tiết máy sau mỗi chu kỳ quay.

Đặc điểm nhận dạng và tính chất của góc đồng vị trong hình học phẳng

Hai góc đồng vị là hai góc có cùng số đo và cùng chiều quay khi đặt chồng khít hai đỉnh góc lên nhau. Trong hình học phẳng, góc đồng vị đóng vai trò quan trọng trong việc chứng minh các bài toán về góc và đường thẳng.

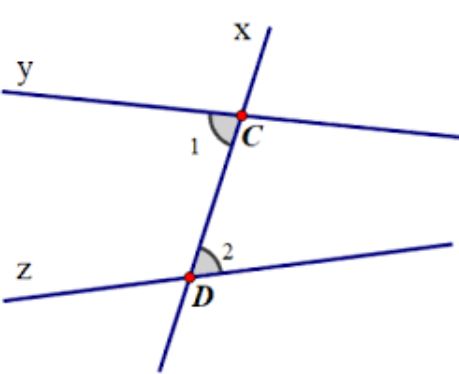
Góc đồng vị thường xuất hiện khi ta có hai đường thẳng song song bị cắt bởi một đường thẳng cắt. Khi đó, các cặp góc đồng vị sẽ được tạo thành ở các vị trí tương ứng. Tương tự như trung vị là gì, góc đồng vị cũng là một khái niệm cơ bản cần nắm vững trong hình học.

Cách nhận biết hai góc đồng vị trong hình học

Góc đồng vị có thể được nhận biết thông qua một số đặc điểm đặc trưng. Khi hai đường thẳng song song bị cắt bởi một đường thẳng, các góc tương ứng tạo thành sẽ là góc đồng vị.

Một cách khác để nhận biết là khi hai góc có cùng số đo và cùng chiều quay, nếu đặt chồng khít hai đỉnh góc thì hai cạnh của góc này sẽ trùng với hai cạnh của góc kia. Điều này giúp ta dễ dàng xác định được 2 góc đồng vị trong các bài toán hình học.

Các tính chất quan trọng của góc đồng vị

Góc đồng vị có nhiều tính chất quan trọng cần được nghiên cứu kỹ lưỡng. Các tính chất này được chia thành hai nhóm chính: tính chất về độ lớn và tính chất về vị trí tương đối.

Tính chất về độ lớn của góc đồng vị

Định nghĩa góc đồng vị cho thấy hai góc đồng vị luôn có số đo bằng nhau. Đây là tính chất cơ bản nhất và quan trọng nhất của góc đồng vị.

Khi hai đường thẳng song song bị cắt bởi một đường thẳng, các góc đồng vị tạo thành sẽ có số đo bằng nhau. Tính chất này được áp dụng rộng rãi trong việc giải các bài toán về góc trong hình học phẳng.

Tính chất về vị trí tương đối của góc đồng vị

Về vị trí tương đối, góc đồng vị có thể nằm ở hai vị trí khác nhau trên hai đường thẳng song song. Chúng có thể là góc trong – góc trong, góc ngoài – góc ngoài hoặc góc trong – góc ngoài đối.

Khi xét về hướng, hai góc đồng vị luôn có cùng chiều quay. Điều này có nghĩa là nếu một góc quay theo chiều kim đồng hồ thì góc đồng vị với nó cũng sẽ quay theo chiều kim đồng hồ và ngược lại.

Phân biệt góc đồng vị với các loại góc khác trong hình học

Trong hình học, góc đồng vị là góc như thế nào có thể được xác định khi hai đường thẳng song song bị cắt bởi một đường thẳng cắt ngang. Các góc nằm cùng một phía so với đường cắt và có vị trí tương ứng nhau được gọi là góc đồng vị.

Để phân biệt rõ góc đồng vị với các loại góc khác, cần xem xét đặc điểm và tính chất riêng của từng loại. Việc hiểu rõ sự khác biệt giữa các loại góc sẽ giúp đồng quy là gì và các khái niệm hình học khác trở nên dễ dàng hơn.

So sánh góc đồng vị và góc so le trong

Góc so le trong là gì và điểm khác biệt với góc đồng vị có thể thấy rõ qua vị trí của chúng. Góc so le trong nằm ở hai phía khác nhau của đường cắt và nằm trong khu vực giữa hai đường thẳng song song. Ngược lại, góc đồng vị nằm cùng phía đường cắt.

Về số đo, cả góc đồng vị và góc so le trong đều bằng nhau khi hai đường thẳng song song. Tuy nhiên, cách xác định và ứng dụng của chúng trong các bài toán hình học có sự khác biệt đáng kể.

So sánh góc đồng vị và góc kề bù

Góc kề bù và góc đồng vị có mối quan hệ về vị trí hoàn toàn khác nhau. Góc kề bù là hai góc liền kề nhau và có tổng số đo bằng 180 độ. Trong khi đó, góc đồng vị không nhất thiết phải liền kề và có thể nằm ở các vị trí khác nhau trên hai đường thẳng song song.

Việc phân biệt hai loại góc này rất quan trọng trong việc giải các bài toán chứng minh góc. Góc kề bù thường được sử dụng để tìm số đo góc còn thiếu, trong khi góc đồng vị giúp chứng minh sự bằng nhau của các góc.

So sánh góc đồng vị và góc đối đỉnh

Góc đối đỉnh được tạo thành khi hai đường thẳng cắt nhau tại một điểm, tạo ra hai cặp góc đối diện qua đỉnh. Đặc điểm này hoàn toàn khác với góc đồng vị vốn được tạo ra bởi đường cắt và hai đường thẳng song song.

Mặc dù cả góc đối đỉnh và góc đồng vị đều có tính chất bằng nhau trong từng cặp, nhưng cơ sở hình thành của chúng là khác nhau. Góc đối đỉnh bằng nhau do đặc tính của hai đường thẳng cắt nhau, còn góc đồng vị bằng nhau do tính chất của đường thẳng cắt hai đường song song.

Ứng dụng của góc đồng vị trong giải toán hình học

Ứng dụng góc đồng vị là một công cụ quan trọng giúp giải quyết nhiều bài toán hình học phức tạp. Việc nắm vững các tính chất của góc đồng vị sẽ giúp học sinh tiếp cận và giải quyết các dạng toán một cách hiệu quả. Dạy toán trực tuyến sẽ giúp các em hiểu rõ hơn về cách áp dụng góc đồng vị trong hình học qua các dạng bài tập cụ thể.

Bài toán chứng minh hai góc bằng nhau

Khi chứng minh hai góc bằng nhau, góc đồng vị thường được sử dụng kết hợp với các tính chất của đường thẳng song song và các góc kề bù. Phương pháp này đặc biệt hiệu quả khi xét các góc nằm ở hai vị trí khác nhau trong hình.

Một ví dụ điển hình là khi cần chứng minh hai góc bằng nhau trong hình thang. Bằng cách xác định các cặp góc đồng vị và kết hợp với tính chất song song của đáy thang, ta có thể dễ dàng thiết lập được mối quan hệ bằng nhau giữa các góc.

Bài toán tính góc trong hình học phẳng

Trong các bài toán tính góc, việc nhận diện các góc đồng vị giúp rút ngắn quá trình giải bài toán. Thay vì phải tính toán phức tạp, ta có thể áp dụng trực tiếp tính chất bằng nhau của góc đồng vị.

Khi giải quyết các bài toán liên quan đến tứ giác, tam giác, việc xác định các cặp góc đồng vị sẽ giúp thiết lập các phương trình góc nhanh chóng và chính xác. Điều này đặc biệt hữu ích khi xử lý các bài toán về góc nội tiếp, góc tâm trong đường tròn.

Bài toán về đường thẳng song song cắt nhau

Trong các bài toán về đường thẳng song song cắt nhau, góc đồng vị đóng vai trò then chốt để xác định các quan hệ góc. Khi hai đường thẳng song song bị cắt bởi một đường thẳng cắt, các cặp góc đồng vị tạo thành sẽ bằng nhau.

Việc áp dụng tính chất này giúp giải quyết nhiều bài toán phức tạp về góc trong hình học phẳng. Đặc biệt trong các bài toán liên quan đến hình thang, hình bình hành, việc sử dụng góc đồng vị kết hợp với tính chất song song sẽ tạo ra phương pháp giải ngắn gọn và hiệu quả.

Ngoài ra, khi xét các hình phức tạp có nhiều đường thẳng song song và cắt nhau, việc xác định các cặp góc đồng vị sẽ giúp thiết lập được hệ thống các phương trình góc, từ đó tìm ra lời giải cho bài toán.

Phương pháp giải các dạng bài tập về góc đồng vị

Để giải quyết hiệu quả các bài toán liên quan đến góc đồng vị là gì, cần nắm vững phương pháp và các bước giải có hệ thống. Góc đồng vị xuất hiện khi hai góc có cùng giá trị nhưng khác vị trí trên đường tròn lượng giác.

Việc áp dụng đúng phương pháp sẽ giúp xác định chính xác mối quan hệ giữa các góc và đơn giản hóa quá trình giải toán. Điều quan trọng là phải hiểu rõ bản chất của góc đồng vị và các tính chất đặc trưng.

Các bước nhận diện góc đồng vị trong bài toán

Quá trình nhận diện góc đồng vị cần được thực hiện một cách có phương pháp và logic. Trước tiên, cần xác định các góc có cùng giá trị tuyệt đối trên đường tròn lượng giác.

Tiếp theo, kiểm tra vị trí tương đối của các góc trên đường tròn lượng giác. Nếu hai góc có cùng giá trị nhưng khác góc phần tư, chúng có thể là góc đồng vị.

Cuối cùng, áp dụng các công thức chuyển đổi để xác nhận mối quan hệ đồng vị. Việc nhận diện chính xác sẽ quyết định phương pháp giải phù hợp.

Công thức và quy tắc tính toán với góc đồng vị

Khi thực hiện so sánh góc đồng vị, cần áp dụng các công thức cơ bản sau: α ± 2kπ hoặc π – α (với k là số nguyên). Các công thức này cho phép chuyển đổi giữa các góc đồng vị với nhau.

Quy tắc tính toán đòi hỏi sự chính xác và cẩn thận trong việc xác định dấu. Việc xác định đúng góc phần tư và hướng quay của góc sẽ ảnh hưởng trực tiếp đến kết quả.

Ngoài ra, cần lưu ý đến tính chu kỳ của hàm lượng giác khi làm việc với công thức góc đồng vị. Điều này giúp đơn giản hóa các phép tính và tránh sai sót không đáng có.

Ví dụ minh họa và bài tập mẫu

Xét ví dụ: Tìm các góc đồng vị của góc 30° trong khoảng [-360°, 360°].
Áp dụng công thức: α ± 360° = 30° ± 360°

Ta có các góc đồng vị: -330°, 30°, 390°

Một bài tập khác về chứng minh góc đồng vị:
Chứng minh góc 150° và -210° là đồng vị
Giải: 150° = -210° + 360°
Vậy hai góc này là đồng vị

Việc giải nhiều bài tập đa dạng sẽ giúp nâng cao kỹ năng nhận diện và xử lý các góc đồng vị một cách hiệu quả.

Góc đồng vị là gì? Đây là một khái niệm quan trọng trong hình học mà bất kỳ học sinh nào cũng nên nắm vững. Bài viết đã cung cấp những đặc điểm nhận diện, tính chất của góc đồng vị và so sánh với các loại góc khác. Ứng dụng của nó trong giải toán rất phong phú, giúp học sinh có cái nhìn rõ hơn về hình học phẳng. Hãy tiếp tục khám phá để nâng cao kỹ năng toán học của bạn!