Đường chéo hình bình hành: Tính chất và cách tính chi tiết

Đường chéo hình bình hành là kiến thức cơ bản trong toán học mà học sinh cần nắm được. Dạng toán này nằm trong bài giảng của sách giáo khoa, được sử dụng nhiều ở các bài thi và áp dụng trong cả đời sống thực tiễn. Để nghiên cứu rõ hơn, hocthenao sẽ cung cấp đầy đủ kiến thức về tính chất, phương pháp tính toán và một số dạng toán minh hoạ ở bài viết dưới đây.

Tính chất đường chéo hình bình hành

Hình bình hành là một tứ giác có hai cặp cạnh đối song song và bằng nhau. Tính chất chung của hình bình hành bao gồm:

• Cạnh đối: Hai cặp cạnh đối song song và bằng nhau.
• Góc đối: Hai cặp góc đối bằng nhau.
• Đường chéo: Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
• Tổng các góc: Tổng các góc trong một hình bình hành là 360 độ.

Đây là một dạng hình tứ giác có nhiều tính chất hữu ích và quan trọng trong hình học Euclid, đặc biệt là tính chất đường chéo. Tính chất đường chéo hình bình hành gồm:

• Cắt nhau tại trung điểm cắt nhau tại trung điểm của mỗi đường.
• Chia hình bình hành thành hai tam giác bằng nhau.

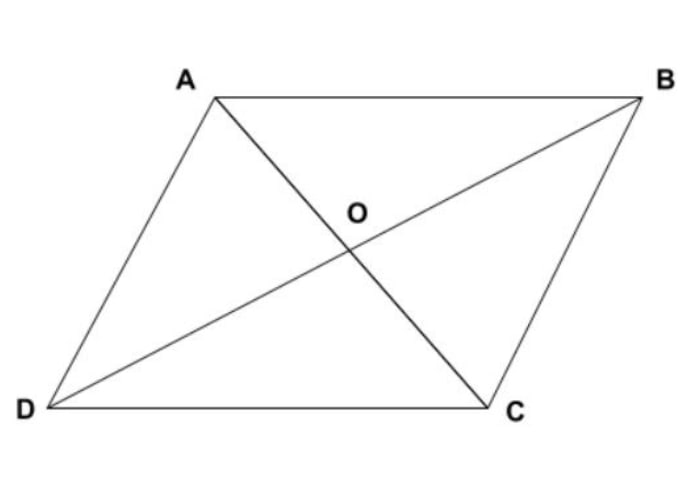
Khám phá bí ẩn hình học: Hình bình hành có tâm đối xứng không?

Phương pháp chứng minh áp dụng tính chất đường chéo hình bình hành

Để chứng minh bằng cách áp dụng tính chất, chúng ta có thể thực hiện theo 2 bước như sau:

1. Chứng minh 2 đường chéo cắt nhau tại trung điểm: Ta có thể chứng minh 1 tứ giác là hình bình hành dựa vào đặc điểm cơ bản (2 đường chéo cắt nhau và chia đôi)
2. Xét các tam giác được tạo bởi 2 đường chéo: Thông qua tính chất cạnh huyền – góc n, chúng ta có thể chứng minh được các tam giác bằng nhau khi 2 đường chéo cắt nhau tại trung điểm.

Dưới đây là ví dụ chứng minh các cạnh song song và bằng nhau, bạn có thể xem lời giải dễ hiểu trong hình ảnh minh họa:

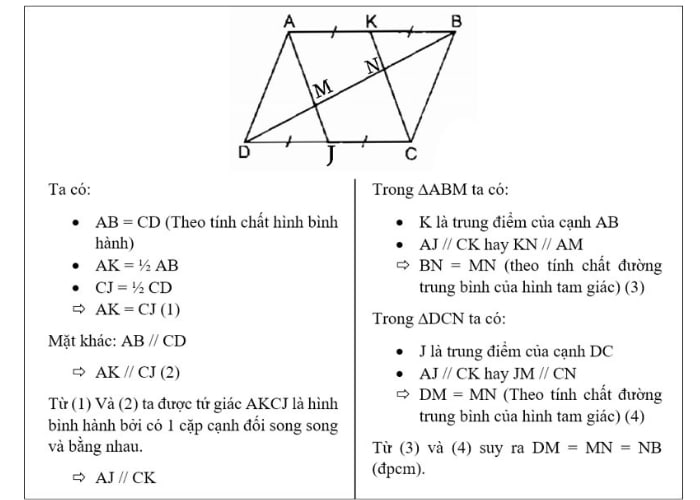
Cách tính đường chéo hình bình hành

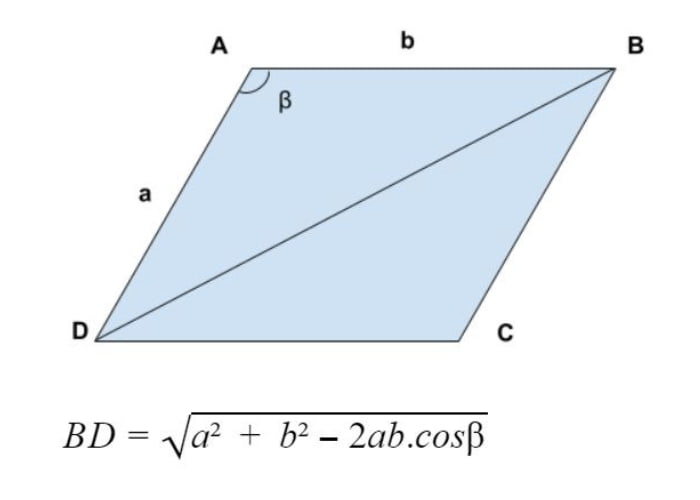
Để tính đường chéo hình bình hành, ta áp dụng công thức sau:

$$d1,2=\sqrt{a^2+b^2-2ab\times\cos\left(\alpha_{1,2}\right)}$$

Trong đó:

• d1, d2 là đường chéo 1 và 2
• a,b là độ dài các cạnh
• $$\alpha_1,\alpha_2\;là\;các\;góc\;được\;tạo\;bởi\;2\;cạnh\;kề\;nhau$$
• $$\alpha_1,\alpha_2\;=180^0$$

Xem thêm: Công thức tính chiều cao hình bình hành, có ví dụ minh họa.

Sau đây là đề bài minh hoạ về cách tính đường chéo hình bình hành: Cho một hbh ABCD có AB= 6cm,BC= 7cm, BD= 8 cm. Hãy tính độ dài AC.

Hướng dẫn giải:

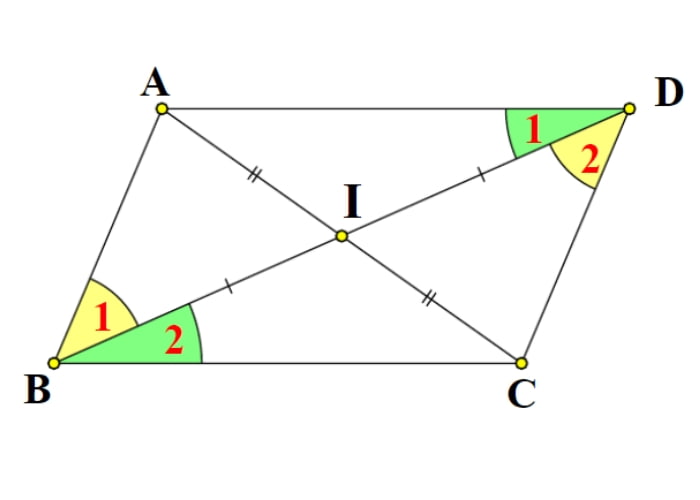
1. Gọi I là điểm giao của hai đường chéo AC và BD: I là trung điểm của cả AC và BD, do đó AI là đường trung tuyến của tam giác ABD.
2. $$Tính\;độ\;dài\;AI:\;Sử\;dụng\;công\;thức\;đường\;trung\;tuyến\;trong\;tam\;giác:\;AI^2=\frac{AB^2+AD^2}2-\frac{BD^2}4$$
3. Tính độ dài AC: Vì III là trung điểm của AC nên: AC= 2AI

Một số dạng toán về đường chéo hình bình hành

Dưới đây là một số dạng toán thường gặp về đường chéo hbh bạn có thể thực hành để củng cố thêm kiến thức:

• Bài Tập 1:Cho hbh PQRS có cạnh PQ = 5 cm và QR = 9 cm. Nếu đường chéo PR = 11 cm, hãy tính độ dài đường chéo còn lại QS sử dụng định lý Pythagoras.
• Bài Tập 2: Trong hình bh WXYZ, biết rằng WX = 10 cm, XY = 14 cm, và đường chéo WZ = 18 cm. Hãy sử dụng công thức tính đường trung tuyến để xác định độ dài XY.
• Bài Tập 3: Chứng minh tứ giác EFGH là hbh có hai đường chéo EF = GH và giao nhau tại trung điểm M của mỗi đường.
• Bài Tập 4: Cho hình bình hành ABCD, biết AB = 6 cm và AC = 10 cm. Tính độ dài của đường chéo BD.
• Bài Tập 5: Cho hbh WXYZ có cạnh WX = 12 cm và đường chéo WZ = 15 cm. Tính độ dài của cạnh XY.
• Bài tập 6: Hbh MNPQ có đường chéo MQ = 20 cm và cạnh MN = 14 cm. Tính độ dài của đường chéo PQ.
• Bài tập 7: Cho hbh EFGH, biết EF = 18 cm và đường chéo EH = 24 cm. Tính độ dài của cạnh FG.
• Bài tập 8: Hình bình hành MNPQ có cạnh MN = 16 cm và cạnh PQ = 20 cm. Biết đường chéo MQ chia tứ giác MNPQ thành hai tam giác đều nhau. Tính độ dài của đường chéo PQ.

Xem ngay: Công thức tính diện tích hình bình hành nhanh chính xác nhất

Ứng dụng của đường chéo hình bình hành trong thực tế

Không chỉ có giá trị trong giảng dạy, mà kiến thức này còn có ứng dụng thực tiễn trong nhiều lĩnh vực khác nhau. Cụ thể:

• Xây dựng và kiến trúc: Được sử dụng để đo đạc và kiểm tra độ chính xác của các phần kết cấu kiến trúc.
• Đo đạc địa lý: Các đoạn đường chéo của hbh được sử dụng để định vị vị trí, tính toán khoảng cách và hướng đi.
• Công nghệ và khoa học: Được sử dụng trong các thiết bị đo lường hiện đại như GPS để xác định vị trí và tính toán khoảng cách.
• Cơ sở toán học: Công thức tính toán đường chéo của hbh (Pythagoras hoặc đường trung tuyến) là cơ sở cho nhiều kiến thức toán học khác.
• Thiết kế đồ hoạ: Ứng dụng trong các phần mềm thiết kế đồ họa để tạo ra các hình ảnh và mô hình số.
• Thương mại và công nghiệp: Nó có thể được áp dụng để tối ưu hóa quy trình sản xuất và lưu thông vật liệu.

Trên đây là những chia sẻ hữu ích về công thức, tính chất và cách tính đường chéo hình bình hành. Hy vọng rằng bài viết sẽ là nguồn kiến thức bổ ích cho bạn. Đừng quên theo dõi thêm bài viết khác của Học thế nào mỗi ngày nhé.