Hình bình hành có tâm đối xứng không? Đây là một câu hỏi thú vị và quan trọng trong hình học. Tâm đối xứng đóng vai trò quan trọng trong việc tính toán và thiết kế, từ đó áp dụng vào nhiều lĩnh vực khác nhau như kiến trúc, công nghiệp, giáo dục. Tuy nhiên, không phải hbh nào cũng có tâm đối xứng. Để hiểu rõ hơn về điều này, mời các bạn cùng theo dõi bài viết dưới đây!
Tâm đối xứng là gì?
Tâm đối xứng là điểm mà khi hình được quay quanh đó 180 độ, hình mới thu được sẽ trùng khớp với hình ban đầu. Đây là một khái niệm quan trọng trong toán và hình học, được sử dụng để mô tả tính chất đối xứng của các hình dạng và cấu trúc.
Tùy thuộc vào đối tượng và không gian nghiên cứu, tâm đối xứng có thể là một điểm, một đường thẳng hoặc một mặt phẳng. Trong không gian hai chiều, tâm đối xứng thường là điểm trung tâm mà quanh đó các phần của hình được phản chiếu tạo thành hình ảnh đối xứng.
Ví dụ:
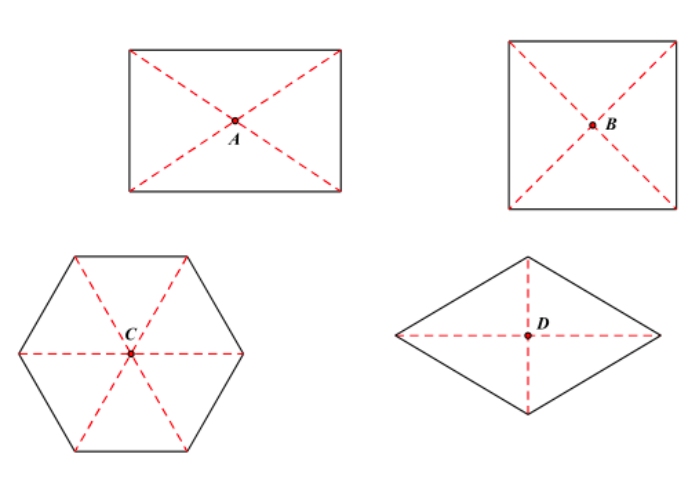
- Hình tròn: Tâm đối xứng tại tâm của nó (vì khi quay quanh điểm này 180 độ, hình tròn vẫn giữ nguyên hình dạng và vị trí).
- Hình vuông, hình thoi, hình bình hành: Tâm đối xứng là giao điểm của hai đường chéo.
Lưu ý:
- Một số hình không có tâm đối xứng, ví dụ như tam giác đều, hình thang cân.
- Có những hình có tâm đối xứng và có nhiều trục đối xứng, ví dụ như hình tròn, hình vuông, hình chữ nhật, hình thoi.
Đọc ngay: Hbh là gì? Công thức tính diện tích, chu vi như thế nào?
Tâm đối xứng của hình bình hành là gì?
Tâm đối xứng của hình bình hành là điểm giao nhau của hai đường chéo của hình. Khi hbh có tâm đối xứng, bạn có thể quay nó 180 độ quanh điểm này và hình vẫn giống như ban đầu.
Tuy nhiên, không phải tất cả các hình bình hành đều có tâm đối xứng.
- Hình chữ nhật và hình thoi là hai loại hbh có tâm đối xứng. Tâm đối xứng của chúng chính là điểm giao nhau của hai đường chéo.
- Hình bình hành thông thường có thể không có tâm đối xứng, vì đường chéo của nó không phải lúc nào cũng cắt nhau tại trung điểm.
Xem ngay: Chiều cao hình bình hành là gì? Có bao nhiêu cách xác định chiều cao hbh?
Hình bình hành có tâm đối xứng không?
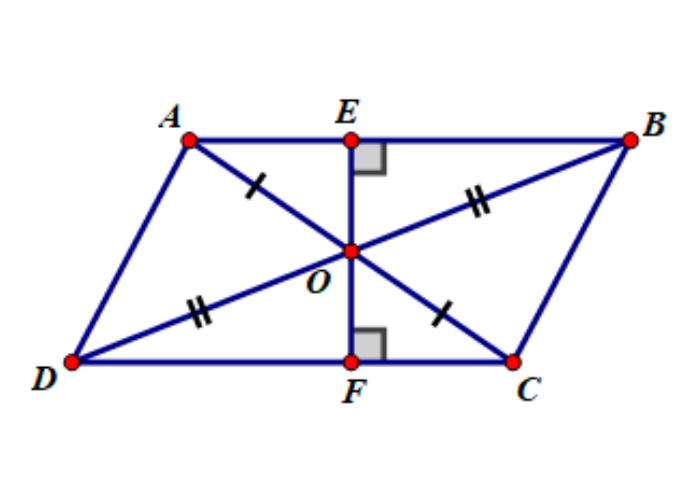
Hình bình hành có tâm đối xứng không? Hình bình hành có tâm đối xứng. Tâm đối xứng của hbh là giao điểm của hai đường chéo. Khi quay hình quanh điểm này 180 độ, hbh sẽ trùng khít với chính nó. Điều này là do hai đường chéo của hbh cắt nhau tại trung điểm của chúng, chia hình thành hai nửa đối xứng nhau.
Tuy nhiên, hình bình hành sẽ không có tâm đối xứng nếu các cạnh của hình không bằng nhau hoặc các góc không phải là 90 độ. Trong trường hợp này, không có điểm nào trên hình mà mỗi điểm đều có một điểm đối xứng tương ứng qua điểm đó.
Tham khảo ngay: Công thức tính diện tích hình bình hành và hướng dẫn giải bài tập minh hoạ đầy đủ, chi tiết nhất
Ứng dụng tâm đối xứng của hình bình hành trong thực tế
Tâm đối xứng của hình bình hành rất quan trọng trong hình học và có nhiều ứng dụng thực tế.
- Tính toán hình học: Khi biết tâm đối xứng, chúng ta dễ dàng tính được diện tích, chu vi và các tỉ lệ khác của hình bình hành.
- Thiết kế: Tâm đối xứng giúp tạo ra các hình dạng đối xứng chính xác, rất quan trọng trong kiến trúc và kỹ thuật.
- Công nghiệp: Trong ngành công nghiệp, tâm đối xứng giúp thiết kế các bộ phận máy móc hoạt động cân bằng và hiệu quả.
- Giáo dục: Trong giáo dục, khái niệm về tâm đối xứng hbh giúp học sinh hiểu rõ hơn về tính chất của hình học phức tạp thông qua bài tập và thí nghiệm.
Như vậy, tâm đối xứng không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế hữu ích.

Xem thêm: Cách tính chu vi hình bình hành, bài tập mẫu minh hoạ và hướng dẫn giải chi tiết
Trên đây là giải đáp cho câu hỏi “hình bình hành có tâm đối xứng không?”. Hy vọng với những giải thích trên, bạn đã hiểu rõ hơn về tính chất đối xứng của hình. Đừng quên để lại bình luận bên dưới nếu bạn muốn tìm hiểu thêm chủ đề khác!




