Kiến thức và công thức tính đường chéo hình lập phương trong toán học

Đường chéo hình lập phương là một khái niệm quan trọng trong hình học không gian. Việc hiểu rõ các công thức và ứng dụng của nó giúp học sinh phát triển kỹ năng tính toán và giải quyết bài toán hiệu quả. Khám phá thêm những đặc điểm, công thức và bài toán liên quan sẽ nâng cao kiến thức của bạn trong lĩnh vực này.

Đường chéo hình lập phương là gì và các đặc điểm cơ bản

Đường chéo hình lập phương là đoạn thẳng nối hai đỉnh đối diện không nằm trên cùng một mặt của hình lập phương. Trong một bảng lập phương, có tổng cộng 4 đường chéo không gian đi qua tâm của hình.

Đường chéo hình lập phương có độ dài bằng nhau và đều đi qua tâm của hình lập phương. Độ dài của đường chéo được tính bằng công thức a√3, trong đó a là độ dài cạnh của hình lập phương. Điều này giúp ta dễ dàng xác định kích thước của hình lập phương khi biết độ dài đường chéo.

Các đặc điểm đường chéo hình lập phương thể hiện tính đối xứng hoàn hảo của khối hình học này. Bốn đường chéo không gian đều tạo với các cạnh của hình lập phương những góc bằng nhau. Góc giữa đường chéo và cạnh của hình lập phương là arccos(1/√3), khoảng 54,7 độ.

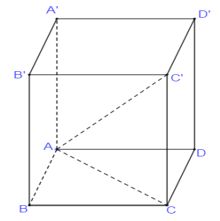
Đường chéo của hình lập phương đóng vai trò quan trọng trong nhiều ứng dụng thực tế, từ thiết kế kiến trúc đến công nghiệp sản xuất. Ví dụ, khi thiết kế khung giàn không gian, các kỹ sư thường sử dụng tính chất của đường chéo để tạo ra cấu trúc vững chắc và cân đối.

Số lượng và phân loại đường chéo trong hình lập phương

Trong hình lập phương, đường chéo được chia thành hai loại chính: đường chéo mặt và đường chéo không gian. Hình lập phương có bao nhiêu đường chéo phụ thuộc vào cách tính tổng của hai loại này. Tổng số đường chéo của một hình lập phương là 24 đường, trong đó có 12 đường chéo mặt và 4 đường chéo không gian. Mỗi loại đường chéo có những đặc điểm và tính chất riêng biệt.

Để hiểu rõ hơn về cấu tạo của hình lập phương, cần nắm được hình lập phương có bao nhiêu cạnh. Từ đó có thể dễ dàng xác định vị trí và số lượng các đường chéo.

Đường chéo mặt của hình lập phương

Đường chéo mặt là đường nối hai đỉnh đối diện trên cùng một mặt của hình lập phương. Mỗi mặt của hình lập phương có hình dạng là hình vuông và có 2 đường chéo. Do hình lập phương có 6 mặt nên tổng số đường chéo mặt là 12 đường.

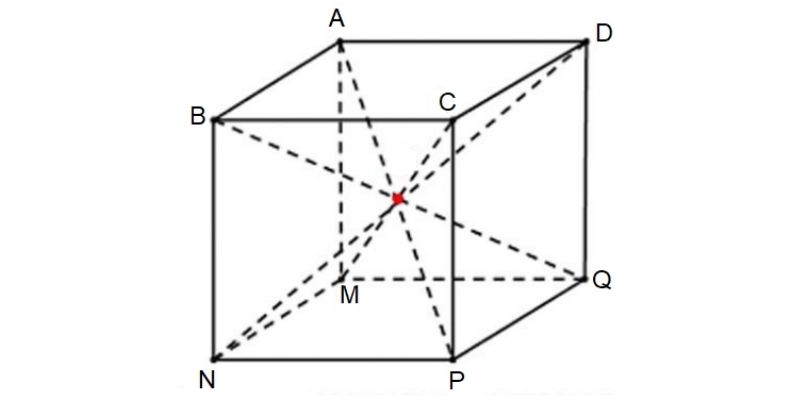
Các đường chéo mặt có độ dài bằng nhau và bằng a√2 (với a là cạnh của hình lập phương). Đường chéo mặt tạo với cạnh của hình lập phương một góc 45 độ. Đây là những yếu tố quan trọng giúp giải các bài toán liên quan đến đường chéo của hình lập phương.

Đường chéo không gian của hình lập phương

Đường chéo không gian là đường nối hai đỉnh đối diện không nằm trên cùng một mặt của hình lập phương. Hình lập phương có tổng cộng 4 đường chéo không gian, các đường này đều đi qua tâm của hình lập phương và có độ dài bằng nhau.

Độ dài của đường chéo không gian được tính theo công thức a√3 (với a là cạnh của hình lập phương). Đường chéo không gian tạo với mặt đáy một góc khoảng 35,26 độ. Các đường chéo không gian đóng vai trò quan trọng trong việc xác định tâm của hình lập phương và tính toán thể tích của các khối đa diện phức tạp.

Công thức tính độ dài đường chéo hình lập phương và cách áp dụng

Công thức tính đường chéo hình lập phương là một trong những kiến thức quan trọng trong toán hình học không gian. Để tính được độ dài đường chéo của hình lập phương, cần phân biệt rõ hai loại đường chéo: đường chéo mặt và đường chéo không gian.

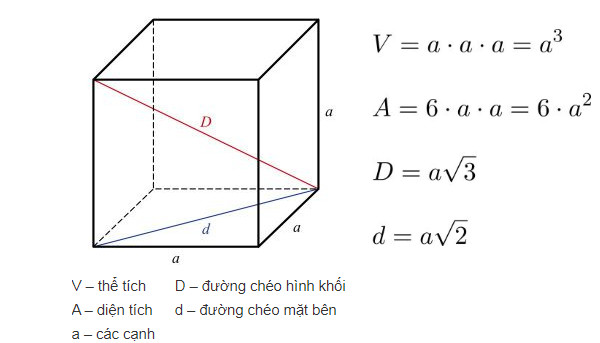
Công thức tính đường chéo mặt

Đường chéo mặt là đoạn thẳng nối hai đỉnh đối diện trên cùng một mặt của hình lập phương. Độ dài đường chéo hình lập phương trên mặt được tính theo công thức: d = a√2, trong đó a là độ dài cạnh của hình lập phương.

Công thức này được xây dựng dựa trên định lý Pytago, khi xét tam giác vuông được tạo bởi đường chéo mặt và hai cạnh kề của hình lập phương. Hai cạnh kề có độ dài bằng nhau và bằng a.

Công thức tính đường chéo không gian

Công thức đường chéo hình lập phương trong không gian là D = a√3, với a là độ dài cạnh của hình lập phương. Đường chéo không gian là đoạn thẳng nối hai đỉnh đối diện không nằm trên cùng một mặt.

Công thức này được thiết lập bằng cách áp dụng định lý Pytago hai lần: một lần cho đường chéo mặt và một lần cho đường chéo không gian. Đường chéo không gian luôn dài hơn đường chéo mặt của cùng một hình lập phương.

Ví dụ minh họa cách tính

Cho hình lập phương có cạnh a = 6cm, tính:

• Đường chéo mặt: d = 6√2 ≈ 8,49cm
• Đường chéo không gian: D = 6√3 ≈ 10,39cm

Khi giải các bài toán về hình lập phương, việc nắm vững hai công thức trên giúp tính toán nhanh chóng và chính xác. Đồng thời cần chú ý đơn vị đo và làm tròn kết quả theo yêu cầu của từng bài toán cụ thể.

Các bài toán thường gặp về đường chéo hình lập phương

Các bài toán đường chéo hình lập phương thường xuất hiện trong chương trình hình học không gian với nhiều dạng khác nhau. Việc nắm vững các công thức và phương pháp tính toán đường chéo hình lập phương giúp học sinh giải quyết hiệu quả các bài tập phức tạp. Dạy toán trực tuyến sẽ giúp bạn làm chủ các dạng bài tập này.

Bài toán tìm độ dài cạnh từ đường chéo

Khi biết độ dài đường chéo của hình lập phương, việc tìm độ dài cạnh trở nên đơn giản thông qua công thức d = a√3, trong đó d là đường chéo và a là cạnh. Để giải bài toán này, ta chỉ cần chia độ dài đường chéo cho căn bậc hai của 3.

Tuy nhiên, một số bài toán yêu cầu tìm cạnh khi biết tỷ số giữa đường chéo và cạnh. Trong trường hợp này, ta cần áp dụng tính chất của tỷ số để thiết lập phương trình và giải quyết.

Bài toán liên quan đến góc giữa đường chéo và cạnh

Góc giữa đường chéo và cạnh của hình lập phương là một yếu tố quan trọng trong nhiều bài toán. Góc này có giá trị không đổi khoảng 54,7 độ, được tính thông qua công thức cos α = 1/√3.

Khi giải các bài toán về góc, việc sử dụng các hệ thức lượng giác trong tam giác vuông là phương pháp chủ đạo. Đặc biệt, các bài toán thường yêu cầu tính toán các yếu tố khác của hình lập phương thông qua góc này.

Bài toán về diện tích tam giác tạo bởi đường chéo

Diện tích tam giác được tạo bởi các đường chéo trong hình lập phương có thể được tính theo nhiều cách khác nhau. Phương pháp phổ biến là sử dụng công thức diện tích tam giác khi biết hai cạnh và góc xen giữa.

Một cách tiếp cận khác là sử dụng tích có hướng của hai vector. Phương pháp này đặc biệt hiệu quả khi bài toán yêu cầu tính diện tích tam giác tạo bởi đường chéo và các cạnh của hình lập phương.

Việc giải quyết các bài toán này đòi hỏi sự kết hợp giữa kiến thức về hình học phẳng và hình học không gian. Nắm vững các công thức cơ bản và phương pháp tiếp cận sẽ giúp việc giải toán trở nên dễ dàng hơn.

Ứng dụng của đường chéo hình lập phương trong thực tế

Ứng dụng đường chéo hình lập phương có vai trò quan trọng trong nhiều lĩnh vực khác nhau. Tương tự như lập phương của một tổng, đường chéo hình lập phương mang tính ứng dụng cao trong thực tiễn. Việc tính toán diện tích đường chéo hình lập phương giúp tối ưu hóa thiết kế và tăng độ chính xác trong thi công các công trình.

Ứng dụng trong xây dựng và kiến trúc

Trong lĩnh vực xây dựng, đường chéo hình lập phương đóng vai trò then chốt khi thiết kế các khối nhà vuông vức. Các kiến trúc sư thường sử dụng phương pháp đo đường chéo để kiểm tra độ vuông góc của công trình, đảm bảo tính đối xứng hoàn hảo.

Tại các công trình cao tầng, việc tính toán đường chéo còn giúp xác định vị trí lắp đặt hệ thống thang máy và các đường ống kỹ thuật. Điều này tương tự như cách đường chéo hình tam giác cân được áp dụng trong thiết kế mái nhà.

Ngoài ra, đường chéo còn được ứng dụng trong việc tính toán lượng vật liệu cần thiết, giúp tối ưu chi phí xây dựng và đảm bảo độ chính xác cao trong quá trình thi công.

Ứng dụng trong thiết kế và công nghiệp

Trong ngành công nghiệp sản xuất, đường chéo hình lập phương được áp dụng rộng rãi trong thiết kế bao bì, container và các sản phẩm có hình dạng khối vuông. Theo nghiên cứu của Viện Thiết kế Công nghiệp, việc tối ưu hóa đường chéo giúp tiết kiệm 15-20% chi phí vận chuyển và lưu trữ.

Các nhà sản xuất thiết bị điện tử cũng sử dụng nguyên lý này trong thiết kế vỏ máy tính, tủ lạnh và các thiết bị gia dụng. Việc tính toán chính xác đường chéo giúp sản phẩm có tính thẩm mỹ cao và độ bền vượt trội.

Trong lĩnh vực robot công nghiệp, đường chéo hình lập phương được ứng dụng để tính toán không gian hoạt động và tối ưu hóa chuyển động của cánh tay robot, nâng cao hiệu quả sản xuất trên dây chuyền tự động.

Kết luận về đường chéo hình lập phương cho thấy đây là một khái niệm toán học quan trọng với nhiều ứng dụng thực tiễn. Việc hiểu rõ các đặc điểm, công thức tính và bài toán liên quan sẽ giúp học sinh nắm vững kiến thức và áp dụng vào cuộc sống. Đường chéo không chỉ là một bài toán lý thuyết, mà còn là cơ sở cho nhiều lĩnh vực như xây dựng, kiến trúc.