Lăng trụ là gì? Định nghĩa, tính chất, công thức và ứng dụng trong toán học

Lăng trụ là gì? Đây là câu hỏi thú vị trong hình học không gian, giúp bạn khám phá khái niệm và tính chất của hình khối này. Hiểu rõ lăng trụ không chỉ cung cấp kiến thức lý thuyết mà còn ứng dụng trong thực tế, làm nền tảng cho các bài toán và công thức tính toán. Cùng nhau tìm hiểu sâu hơn về lăng trụ và những điều thú vị xung quanh nó.

Lăng trụ là gì?

Lăng trụ là gì – một khối hình học ba chiều được tạo thành từ hai mặt đáy song song và các mặt bên là hình chữ nhật. Hai mặt đáy có hình dạng và kích thước giống hệt nhau, có thể là hình tam giác, tứ giác hoặc đa giác. Các mặt bên được tạo ra bằng cách nối các đỉnh tương ứng của hai mặt đáy bằng các đoạn thẳng song song với nhau.

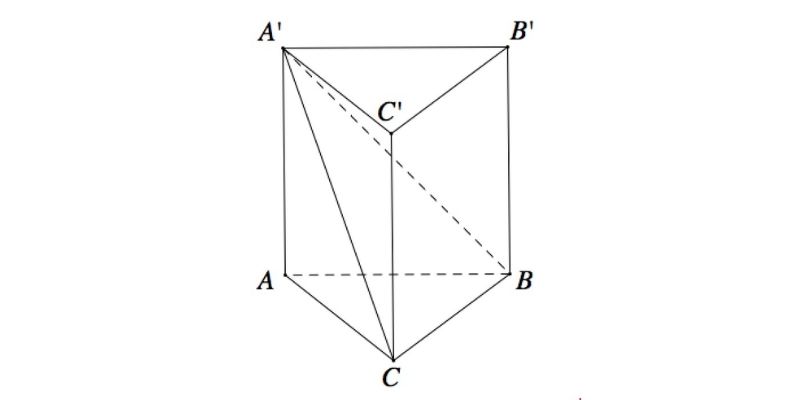
Khi Học toán, việc hiểu rõ định nghĩa lăng trụ giúp học sinh dễ dàng tính toán thể tích và diện tích xung quanh của khối này. Lăng trụ có nhiều ứng dụng trong thực tế, từ thiết kế kiến trúc đến sản xuất công nghiệp. Ví dụ như các tòa nhà cao tầng, hộp đựng đồ, hay các chi tiết máy móc thường có dạng lăng trụ.

Một đặc điểm quan trọng của lăng trụ là chiều cao của nó luôn vuông góc với mặt đáy. Chiều cao này được đo bằng khoảng cách giữa hai mặt phẳng song song chứa hai mặt đáy. Tùy theo hình dạng của mặt đáy, ta có các loại lăng trụ khác nhau như lăng trụ tam giác, lăng trụ tứ giác hay lăng trụ lục giác.

Các đặc điểm nhận dạng và phân loại hình lăng trụ trong không gian

Trong Hình học không gian, lăng trụ là một khối đa diện có những đặc điểm riêng biệt. Việc nắm vững các dấu hiệu nhận biết lăng trụ và cách phân loại giúp chúng ta dễ dàng phân biệt với các khối đa diện khác. Cùng tìm hiểu chi tiết về các đặc điểm và phân loại của hình lăng trụ.

Dấu hiệu nhận biết một hình khối là lăng trụ

Một hình khối được gọi là lăng trụ khi nó có hai mặt đáy song song và bằng nhau. Các mặt bên của lăng trụ là những hình chữ nhật hoặc hình bình hành, được tạo bởi các đường thẳng song song nối các điểm tương ứng của hai đáy.

Khi quan sát một lăng trụ, ta có thể thấy các cạnh bên luôn song song với nhau và vuông góc với mặt phẳng đáy trong trường hợp lăng trụ đứng. Các mặt bên của lăng trụ giao nhau tạo thành các cạnh bên, số lượng cạnh bên bằng số cạnh của đa giác đáy.

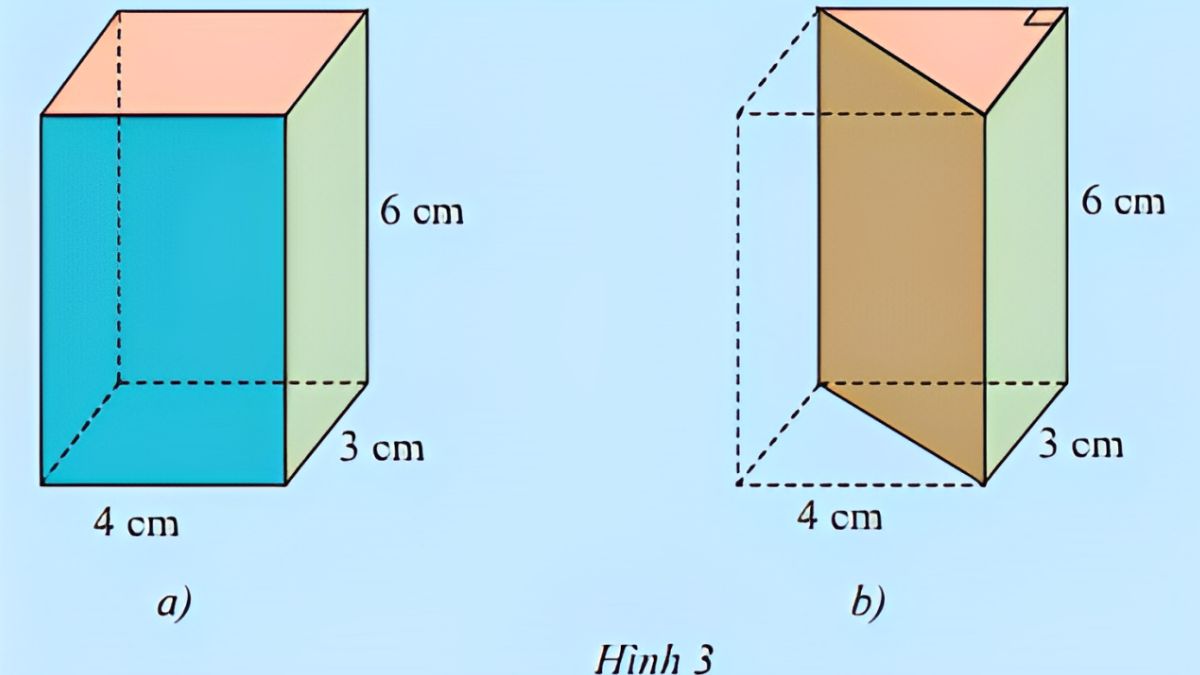
Phân loại lăng trụ theo đáy

Phân loại lăng trụ dựa trên hình dạng của mặt đáy tạo nên nhiều loại lăng trụ khác nhau. Lăng trụ tam giác có đáy là tam giác, thường được sử dụng trong kiến trúc để tạo độ vững chắc cho công trình. Lăng trụ tứ giác với đáy hình chữ nhật hoặc hình vuông phổ biến trong thiết kế nội thất và xây dựng.

Lăng trụ ngũ giác và lục giác thường xuất hiện trong các công trình kiến trúc hiện đại, tạo nên vẻ đẹp độc đáo và ấn tượng. Các loại lăng trụ này mang đến sự đa dạng trong thiết kế và ứng dụng thực tế.

Sự khác biệt giữa lăng trụ đứng và lăng trụ xiên

Lăng trụ đứng và lăng trụ xiên có sự khác biệt cơ bản về cấu trúc hình học. Lăng trụ đứng có các cạnh bên vuông góc với mặt phẳng đáy, tạo nên hình dạng cân đối và ổn định. Các mặt bên của lăng trụ đứng là hình chữ nhật, chiều cao của lăng trụ chính là độ dài cạnh bên.

Ngược lại, lăng trụ xiên có các cạnh bên không vuông góc với mặt phẳng đáy, tạo nên góc nghiêng so với đường vuông góc của mặt đáy. Các mặt bên của lăng trụ xiên là hình bình hành, chiều cao của lăng trụ được tính bằng khoảng cách giữa hai mặt phẳng đáy.

Những tính chất quan trọng của hình lăng trụ

Hình khối lăng trụ là một khối đa diện có hai mặt đáy song song và các mặt bên là hình chữ nhật. Các tính chất của lăng trụ được xác định thông qua mối quan hệ giữa các yếu tố cấu thành như mặt đáy, mặt bên, cạnh bên và chiều cao. Để hiểu rõ hơn về tính chất của lăng trụ, cần phân tích chi tiết từng thành phần cấu tạo nên khối hình học này.

Tính chất về mặt bên và đáy của lăng trụ

Mặt đáy của lăng trụ là hai đa giác đồng dạng và song song với nhau. Chúng có hình dạng và kích thước hoàn toàn giống nhau, chỉ khác vị trí trong không gian. Các mặt bên của lăng trụ là những hình chữ nhật, được tạo thành bởi các cạnh bên nối các đỉnh tương ứng của hai mặt đáy.

Khi khai triển mặt bên của lăng trụ, ta thu được một hình chữ nhật có chiều rộng bằng chu vi đáy và chiều dài bằng chiều cao của lăng trụ. Đây là tính chất quan trọng giúp tính diện tích xung quanh của lăng trụ một cách dễ dàng.

Tính chất về cạnh bên và chiều cao lăng trụ

Các cạnh bên của lăng trụ luôn song song và bằng nhau. Chúng vuông góc với mặt đáy và có độ dài bằng chiều cao của lăng trụ. Lăng trụ là gì có thể được hiểu rõ hơn khi xem xét đặc điểm này – một khối đa diện có các cạnh bên song song và vuông góc với đáy.

Chiều cao của lăng trụ được xác định bằng khoảng cách giữa hai mặt đáy. Đây là đoạn thẳng vuông góc chung với hai mặt đáy, có độ dài không đổi tại mọi điểm. Tính chất này đảm bảo tính đối xứng và ổn định của hình lăng trụ.

Mối quan hệ giữa các yếu tố trong lăng trụ

Các yếu tố trong lăng trụ có mối quan hệ chặt chẽ với nhau. Diện tích toàn phần của lăng trụ bằng tổng diện tích hai mặt đáy và diện tích xung quanh. Thể tích lăng trụ được tính bằng tích của diện tích đáy và chiều cao.

Số mặt của lăng trụ phụ thuộc vào số cạnh của đa giác đáy. Nếu đa giác đáy có n cạnh, lăng trụ sẽ có n+2 mặt (n mặt bên và 2 mặt đáy). Đây là quy luật bất biến giúp xác định nhanh số mặt của bất kỳ lăng trụ nào.

Các công thức tính toán cơ bản về lăng trụ

Để tính toán chính xác các yếu tố của lăng trụ, việc nắm vững các công thức tính lăng trụ là rất quan trọng. Các công thức này giúp xác định diện tích và thể tích của khối hình học này một cách chính xác và hiệu quả.

Công thức tính diện tích xung quanh lăng trụ

Diện tích xung quanh lăng trụ được tính bằng tích của chu vi đáy và chiều cao lăng trụ. Công thức cụ thể là: Sxq = P.h (trong đó P là chu vi đáy, h là chiều cao). Việc áp dụng công thức này giúp tính toán chính xác diện tích phần mặt bên của lăng trụ.

Ví dụ với lăng trụ có chu vi đáy 12cm và chiều cao 5cm, diện tích xung quanh sẽ là: Sxq = 12 x 5 = 60 cm2. Bạn có thể tham khảo thêm về diện tích lăng trụ để hiểu rõ hơn.

Công thức tính diện tích toàn phần lăng trụ

Diện tích toàn phần của lăng trụ bằng tổng diện tích xung quanh và diện tích hai đáy. Công thức là: Stp = Sxq + 2Sd (Sd là diện tích đáy). Khi tính toán cần chú ý đơn vị đo phải thống nhất.

Trong thực tế, việc tính diện tích toàn phần thường áp dụng trong các bài toán thiết kế bao bì, tính lượng vật liệu cần thiết để bọc một khối lăng trụ. Điều này có ý nghĩa quan trọng trong sản xuất và xây dựng.

Công thức tính thể tích lăng trụ

Thể tích lăng trụ được xác định bằng tích của diện tích đáy và chiều cao. Công thức là: V = Sd.h (Sd là diện tích đáy, h là chiều cao). Bạn có thể tìm hiểu chi tiết hơn tại v lăng trụ.

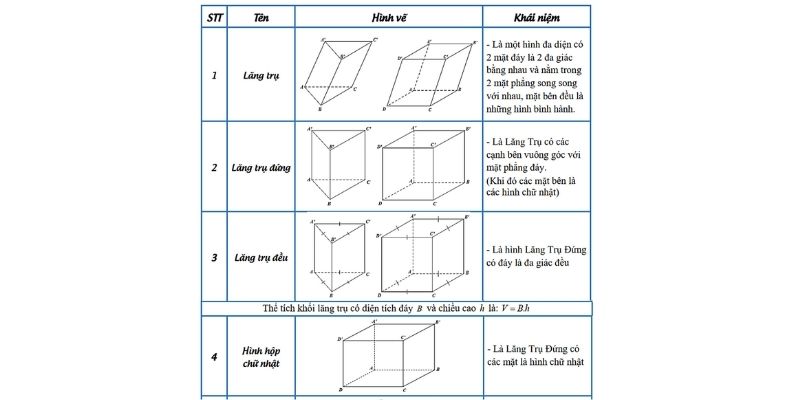
Công thức này áp dụng cho mọi loại lăng trụ, không phụ thuộc vào hình dạng đáy. Điều quan trọng là xác định chính xác diện tích đáy và đảm bảo các phép đo được thực hiện với cùng một đơn vị.

Trong công nghiệp, công thức này thường được sử dụng để tính dung tích các bể chứa, thùng container hay các công trình xây dựng có dạng lăng trụ.

Ứng dụng của lăng trụ trong thực tế và bài toán

Lăng trụ là gì – một khối hình học ba chiều có hai mặt đáy song song và các mặt bên là hình chữ nhật. Hình dạng đặc biệt này tạo nên tính ứng dụng cao trong nhiều lĩnh vực từ kiến trúc đến công nghiệp. Ứng dụng của lăng trụ phổ biến trong thiết kế nhà ở, cầu cống và các công trình xây dựng nhờ tính chất vững chắc, khả năng chịu lực tốt.

Các bài toán thường gặp về lăng trụ

Trong hình học không gian, các bài toán về lăng trụ thường tập trung vào tính diện tích xung quanh, diện tích toàn phần và thể tích. Việc tính toán các yếu tố này đòi hỏi hiểu rõ công thức và mối quan hệ giữa các thành phần của lăng trụ.

Một số bài toán phức tạp yêu cầu tìm góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng trong lăng trụ. Những bài toán này thường xuất hiện trong các kỳ thi và giúp rèn luyện tư duy không gian.

Ứng dụng của lăng trụ trong kiến trúc và đời sống

Trong kiến trúc hiện đại, lăng trụ được ứng dụng rộng rãi để tạo nên những tòa nhà cao tầng ấn tượng. Theo kiến trúc sư Norman Foster, hình dạng lăng trụ giúp tối ưu không gian sử dụng và tăng độ bền vững cho công trình.

Trong đời sống hàng ngày, lăng trụ xuất hiện dưới dạng các vật dụng quen thuộc như hộp đựng, tủ kệ, bàn ghế. Các nhà sản xuất thường chọn thiết kế dạng lăng trụ vì tính tiện dụng và khả năng sắp xếp gọn gàng.

Phương pháp giải các dạng toán về lăng trụ

Để giải các bài toán về lăng trụ, cần nắm vững các bước cơ bản sau:

• Xác định rõ dữ kiện và yêu cầu của bài toán
• Vẽ hình minh họa chính xác, thể hiện đầy đủ các yếu tố cần thiết
• Áp dụng đúng công thức tính toán phù hợp với từng dạng bài

Việc thực hành nhiều bài tập đa dạng sẽ giúp nâng cao khả năng giải quyết các bài toán phức tạp về lăng trụ. Đặc biệt chú ý các trường hợp đặc biệt và biến thể của lăng trụ để có cái nhìn toàn diện về hình học không gian.

Khi tìm hiểu về lăng trụ là gì, bạn sẽ khám phá được nhiều khía cạnh thú vị và hữu ích. Thông qua các đặc điểm, tính chất, công thức tính toán, cũng như ứng dụng thực tế, lăng trụ không chỉ là một hình khối quan trọng trong toán học mà còn góp phần lớn trong kiến trúc và đời sống hàng ngày. Việc nắm rõ những kiến thức này sẽ hỗ trợ hiệu quả trong quá trình học tập và giải quyết bài toán.