Hướng dẫn xác định hai đường thẳng cắt nhau khi nào trong hình học phẳng

Hai đường thẳng cắt nhau khi nào? Đây là câu hỏi quan trọng trong hình học. Để xác định được điều này, bạn cần hiểu rõ về các điều kiện liên quan đến hệ số góc, tọa độ giao điểm và phương trình của hai đường thẳng. Bài viết dưới đây sẽ giúp bạn khám phá những kiến thức cơ bản và ứng dụng thực tiễn trong việc xác định hai đường thẳng cắt nhau.

Hai đường thẳng cắt nhau khi nào?

Hai đường thẳng cắt nhau khi nào là câu hỏi thường gặp trong hình học. Về mặt toán học, hai đường thẳng sẽ cắt nhau khi chúng có một điểm chung duy nhất và không trùng nhau. Điểm chung này được gọi là giao điểm của hai đường thẳng.

Để xác định 2 đường thẳng cắt nhau khi nào, ta cần xét đến phương trình của chúng. Nếu hai đường thẳng có hệ số góc khác nhau, chúng sẽ cắt nhau tại một điểm. Ngược lại, nếu hai đường thẳng có hệ số góc bằng nhau nhưng có tung độ gốc khác nhau, chúng sẽ song song với nhau và không có điểm cắt.

Trong thực tế, việc xác định điểm cắt của hai đường thẳng có ý nghĩa quan trọng trong nhiều lĩnh vực như kiến trúc, xây dựng và thiết kế. Học toán giúp ta hiểu rõ hơn về mối quan hệ giữa các đường thẳng và ứng dụng kiến thức này vào cuộc sống. Ví dụ, khi thiết kế mái nhà, kiến trúc sư cần tính toán chính xác điểm giao nhau của các thanh đỡ để đảm bảo độ vững chắc cho công trình.

Các điều kiện cơ bản để xác định hai đường thẳng cắt nhau trong mặt phẳng

Điều kiện để hai đường thẳng cắt nhau trong mặt phẳng là một vấn đề quan trọng trong hình học phẳng. Để xác định chính xác vị trí giao nhau của hai đường thẳng, cần phải xem xét một số điều kiện cơ bản. Điều kiện hai đường thẳng song song, trùng, cắt nhau là những yếu tố then chốt giúp phân biệt các trường hợp khác nhau.

Điều kiện về hệ số góc của hai đường thẳng

Khi xét hai đường thẳng d1 và d2 có hệ số góc lần lượt là k1 và k2, điều kiện đầu tiên để chúng cắt nhau là k1 ≠ k2. Điều này có nghĩa là hai đường thẳng phải có độ nghiêng khác nhau so với trục hoành.

Nếu hai đường thẳng có phương trình dạng y = k1x + b1 và y = k2x + b2, việc so sánh hệ số góc sẽ cho ta biết ngay khả năng giao nhau của chúng. Khi k1 = k2, hai đường thẳng sẽ song song hoặc trùng nhau.

Điều kiện về tọa độ giao điểm

Để xác định tọa độ giao điểm của hai đường thẳng, ta cần giải hệ phương trình của chúng. Điều kiện để 2 đường thẳng cắt nhau là hệ phương trình này phải có nghiệm duy nhất.

Tọa độ giao điểm phải thỏa mãn đồng thời phương trình của cả hai đường thẳng. Điều này có nghĩa là điểm đó phải nằm trên cả hai đường thẳng và có tọa độ hữu hạn.

Việc tính toán tọa độ giao điểm không chỉ giúp xác định vị trí cụ thể mà còn cho phép kiểm chứng tính hợp lý của kết quả trong không gian tọa độ Descartes.

Điều kiện về phương trình đường thẳng

Khi xét phương trình tổng quát ax + by + c = 0, hai đường thẳng sẽ cắt nhau khi định thức của hệ số không bằng 0. Điều này đảm bảo hệ phương trình có nghiệm duy nhất.

Trong trường hợp phương trình tham số, cần chuyển về dạng tổng quát để kiểm tra điều kiện cắt nhau. Việc biến đổi phương trình giúp đơn giản hóa quá trình xác định mối quan hệ giữa hai đường thẳng.

Ngoài ra, khi làm việc với các dạng phương trình khác nhau, việc thống nhất về một dạng phương trình chuẩn sẽ giúp việc kiểm tra các điều kiện trở nên dễ dàng và chính xác hơn.

Phương pháp xác định giao điểm của hai đường thẳng trong hình học phẳng

Trong Hình học phẳng, việc xác định giao điểm của hai đường thẳng là một bài toán cơ bản và quan trọng. Cách xác định hai đường thẳng cắt nhau có thể được thực hiện thông qua nhiều phương pháp khác nhau, mỗi phương pháp đều có những ưu điểm riêng phù hợp với từng dạng bài toán cụ thể.

Để tìm được giao điểm chính xác, ta cần nắm vững các phương pháp chính và biết vận dụng linh hoạt. Việc lựa chọn phương pháp phù hợp sẽ giúp giải quyết bài toán một cách hiệu quả và nhanh chóng.

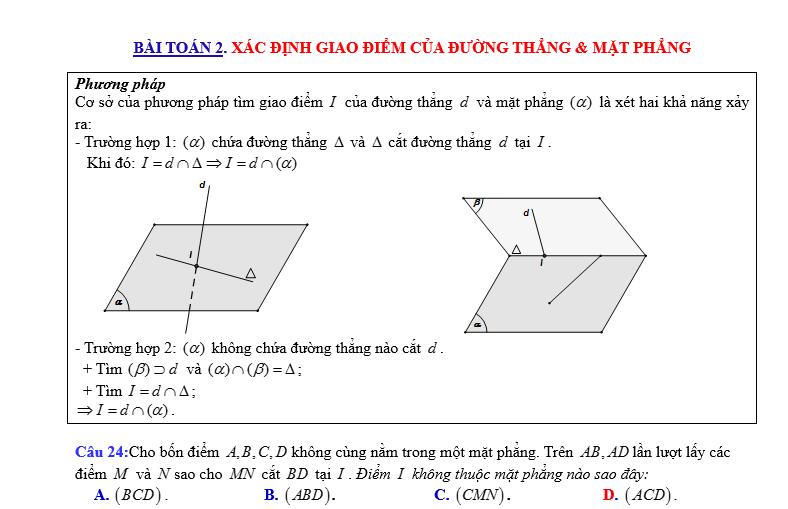
Sử dụng hệ phương trình để tìm tọa độ giao điểm

Phương trình hai đường thẳng cắt nhau có thể được giải quyết bằng cách thiết lập và giải hệ phương trình. Đây là phương pháp phổ biến và chặt chẽ về mặt toán học.

Khi có hai đường thẳng d1: ax + by = c và d2: mx + ny = p, ta chỉ cần giải hệ phương trình này để tìm ra tọa độ giao điểm. Phương pháp này đặc biệt hiệu quả khi các hệ số trong phương trình là những số nguyên hoặc phân số đơn giản.

Trong trường hợp hệ phương trình có nghiệm duy nhất, điểm nghiệm chính là tọa độ giao điểm của hai đường thẳng. Nếu hệ vô nghiệm, hai đường thẳng song song. Còn nếu hệ có vô số nghiệm, hai đường thẳng trùng nhau.

Phương pháp đồ thị để xác định giao điểm

Phương pháp đồ thị là cách tiếp cận trực quan để xác định giao điểm của hai đường thẳng. Bằng cách vẽ chính xác hai đường thẳng trên hệ trục tọa độ, ta có thể xác định được vị trí giao điểm một cách tương đối.

Để áp dụng phương pháp này hiệu quả, cần chú ý đến tỷ lệ và độ chính xác khi vẽ. Việc sử dụng phần mềm đồ họa toán học như GeoGebra có thể giúp tăng độ chính xác và tiết kiệm thời gian.

Phương pháp đồ thị đặc biệt hữu ích trong các bài toán ước lượng hoặc kiểm tra kết quả thu được từ các phương pháp đại số.

Ứng dụng vector trong việc tìm giao điểm

Vector mang lại cách tiếp cận mới mẻ và linh hoạt trong việc tìm giao điểm của hai đường thẳng. Phương pháp này đặc biệt hiệu quả khi hai đường thẳng được cho dưới dạng tham số.

Khi biểu diễn đường thẳng dưới dạng vector, ta có thể sử dụng các phép toán vector để xác định điểm giao. Phương pháp này thường được áp dụng trong các bài toán phức tạp hoặc khi cần tìm thêm các thông tin về góc giữa hai đường thẳng.

Ưu điểm của phương pháp vector là khả năng mở rộng sang không gian ba chiều và tính linh hoạt trong việc chuyển đổi giữa các hệ tọa độ khác nhau.

Đặc điểm và tính chất của hai đường thẳng cắt nhau

Đặc điểm hai đường thẳng cắt nhau thể hiện qua việc chúng giao nhau tại một điểm duy nhất, tạo nên các góc đối đỉnh bằng nhau. Điểm giao này chia mỗi đường thẳng thành hai phần riêng biệt.

Tính chất hai đường thẳng cắt nhau được thể hiện thông qua mối quan hệ hình học giữa các góc và đoạn thẳng tạo thành. Khi hai đường thẳng cắt nhau, chúng tạo ra bốn góc, trong đó các góc đối đỉnh bằng nhau và tổng các góc kề bù bằng 180 độ.

Trường hợp đặc biệt là khi hai vecto vuông góc khi nào, hai đường thẳng sẽ tạo thành bốn góc vuông bằng nhau, mỗi góc 90 độ.

Góc giữa hai đường thẳng cắt nhau

Khi hai đường thẳng cắt nhau, chúng tạo ra bốn góc tại điểm giao. Các góc này có mối quan hệ đặc biệt với nhau theo nguyên lý hình học cơ bản.

Góc giữa hai đường thẳng cắt nhau được xác định bằng góc nhỏ nhất giữa chúng. Nếu gọi α là góc giữa hai đường thẳng, thì góc này luôn nằm trong khoảng từ 0° đến 90°.

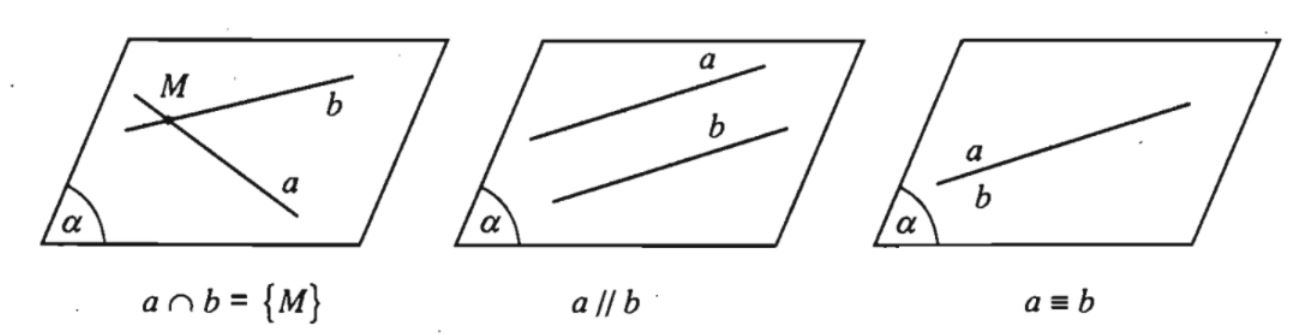
Các góc kề bù tạo thành khi hai đường thẳng cắt nhau có tổng bằng 180°. Điều này là hệ quả trực tiếp từ tính chất của góc phẳng.

Mối quan hệ giữa các đoạn thẳng tạo bởi giao điểm

Giao điểm của hai đường thẳng đóng vai trò như một điểm mốc quan trọng, chia mỗi đường thẳng thành hai tia đối nhau. Các tia này kết hợp với nhau tạo thành các cặp góc đối đỉnh.

Khi hai đường thẳng cắt nhau tại một điểm, chúng tạo ra bốn phần tư mặt phẳng. Mỗi phần tư này được giới hạn bởi hai tia xuất phát từ giao điểm.

Nếu có thêm một đường thẳng thứ ba cắt qua hai đường thẳng ban đầu, các đoạn thẳng được tạo thành sẽ tuân theo định lý về tỷ số của các đoạn thẳng.

Tính chất đặc biệt của hai đường thẳng vuông góc

Hai đường thẳng vuông góc là trường hợp đặc biệt khi góc giữa chúng bằng 90°. Tại điểm giao, bốn góc được tạo thành đều bằng nhau và bằng 90°.

Khi hai đường thẳng vuông góc với nhau, chúng tạo ra một hệ trục tọa độc lập. Hệ trục này thường được sử dụng làm cơ sở cho việc xác định vị trí các điểm trong mặt phẳng.

Tính chất vuông góc còn được ứng dụng rộng rãi trong xây dựng và thiết kế, nơi các kết cấu vuông góc đảm bảo độ vững chắc và tính thẩm mỹ cho công trình.

Ứng dụng của hai đường thẳng cắt nhau trong thực tế và bài toán hình học

Hai đường thẳng cắt nhau xuất hiện phổ biến trong nhiều lĩnh vực của cuộc sống, từ kiến trúc xây dựng đến thiết kế đồ họa. Trong xây dựng, các kỹ sư thường áp dụng nguyên lý này để tạo ra các kết cấu chéo, giúp gia cố độ bền cho công trình.

Trong lĩnh vực thiết kế, ứng dụng hai đường thẳng cắt nhau tạo nên những điểm nhấn thị giác ấn tượng. Theo nghiên cứu của Đại học Stanford, não người có xu hướng tập trung vào các điểm giao nhau, giúp thiết kế trở nên thu hút và dễ nhớ hơn.

Về mặt toán học, hình học hai đường thẳng cắt nhau là nền tảng để giải quyết nhiều bài toán phức tạp liên quan đến góc, khoảng cách và diện tích. Các bài toán này được phân loại thành ba nhóm chính sau đây.

Bài toán về góc

Khi hai đường thẳng cắt nhau, chúng tạo thành bốn góc có những tính chất đặc biệt. Các góc đối đỉnh bằng nhau và tổng các góc kề bù là 180 độ. Đây là cơ sở để giải quyết nhiều bài toán phức tạp hơn.

Trong thực tế, kiến trúc sư Frank Gehry đã áp dụng nguyên lý này khi thiết kế Bảo tàng Guggenheim Bilbao. Các góc cắt nhau tạo nên không gian độc đáo, phá vỡ tính đối xứng truyền thống.

Bài toán về khoảng cách

Khoảng cách giữa hai điểm nằm trên hai đường thẳng cắt nhau có thể được tính toán thông qua định lý Pythagore và các công thức lượng giác. Việc xác định khoảng cách này rất quan trọng trong nhiều ứng dụng thực tiễn.

Trong ngành hàng không, các chuyên gia điều khiển không lưu sử dụng các tính toán tương tự để đảm bảo khoảng cách an toàn giữa các máy bay khi đường bay cắt nhau. Theo quy định của FAA, khoảng cách tối thiểu phải được duy trì là 1000 feet theo chiều dọc.

Bài toán về diện tích

Diện tích các hình tạo bởi hai đường thẳng cắt nhau thường được tính bằng cách chia thành các tam giác hoặc hình thang. Phương pháp này được ứng dụng rộng rãi trong đo đạc địa chính và quy hoạch đô thị.

Một ví dụ điển hình là việc tính toán diện tích các lô đất có hình dạng không đều do đường giao thông cắt qua. Các chuyên gia địa chính sẽ phân chia thành các hình cơ bản để tính toán chính xác diện tích từng phần.

Trong lĩnh vực nông nghiệp, nông dân thường áp dụng phương pháp này để tính diện tích canh tác khi ruộng đồng bị chia cắt bởi các con đường hoặc kênh mương thủy lợi.

Tìm hiểu hai đường thẳng cắt nhau khi nào là rất cần thiết để nắm vững kiến thức hình học. Bài viết đã phân tích các điều kiện cần thiết từ hệ số góc đến tọa độ giao điểm. Ngoài ra, việc xác định giao điểm cũng như các đặc điểm và ứng dụng của hai đường thẳng cắt nhau trong thực tế sẽ giúp bạn củng cố kiến thức hơn nữa. Hãy áp dụng các kiến thức này để giải quyết bài toán một cách hiệu quả!