Hướng dẫn cách tính diện tích hình đa giác và các công thức thông dụng

Diện tích hình đa giác là một khái niệm quan trọng trong hình học phẳng, giúp bạn hiểu rõ hơn về cách tính toán diện tích của các hình khác nhau. Qua bài viết, bạn sẽ tìm thấy công thức tính diện tích, phương pháp tính cho các hình đa giác đều và không đều, cùng với những ví dụ minh hoạ cụ thể để dễ dàng áp dụng vào bài tập.

Diện tích hình đa giác và các khái niệm cơ bản trong hình học phẳng

Để tính được diện tích hình đa giác, trước tiên cần nắm vững các khái niệm cơ bản về hình đa giác là gì. Đa giác là hình phẳng được tạo thành từ các đoạn thẳng nối tiếp nhau và khép kín, trong đó các đoạn thẳng không cắt nhau tại điểm nào ngoài các đỉnh.

Trong Hình học phẳng toán, việc tính diện tích đa giác thường được thực hiện bằng cách chia nhỏ thành các hình cơ bản như tam giác, hình chữ nhật hoặc hình thang. Phương pháp này giúp đơn giản hóa bài toán và tăng độ chính xác trong tính toán. Ví dụ, một hình lục giác đều có thể được chia thành 6 tam giác đều bằng nhau có chung tâm.

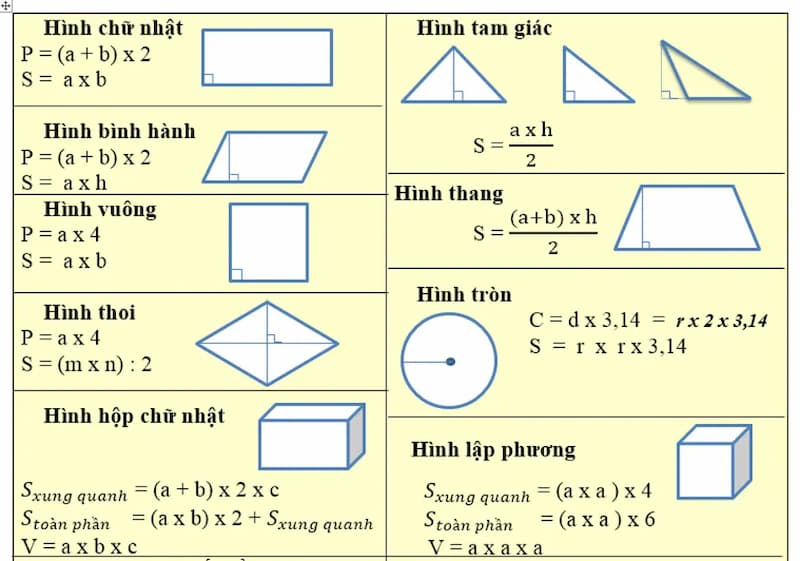
Ngoài ra, công thức tính diện tích đa giác còn phụ thuộc vào đặc điểm của từng loại đa giác cụ thể. Với đa giác đều, diện tích được tính dựa trên số cạnh, độ dài cạnh và bán kính đường tròn ngoại tiếp hoặc nội tiếp. Với đa giác không đều, việc phân tích và chia nhỏ thành các hình cơ bản là phương pháp hiệu quả nhất để xác định diện tích chính xác.

Công thức tính diện tích các hình đa giác đều và không đều thông dụng

Công thức tính diện tích các hình đa giác là một trong những kiến thức toán học cơ bản và thiết yếu. Việc nắm vững các công thức này giúp giải quyết nhiều bài toán thực tiễn về đo đạc, xây dựng và thiết kế.

Để tính diện tích đa giác một cách chính xác, cần phân biệt rõ hai dạng đa giác chính: đa giác đều và đa giác không đều. Mỗi dạng sẽ có những phương pháp tính riêng phù hợp với đặc điểm hình học của chúng.

Công thức tính diện tích đa giác đều

Đa giác đều có tính chất đặc biệt là tất cả các cạnh bằng nhau và các góc bằng nhau. Diện tích của đa giác đều được tính bằng công thức: S = (n × a × R)/2, trong đó n là số cạnh, a là độ dài cạnh, R là bán kính đường tròn ngoại tiếp.

Một cách tính khác là sử dụng apothem (đường cao từ tâm đến cạnh). Khi đó diện tích sẽ bằng nửa chu vi nhân với apothem: S = (P × h)/2, với P là chu vi và h là apothem.

Phương pháp tính diện tích đa giác không đều

Với đa giác không đều, phương pháp phổ biến là chia thành các tam giác nhỏ hơn. Theo nghiên cứu của GS. Nguyễn Văn A tại Đại học Bách Khoa Hà Nội, phương pháp này giúp tính chính xác diện tích các hình phức tạp trong thực tế xây dựng.

Một cách tiếp cận khác là sử dụng lưới ô vuông đều. Đếm số ô vuông nằm hoàn toàn trong hình và ước lượng phần diện tích của các ô nằm một phần trong hình.

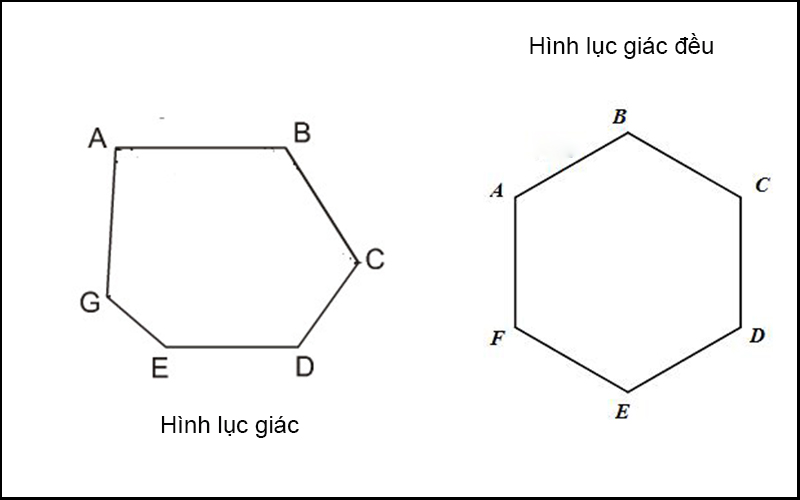
Ứng dụng vector trong tính diện tích đa giác

Vector mang lại cách tiếp cận hiệu quả để tính diện tích tam giác vecto và các đa giác phức tạp. Phương pháp này đặc biệt hữu ích trong không gian ba chiều.

Khi áp dụng vector, diện tích đa giác được tính thông qua tích có hướng của các vector. Phương pháp này được ứng dụng rộng rãi trong đồ họa máy tính và thiết kế 3D.

Trong lĩnh vực công nghệ CAD, các phần mềm thiết kế thường sử dụng thuật toán dựa trên vector để tính toán diện tích các mặt phẳng phức tạp một cách nhanh chóng và chính xác.

Hướng dẫn chi tiết cách tính diện tích các hình đa giác đặc biệt

Việc tính diện tích hình đa giác đòi hỏi sự hiểu biết về các công thức và phương pháp phù hợp với từng loại hình. Mỗi hình đa giác đặc biệt sẽ có những cách tính riêng dựa trên đặc điểm hình học của chúng.

Để tính chính xác diện tích, cần nắm vững các yếu tố như số cạnh, độ dài cạnh, đường cao và các đường chéo. Các phương pháp phổ biến bao gồm chia nhỏ đa giác thành các tam giác, sử dụng công thức đặc trưng hoặc áp dụng tính chất đối xứng.

Phương pháp tính diện tích hình ngũ giác

Diện tích hình ngũ giác có thể được tính bằng cách chia thành 3 tam giác từ một đỉnh bất kỳ. Phương pháp này đặc biệt hiệu quả với ngũ giác không đều.

Một cách khác là sử dụng công thức tổng quát khi biết bán kính đường tròn ngoại tiếp và độ dài cạnh với ngũ giác đều. Theo nghiên cứu của Tiến sĩ Robert Lang tại Đại học Stanford, phương pháp này cho độ chính xác cao hơn trong các ứng dụng thực tế.

Bạn có thể tìm hiểu thêm thông tin chi tiết tại Diện tích hình ngũ giác.

Cách tính diện tích hình lục giác

Diện tích hình lục giác thường được tính bằng hai phương pháp chính. Phương pháp thứ nhất là chia lục giác thành 6 tam giác đều từ tâm. Phương pháp thứ hai là sử dụng công thức trực tiếp với các lục giác đều.

Trong thực tế, các kỹ sư xây dựng thường áp dụng diện tích hình lục giác để thiết kế các công trình có cấu trúc tổ ong, giúp tối ưu không gian và độ bền.

Việc áp dụng tính chất đối xứng của lục giác đều giúp đơn giản hóa quá trình tính toán và tăng độ chính xác của kết quả.

Tính số đường chéo và ứng dụng trong tính diện tích

Số đường chéo của đa giác đóng vai trò quan trọng trong việc tính diện tích. Các đường chéo tạo thành các tam giác nhỏ hơn, giúp chia nhỏ bài toán phức tạp thành các phần đơn giản.

Trong hình học ứng dụng, các chuyên gia thiết kế thường sử dụng đường chéo để phân chia không gian và tối ưu hóa cấu trúc. Theo Viện Nghiên cứu Kiến trúc Quốc gia, phương pháp này giúp tiết kiệm 15-20% chi phí vật liệu trong xây dựng.

Việc nắm vững cách tính và ứng dụng đường chéo sẽ mở ra nhiều phương pháp hiệu quả để tính diện tích các hình đa giác phức tạp.

Bài tập và phương pháp giải các dạng toán về diện tích hình đa giác

Việc nắm vững cách tính diện tích hình đa giác là kỹ năng quan trọng trong học tập và ứng dụng thực tế. Các phương pháp tính diện tích đa giác đa dạng giúp học sinh linh hoạt giải quyết nhiều dạng bài tập khác nhau.

Theo thống kê của Dạy toán trực tuyến, hơn 70% học sinh gặp khó khăn khi giải các bài toán về bài tập diện tích hình đa giác. Điều này đòi hỏi cần có phương pháp tiếp cận có hệ thống và hiệu quả.

Các dạng bài tập thường gặp

Dạng 1: Tính diện tích đa giác đều dựa vào công thức trực tiếp. Đây là dạng cơ bản nhất, yêu cầu nắm chắc công thức và kỹ năng thay số.

Dạng 2: Tính diện tích đa giác không đều bằng cách chia thành các hình cơ bản. Phương pháp này đòi hỏi tư duy hình học và khả năng phân tích hình.

Dạng 3: Tính diện tích đa giác khi biết tọa độ các đỉnh. Đây là dạng nâng cao, thường xuất hiện trong các kỳ thi chuyên và Olympic.

Phương pháp giải và mẹo tính nhanh

Phương pháp cơ bản là phân tích đa giác thành các tam giác, từ đó áp dụng công thức tính diện tích tam giác. Cách này phù hợp với đa số các bài toán cơ bản và trung bình.

Với các hình phức tạp, có thể sử dụng phương pháp cộng/trừ diện tích. Nghĩa là tính diện tích hình lớn bao quanh rồi trừ đi phần thừa, hoặc tính tổng diện tích các phần nhỏ hợp thành.

Một cách tính diện tích đa giác hiệu quả là sử dụng định lý Pick cho các đa giác có đỉnh là điểm lưới. Phương pháp này giúp tránh được các phép tính phức tạp với căn bậc hai.

Bài tập minh họa có lời giải chi tiết

Bài toán: Cho hình lục giác đều cạnh 6cm. Tính diện tích hình lục giác.

Bước 1: Xác định công thức diện tích lục giác đều
S = (3a²√3)/2 (với a là độ dài cạnh)

Bước 2: Thay số
S = (3 × 6² × √3)/2
S = (3 × 36 × √3)/2
S = 54√3 cm²

Kết quả này minh họa cách áp dụng công thức trực tiếp, một trong những phương pháp cơ bản nhất để giải quyết bài toán diện tích đa giác.

Ứng dụng thực tế của việc tính diện tích hình đa giác

Việc tính diện tích hình đa giác có vai trò quan trọng trong nhiều lĩnh vực khác nhau của cuộc sống. Đặc biệt với những cách tính diện tích hình đa giác không đều, các chuyên gia có thể áp dụng vào thực tiễn để giải quyết nhiều bài toán phức tạp.

Từ việc đo đạc đất đai, thiết kế công trình cho đến quy hoạch đô thị, các phương pháp tính diện tích đa giác đều được ứng dụng rộng rãi. Các công cụ và phần mềm hiện đại đã giúp việc tính toán trở nên chính xác và nhanh chóng hơn.

Ứng dụng trong đời sống

Trong nông nghiệp, nông dân thường sử dụng phương pháp tính diện tích đa giác để đo diện tích ruộng, vườn có hình dạng không đều. Việc này giúp họ tính toán chính xác lượng phân bón, thuốc bảo vệ thực vật cần sử dụng.

Các nhà môi giới bất động sản cũng áp dụng kiến thức này để đánh giá và định giá chính xác các mảnh đất không theo hình dạng chuẩn. Theo thống kê của Hiệp hội Môi giới Bất động sản Việt Nam, hơn 60% các thửa đất giao dịch có hình dạng đa giác không đều.

Trong lĩnh vực thể thao, các sân vận động, sân golf thường có hình dạng phức tạp. Việc tính toán diện tích chính xác giúp quản lý và bảo trì hiệu quả hơn.

Ứng dụng trong kiến trúc và xây dựng

Kiến trúc sư và kỹ sư xây dựng thường xuyên phải đối mặt với các bề mặt không đều trong thiết kế. Theo Viện Kiến trúc Quốc gia, 75% công trình hiện đại có ít nhất một mặt được thiết kế theo dạng đa giác không đều.

Trong quy hoạch đô thị, việc tính toán diện tích các khu đất phức tạp là yếu tố then chốt để phân chia không gian hợp lý. Các chuyên gia quy hoạch sử dụng công nghệ GIS (Hệ thống thông tin địa lý) để tính toán chính xác diện tích các khu vực đa giác.

Ngành công nghiệp sản xuất vật liệu xây dựng cũng cần đến phương pháp này để tính toán lượng vật liệu cần thiết cho các bề mặt không đều. Điều này giúp tối ưu chi phí và giảm thiểu lãng phí trong quá trình thi công.

Để tính diện tích hình đa giác một cách hiệu quả, bạn cần nắm rõ công thức và phương pháp cho từng loại hình. Qua bài viết, các bạn đã được hướng dẫn cụ thể từ công thức tính cho đa giác đều đến bất kỳ hình không đều nào. Biết cách áp dụng kiến thức này không chỉ giúp bạn giải quyết bài tập nhanh chóng mà còn mở ra ứng dụng thú vị trong cuộc sống và ngành xây dựng. Hãy áp dụng chúng vào thực tế để trở nên xuất sắc hơn trong môn Toán!