Hình chữ nhật cơ sở của elip là một khái niệm quan trọng trong hình học, đóng vai trò quan trọng trong việc mô tả và hiểu các tính chất của elip. Trong nghiên cứu toán học và ứng dụng thực tiễn, việc hiểu rõ về hình chữ nhật cơ sở này mang lại nhiều lợi ích. Từ việc vẽ đến tính toán, nó giúp đơn giản hóa quá trình nghiên cứu và áp dụng elip vào các bài toán thực tế. Để hiểu rõ hơn, mời các bạn cùng theo dõi thông tin chi tiết trong bài viết dưới đây!
Định nghĩa về hình chữ nhật cơ sở của elip
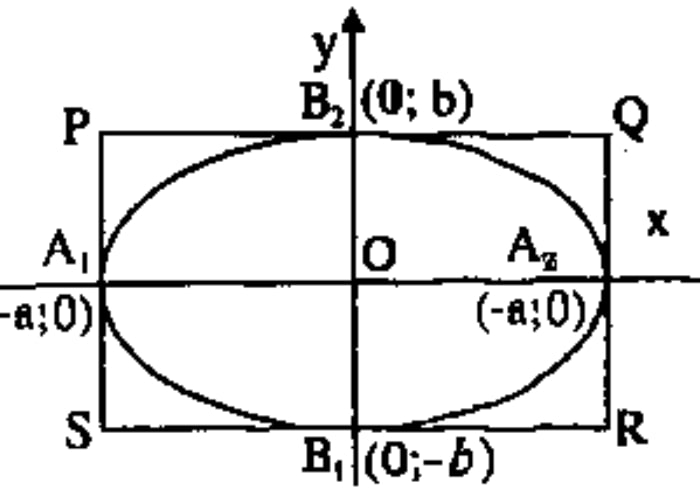
Hình chữ nhật cơ sở của elip là hình chữ nhật đi qua các đỉnh của elip và có các cạnh trùng hoặc song song với các trục tọa độ. Do vậy, tọa độ là (±a, ±b). Nó là một định nghĩa quan trọng trong hình học, nhất là khi nghiên cứu và áp dụng các tính chất của elip.
Phương trình chính tắc của elip:
$$\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1$$
Trong đó:
- h, k: Tọa độ tâm.
- a, b: Lần lượt là nửa độ dài trục lớn và trục nhỏ.
Phương trình đường thẳng:
x = a và y = b
Công thức tính hình chữ nhật cơ sở của elip
3 bước tính toán hình chữ nhật cơ sở cho một elip đã cho như sau:
- Bước 1: Xác định các tham số của elip: Dựa vào phương trình chính tắc của elip: $$\frac{x^2}{a^2}+\frac y{b^2}^2=1$$ Trong đó, a, b là nửa độ dài của trục lớn, trục nhỏ.
- Bước 2: Vẽ HCN cơ sở: Dùng các giá trị của a, b để xác định đường thẳng tạo thành HCN cơ sở: x=a và y=b
- Bước 3: Tính toán diện tích HCN cơ sở: Áp dụng công thức S=4ab, trong đó a, b là độ dài nửa trục của elip.
Tham khảo ngay: Hcn là gì? Khái niệm, tính chất cần biết
Phương trình chính tắc của elip và mối liên hệ với hình chữ nhật cơ sở
Phương trình chính tắc (PTCT) của elip sẽ có dạng:
$$\frac{x^2}{a^2}+\frac y{b^2}^2=1$$
Trong đó, a, b là độ dài bán trục lớn, trục nhỏ của elip.
Hcn cơ sở được định nghĩa bởi các điểm có toạ độ x = a ± c và y = b ± d, thể hiện kích thước tối đa của elip theo hai hướng chính.
Các đặc điểm của HCN cơ sở không chỉ là biểu tượng cho các tính chất hình học của elip một cách rõ ràng, mà còn phản ánh sự đối xứng và kích thước tối đa theo các trục của nó. Mối quan hệ giữa phương trình chính tắc và hình chữ nhật cơ sở cũng đơn giản hóa việc giải quyết các vấn đề trong hình học phẳng liên quan đến elip.
Đọc ngay: Số trục đối xứng của hình chữ nhật là bao nhiêu?
Tính chất của hình chữ nhật cơ sở là gì?
HCN cơ sở của elip đóng vai trò quan trọng trong việc mô tả và hiểu các tính chất của elip. Dưới đây là một số đặc điểm quan trọng của hình chữ nhật cơ sở khi liên kết với elip.
- Định nghĩa: HCN cơ sở được xác định bởi các đường thẳng x = ±a và y = ±b, trong đó a và b là độ dài các bán trục lớn và nhỏ của elip.
- Tính chất đối xứng: Hình chữ nhật cơ sở có tâm đối xứng tại gốc tọa độ, thể hiện tính đối xứng của hình elip mà nó bao quanh.
- Phản ánh kích thước của elip: Với chiều dài 2a và chiều rộng 2b, cho biết kích thước cực đại của elip theo hướng ngang và dọc.
Ngoài ra, hình chữ nhật cơ sở còn là hcn trực giao, có các cạnh song song hoặc vuông góc với trục tọa độ. Điều này làm cho HCN trực giao trở thành công cụ hữu ích trong việc phân tích và tính toán liên quan đến elip.
Đọc thêm: Hình chữ nhật có 2 đường chéo vuông góc là gì?
Ví dụ minh họa một số dạng bài toán về hình chữ nhật cơ sở của elip
Việc sử dụng HCN cơ sở trong các bài toán toán học không chỉ giúp chúng ta hiểu rõ hơn về các đặc tính hình học của elip mà còn là nền tảng để giải quyết nhiều bài toán toán học phức tạp. Dưới đây là một số ví dụ cụ thể:
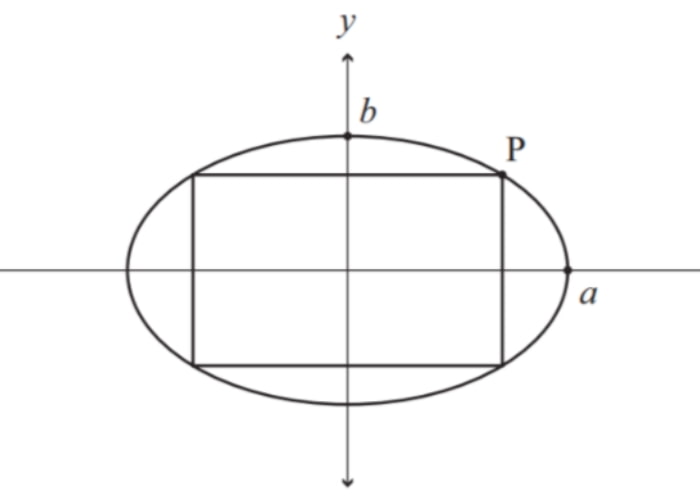
- Xác định các đỉnh: Dựa trên phương trình chính tắc của elip, các đỉnh của hcn cơ sở có thể được xác định tại các điểm (a,b), (a, -b), (-a,-b), (-a,b). Quá trình này giúp bạn dễ dàng vẽ và diễn giải elip trên mặt phẳng tọa độ.
- Tính diện tích: Diện tích của HCN cơ sở được tính bằng công thức S=4ab, trong đó a và b là độ dài của các bán trục của elip. Ví dụ, nếu a=2 và b=3, diện tích sẽ là 4x2x3=24 (đơn vị diện tích).
- Vẽ hình trên mặt phẳng tọa độ: Dựa vào các đỉnh đã xác định và phương trình của các trục, bạn có thể vẽ hcn cơ sở, từ đó trực quan hóa cấu trúc của elip. Quá trình này hỗ trợ trong việc giảng dạy và học tập, giúp làm rõ các đặc tính đối xứng và kích thước của elip.
Xem thêm: Các dấu hiệu nhận biết hcn hay, chi tiết
Ứng dụng hình chữ nhật cơ sở của elip trong thực tế
HCN cơ sở của elip đóng vai trò quan trọng trong đa lĩnh vực, không chỉ trong toán học mà còn trong thực tế, như kiến trúc, thiết kế và khoa học tự nhiên.
- Kiến trúc và xây dựng: Trong kiến trúc, hình elip và hình chữ nhật cơ sở được ứng dụng để tạo ra các cấu trúc như đấu trường, tòa nhà. Các đường cong của elip không chỉ tạo điểm nhấn thẩm mỹ độc đáo mà còn cải thiện tính chịu lực của cấu trúc.
- Thiết kế đô thị: Trong thiết kế đô thị, hình chữ nhật cơ sở giúp tạo ra các không gian công cộng như quảng trường và công viên.
- Khoa học và công nghệ: Trong lĩnh vực khoa học, hình elip được dùng để mô hình hóa quỹ đạo thiên văn và trong công nghệ, hình được áp dụng để thiết kế các bộ phận máy móc hoặc mạch điện tử để hoạt động hiệu quả.
- Thiết kế sản phẩm: Hình elip và hình chữ nhật cơ sở là phần không thể thiếu trong thiết kế sản phẩm, từ đồ gia dụng đến thiết bị điện tử. Loại hình này giúp tối ưu hóa không gian và mang lại tính thẩm mỹ cho sản phẩm.

Như vậy, hình chữ nhật cơ sở của elip là một hình đặc biệt đóng vai trò quan trọng trong việc xác định và nghiên cứu elip. Nắm rõ công thức cũng như cách áp dụng sẽ giúp bạn biết cách giải các bài tập về chủ đề này. Để lại bình luận bên dưới bài viết này nếu bạn còn thắc mắc hay băn khoăn nào khác!
Nội dung bài viết
- 1. Định nghĩa về hình chữ nhật cơ sở của elip
- 2. Công thức tính hình chữ nhật cơ sở của elip
- 3. Phương trình chính tắc của elip và mối liên hệ với hình chữ nhật cơ sở
- 4. Tính chất của hình chữ nhật cơ sở là gì?
- 5. Ví dụ minh họa một số dạng bài toán về hình chữ nhật cơ sở của elip
- 6. Ứng dụng hình chữ nhật cơ sở của elip trong thực tế




