Đường tròn nội tiếp tam giác: Khái niệm, tính chất và công thức tính bán kính

Đường tròn nội tiếp tam giác là khái niệm quan trọng trong hình học, với nhiều ứng dụng thực tiễn. Tâm của đường tròn này được xác định đơn giản bằng giao điểm của ba đường phân giác. Tìm hiểu rõ về đường tròn nội tiếp sẽ giúp bạn nâng cao khả năng giải toán hình học một cách hiệu quả.

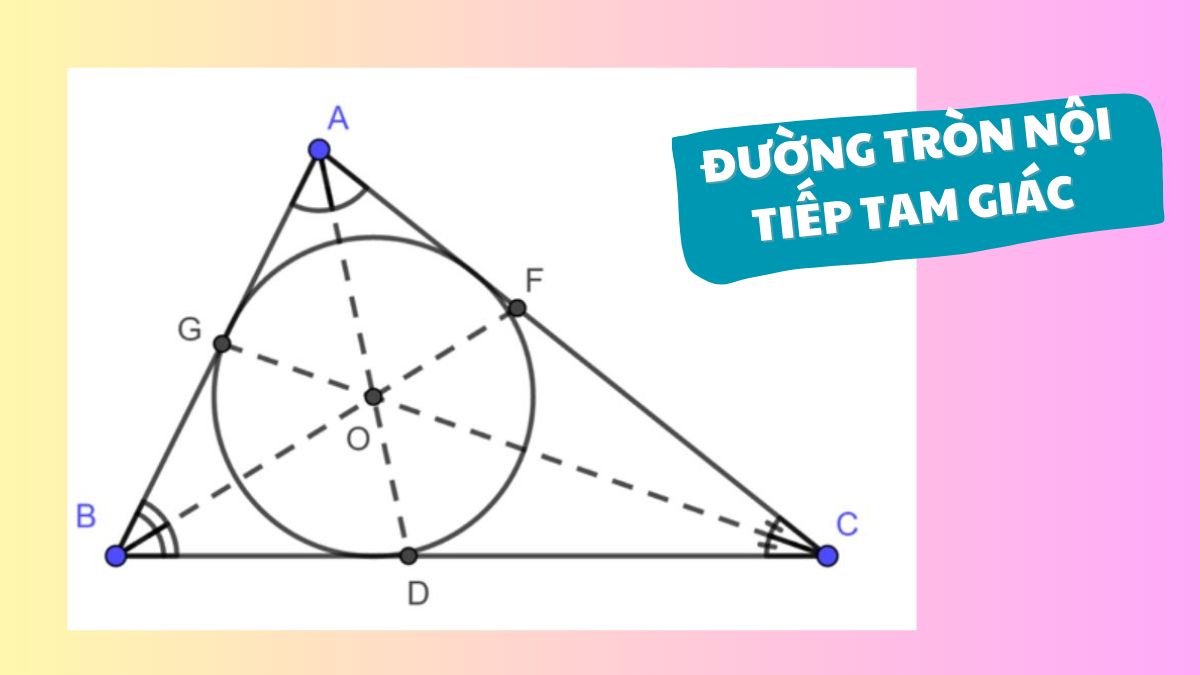
Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả ba cạnh của tam giác

Trong lý thuyết hình học phẳng, đường tròn nội tiếp tam giác là một khái niệm hình học quan trọng. Đây là đường tròn đặc biệt nằm bên trong tam giác và tiếp xúc với cả ba cạnh của tam giác đó tại các điểm tiếp xúc.

Tâm của đường tròn nội tiếp chính là giao điểm của ba đường phân giác của ba góc trong tam giác. Điều này có ý nghĩa quan trọng vì tâm đường tròn nội tiếp luôn cách đều ba cạnh của tam giác. Khoảng cách từ tâm đến mỗi cạnh chính là bán kính của đường tròn nội tiếp.

Một tam giác nội tiếp đường tròn là tam giác có ba cạnh đều tiếp xúc với một đường tròn. Đây là mối quan hệ song phương với đường tròn nội tiếp – nếu một đường tròn nội tiếp một tam giác thì tam giác đó sẽ nội tiếp đường tròn đó. Tính chất này được ứng dụng rộng rãi trong việc giải các bài toán hình học phức tạp.

Bán kính đường tròn nội tiếp có thể tính được thông qua diện tích và chu vi của tam giác. Công thức tính bán kính r = S/p, trong đó S là diện tích tam giác và p là nửa chu vi tam giác. Đây là một trong những công thức cơ bản giúp giải quyết nhiều bài toán liên quan đến đường tròn nội tiếp.

Tâm đường tròn nội tiếp tam giác và cách xác định vị trí

Tâm đường tròn nội tiếp tam giác là điểm đặc biệt nằm bên trong tam giác, có khoảng cách bằng nhau đến ba cạnh của tam giác. Điểm này đóng vai trò quan trọng trong việc xác định vị trí của đường tròn nội tiếp – đường tròn tiếp xúc với cả ba cạnh của tam giác từ bên trong.

Việc xác định vị trí của tâm của đường tròn nội tiếp tam giác có ý nghĩa then chốt trong nhiều bài toán hình học. Điểm này còn được gọi là tâm nội tiếp và thường được ký hiệu là I (Incentre). Từ tâm này, có thể vẽ được đường tròn nội tiếp với bán kính r bằng khoảng cách từ tâm đến mỗi cạnh của tam giác.

Tâm đường tròn nội tiếp là giao điểm của ba đường phân giác

Tâm đường tròn nội tiếp là giao điểm của ba đường phân giác của các góc trong tam giác. Đây là một tính chất quan trọng giúp xác định chính xác vị trí của tâm. Mỗi đường phân giác của một góc trong tam giác là tập hợp các điểm cách đều hai cạnh tạo nên góc đó.

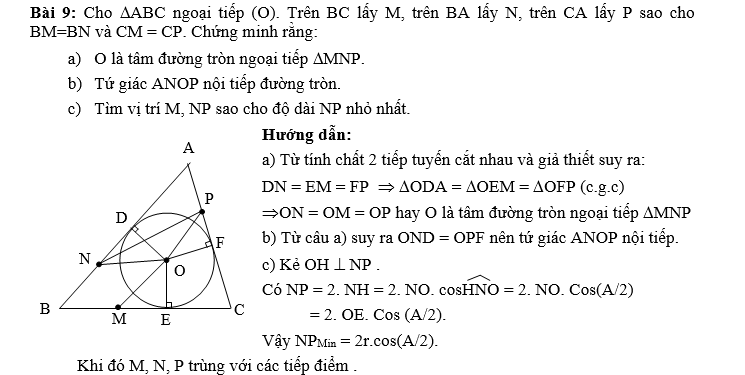
Tâm đường tròn nội tiếp tam giác là gì? Đó chính là điểm giao nhau của ba đường phân giác góc, và điểm này có tính chất đặc biệt là cách đều ba cạnh của tam giác. Tính chất này được chứng minh thông qua định lý về đường phân giác góc và khoảng cách từ một điểm đến đường thẳng.

Phương pháp dựng tâm đường tròn nội tiếp tam giác

Để dựng được tâm đường tròn nội tiếp, cần thực hiện các bước sau một cách chính xác:

• Vẽ đường phân giác của hai góc bất kỳ trong tam giác
• Xác định giao điểm của hai đường phân giác vừa vẽ
• Kiểm tra bằng cách vẽ đường phân giác góc thứ ba, nó sẽ đi qua giao điểm đã tìm được

Tâm đường tròn nội tiếp được xác định chính xác khi ba đường phân giác cắt nhau tại một điểm duy nhất. Điểm này sẽ là tâm của đường tròn nội tiếp cần tìm.

Trường hợp đặc biệt với tam giác đều

Tâm đường tròn nội tiếp tam giác đều trùng với trọng tâm và tâm đường tròn ngoại tiếp của tam giác. Đây là trường hợp đặc biệt do tính chất đối xứng của tam giác đều, nơi ba đường phân giác góc đều tạo với nhau góc 60°.

Trong tam giác đều, khoảng cách từ tâm đến mỗi cạnh đều bằng nhau và bằng r = a(√3 – 1)/3, trong đó a là độ dài cạnh tam giác. Điều này tạo nên một đường tròn nội tiếp hoàn hảo tiếp xúc với cả ba cạnh tại các điểm cách đều nhau.

Công thức tính bán kính đường tròn nội tiếp tam giác và ứng dụng

Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả ba cạnh của tam giác. Việc xác định bán kính đường tròn nội tiếp có ý nghĩa quan trọng trong việc giải các bài toán hình học và ứng dụng thực tiễn.

Công thức tổng quát tính bán kính đường tròn nội tiếp

Bán kính đường tròn nội tiếp tam giác được tính theo công thức r = S/p, trong đó S là diện tích tam giác và p là nửa chu vi tam giác. Công thức này áp dụng cho mọi tam giác, không phụ thuộc vào dạng tam giác.

Một cách khác để tính bán kính đường tròn nội tiếp là sử dụng công thức r = √[(p-a)(p-b)(p-c)/p], với a, b, c là độ dài ba cạnh của tam giác. Công thức này đặc biệt hữu ích khi biết độ dài các cạnh.

Mối liên hệ giữa bán kính và diện tích tam giác

Việc tính bán kính đường tròn nội tiếp tam giác có mối quan hệ mật thiết với diện tích tam giác. Khi biết bán kính đường tròn nội tiếp (r) và bán kính đường tròn ngoại tiếp tam giác, ta có thể xác định được diện tích tam giác thông qua công thức S = pr.

Mối liên hệ này giúp giải quyết nhiều bài toán phức tạp về tam giác, đặc biệt là các bài toán liên quan đến tỷ số diện tích và đường tròn.

Bài tập áp dụng và phương pháp giải

Khi giải các bài toán về đường tròn nội tiếp tam giác, cần xác định rõ các yếu tố đã biết và cần tìm. Thông thường, bài toán sẽ cho biết độ dài các cạnh hoặc diện tích tam giác.

Phương pháp giải thường bao gồm việc tính nửa chu vi p trước, sau đó áp dụng công thức phù hợp. Trong trường hợp bài toán phức tạp, có thể kết hợp với các định lý về tam giác như định lý sin, định lý cosin.

Việc vẽ hình phụ và xác định các yếu tố trung gian cũng rất quan trọng trong quá trình giải bài toán về bán kính đường tròn nội tiếp.

Các tính chất quan trọng của đường tròn nội tiếp tam giác

Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả ba cạnh của tam giác. Tâm của đường tròn nội tiếp chính là giao điểm của ba đường phân giác trong tam giác, còn bán kính được xác định bằng công thức r = S/p (với S là diện tích và p là nửa chu vi tam giác).

Một tính chất đặc biệt của đường tròn nội tiếp là khoảng cách từ tâm đến mỗi cạnh tam giác đều bằng nhau và bằng bán kính đường tròn. Điều này tạo nên sự cân đối và đối xứng trong cấu trúc hình học của tam giác.

Ngoài ra, đường tròn nội tiếp còn có mối liên hệ chặt chẽ với tứ giác nội tiếp là gì khi ta xét các trường hợp đặc biệt của tứ giác được tạo thành từ tam giác ban đầu và các điểm tiếp xúc.

Mối quan hệ giữa đường tròn nội tiếp và tam giác

Đường tròn nội tiếp và tam giác có mối quan hệ hữu cơ thông qua các yếu tố đặc trưng. Tâm đường tròn nội tiếp là giao điểm của ba đường phân giác, điều này chứng tỏ vị trí đặc biệt của nó trong tam giác.

Khi xét về diện tích, tồn tại một công thức liên hệ giữa bán kính đường tròn nội tiếp (r), diện tích tam giác (S) và chu vi tam giác (2p): S = rp. Công thức này thể hiện mối liên hệ chặt chẽ giữa các yếu tố hình học của tam giác và đường tròn nội tiếp.

Các điểm tiếp xúc của đường tròn nội tiếp với các cạnh tam giác cũng tạo thành các đoạn thẳng có tính chất đặc biệt. Chúng chia các cạnh tam giác thành các phần có tỷ số nhất định, góp phần tạo nên cấu trúc hình học độc đáo.

Ứng dụng trong giải toán hình học phẳng

Trong giải toán hình học phẳng, các tính chất của đường tròn nội tiếp thường được áp dụng để giải quyết nhiều bài toán phức tạp. Việc sử dụng công thức tính bán kính đường tròn nội tiếp giúp tìm ra mối liên hệ giữa các yếu tố trong tam giác.

Một ứng dụng quan trọng là sử dụng tính chất về khoảng cách từ tâm đến các cạnh tam giác để chứng minh đẳng thức và bất đẳng thức hình học. Điều này đặc biệt hữu ích khi giải các bài toán về diện tích và độ dài.

Ngoài ra, việc kết hợp tính chất đường tròn nội tiếp với các định lý về tam giác như định lý sin, định lý cosin tạo ra phương pháp hiệu quả để giải quyết các bài toán tổng hợp về tam giác và đường tròn.

Cuối cùng, đường tròn nội tiếp tam giác là một khái niệm quan trọng trong hình học, giúp chúng ta hiểu rõ hơn về mối quan hệ giữa hình học và đại số. Bài viết đã trình bày rõ ràng các đặc điểm như vị trí của tâm đường tròn, công thức tính bán kính và ứng dụng của nó trong thực tiễn. Những kiến thức này không chỉ cung cấp nền tảng vững chắc cho học sinh mà còn hỗ trợ giáo viên và phụ huynh trong việc giảng dạy và hướng dẫn.