Hình lập phương là gì? Định nghĩa, đặc điểm và ứng dụng

Hình lập phương là gì? Hình lập phương là một khái niệm quen thuộc trong toán học và được sử dụng rộng rãi trong cuộc sống hàng ngày. Tìm hiểu cụ thể đặc điểm, ứng dụng và các công thức liên quan của nó.

Hình khối lập phương là gì?

Hình lập phương là một loại khối đa diện có 6 mặt vuông đều, 12 cạnh đều và 8 đỉnh bằng nhau. Các cạnh của hình lập phương giao nhau tại các đỉnh và tạo thành các góc vuông. Bốn đường chéo của hình lập phương cắt nhau tại tâm của hình, tạo thành một hình chữ nhật trong mặt đáy của nó.

Với đặc điểm này, ta có thể suy ra rằng hình lập phương là một hình khối đa diện đều, có tính chất đối xứng và liên quan đến các hình khác như hình vuông, hình bình hành và hình hộp.

Đặc điểm của khối lập phương

Khối lập phương có các đặc điểm sau:

6 mặt vuông đều: Các mặt của hình khối lập phương là các hình vuông có cạnh bằng nhau.
12 cạnh đều: Độ dài của 12 cạnh của hình khối lập phương đều bằng nhau.
8 đỉnh bằng nhau: Các đỉnh của hình khối lập phương đều có cùng khoảng cách với tâm của hình.
4 đường chéo có độ dài bằng nhau: Các đường chéo của hình khối lập phương đều có độ dài bằng nhau, và giao nhau tại tâm của hình.
Tâm của hình lập phương là trung điểm của 4 đường chéo: Điểm giao nhau của 4 đường chéo được gọi là tâm của hình lập phương, và là trung điểm của mỗi đường chéo.

hình lập phương là gì — **Hình hộp lập phương là gì**? Hình lập phương có đặc điểm gì?

Hình lập phương thuộc loại hình khối đa diện đều, cùng với tứ diện đều, khối tám mặt đều, khối mười hai mặt đều, etc. Điểm chung của các hình này là có các mặt đều và các cạnh đều có độ dài bằng nhau.

Các loại hình khối này có tính chất đối xứng và được sử dụng để làm cơ sở cho việc xây dựng các công trình kiến trúc, tạo ra các đồ vật và trong các bài toán toán học phức tạp.

Hình lập phương đáy là hình gì?

Hình lập phương có hình dạng đáy là một hình vuông. Trong không gian hai chiều, hình vuông được coi là một loại hình đặc biệt vì có thể xoay quanh trục của nó mà không thay đổi hình dạng. Do đó, ta có thể hiểu rằng hình lập phương cũng có tính chất này, và có thể xoay quanh trục của nó mà không làm thay đổi kích thước hay hình dạng.

Phân biệt hình lập phương và hình hộp chữ nhật

Cùng có 6 mặt và 12 cạnh, nhưng đâu là điểm khác biệt giữa hình lập phương và hình hộp chữ nhật?

Đặc điểm	Hình lập phương	Hình hộp chữ nhật
Mặt	6 mặt đều là hình vuông	6 mặt, gồm 2 mặt đáy là hình chữ nhật và 4 mặt bên là hình chữ nhật hoặc hình vuông
Cạnh	12 cạnh bằng nhau	12 cạnh, trong đó có 4 cạnh bằng nhau (cạnh đáy) và 4 hoặc 8 cạnh bằng nhau (cạnh bên)
Đỉnh	8 đỉnh	8 đỉnh
Đường chéo	4 đường chéo cắt nhau tại một điểm	4 đường chéo
Góc	24 góc vuông	24 góc vuông
Tính chất	– Mọi cạnh vuông góc với nhau. – Hai đường chéo vuông góc với nhau.	– Các cạnh đối diện song song với nhau. – Các mặt bên vuông góc với mặt đáy.
Công thức tính	– Diện tích xung quanh: $$Sxq=4a^2$$ – Thể tích: $$V=a^3$$	– Diện tích xung quanh: $$Sxq=(a+b)\times2\times h$$ – Thể tích: $$V=a\times b\times h$$ Với a là chiều dài, b là chiều rộng và h là chiều cao
Ví dụ	Viên gạch, xúc xắc	Hộp giày, tủ sách

Các công thức liên quan tới hình lập phương

Dưới đây là một số công thức quan trọng liên quan đến hình lập phương:

Diện tích bề mặt của hình lập phương

Diện tích bề mặt của một hình lập phương được tính bằng tổng diện tích các mặt phẳng của hình này. Với hình lập phương có cạnh độ dài a, diện tích bề mặt S được tính theo công thức:

$$S=6a^2$$

Thể tích của hình lập phương

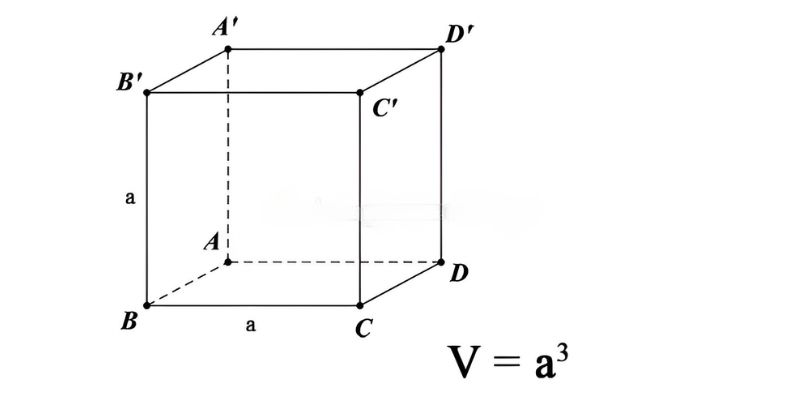
Thể tích của một hình lập phương được tính bằng cách lấy tích của diện tích đáy và chiều cao của hình. Với hình lập phương có cạnh độ dài a, thể tích V được tính theo công thức:

$$V=a^3$$

công thức tính thể tích hình lập phương — Công thức tính thể tích của hình lập phương

Đường chéo của hình lập phương

Đường chéo của một hình lập phương là đoạn thẳng nối hai đỉnh đối diện của hình. Đường chéo của hình lập phương có độ dài bằng cạnh nhân căn bậc hai của 3, tức là:

$$d=a\sqrt3$$

Trong đó:

d là độ dài đường chéo của hình lập phương
a là độ dài cạnh của hình lập phương

Khoảng cách từ tâm hình lập phương đến một đỉnh

Khoảng cách từ tâm của hình lập phương đến một đỉnh của hình bằng nửa độ dài đường chéo của hình, tức là:

$$h=\frac{a\sqrt3}2$$

Trong đó:

h là độ dài khoảng cách từ tâm của hình lập phương tới 1 đỉnh
a là độ dài cạnh của hình lập phương

Ứng dụng của hình lập phương trong cuộc sống

Hình lập phương có nhiều ứng dụng trong cuộc sống hàng ngày, từ những đồ vật đơn giản đến những công trình phức tạp

Rubik

Được ra đời vào năm 1974, Rubik là một trò chơi logic và giải đố được yêu thích trên toàn thế giới. Trong trò chơi này, người chơi cần xoay và di chuyển các khối màu để tạo ra một mặt có màu giống nhau. Với hình dạng hình lập phương và tính chất đối xứng của nó, Rubik là một ví dụ điển hình về ứng dụng của hình lập phương trong cuộc sống.

Con Xúc Xắc

Con xúc xắc là một đồ chơi cổ điển rất quen thuộc với mọi người. Với hình dáng giống hình lập phương, con xúc xắc có tính chất đối xứng và độ dài các cạnh bằng nhau.

Hộp Quà

Hộp quà là một ứng dụng phổ biến khác của hình lập phương trong cuộc sống hàng ngày. Với hình dạng đều, cạnh bằng nhau và tính chất đối xứng, hộp quà hình lập phương không chỉ là nơi chứa quà tặng mà còn là một phần của trải nghiệm mở quà đầy thú vị.

Bài tập vận dụng về hình lập phương

Để hiểu rõ hơn về hình lập phương và áp dụng kiến thức vào thực tế, chúng ta có thể thực hiện một số bài tập sau:

Bài Tập 1: Tính Diện Tích Bề Mặt của Hình Lập Phương

Cho hình lập phương có cạnh a, hãy tính diện tích bề mặt của hình lập phương.

Giải pháp: Diện tích bề mặt của hình lập phương được tính bằng công thức: $$S=6a^2$$. Trong đó, a là độ dài cạnh của hình lập phương.

Bài Tập 2: Tính Thể Tích của Hình Lập Phương

Cho hình lập phương có cạnh a, hãy tính thể tích của hình lập phương.

Giải pháp: Thể tích của hình lập phương được tính bằng công thức: $$V=a^3$$. Trong đó, a là độ dài cạnh của hình lập phương.

Kết Luận

Trong bài viết này, chúng ta đã tìm hiểu về hình lập phương, một loại hình khối đặc biệt trong không gian ba chiều. Nắm rõ khái niệm, đặc điểm, ứng dụng và bài tập vận dụng liên quan đến hình lập phương. Giúp bạn đã có cái nhìn tổng quan và sâu sắc hơn về hình lập phương cũng như cách áp dụng kiến thức này vào thực tế.