Hình tam giác là gì? Đây là một dạng hình học cơ bản và quan trọng trong toán học với nhiều đặc điểm, tính chất riêng biệt. Cùng tìm hiểu các công thức áp dụng đối với loại hình này. Từ đó phân biệt và ứng dụng trong nhiều lĩnh vực khác nhau.
Hình tam giác là gì?
Hình tam giác là một hình học có ba cạnh và ba góc. Hình này được hình thành bởi ba điểm không thẳng hàng gọi là đỉnh. Các đoạn thẳng nối từ đỉnh này đến đỉnh kia gọi là cạnh. Các góc của tam giác được hình thành bởi giao điểm của các cạnh. Tổng 3 góc trong một tam giác luôn luôn bằng 180 độ.
Tam giác được xem là hình đa giác đơn giản trong các dạng hình. Đây cũng là một trong những hình học cơ bản và quan trọng trong chương trình học toán. Bạn sẽ thấy hình tam giác xuất hiện nhiều trong các bài học từ cấp 1 đến cấp 3.
Xem ngay: Cách chứng minh hình tam giác đều trong toán lớp 7
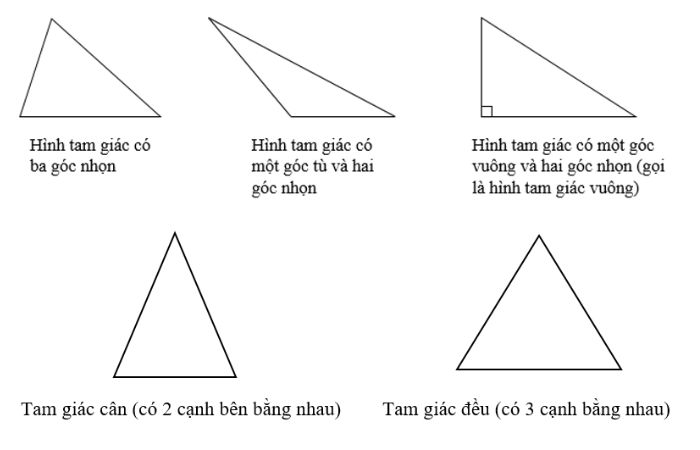
Các loại hình tam giác phổ biến
Bên cạnh khái niệm htg là gì thì việc phân loại cũng cần được nắm vững. Hình tam giác được chia thành nhiều loại khác nhau, dựa trên các đặc điểm riêng biệt. Cụ thể:
- Tam giác đều: Tam giác đều có cả ba cạnh và ba góc bằng nhau. Tất cả các góc của tam giác đều là góc đều (60 độ). Mỗi cạnh của tam giác đều có cùng một độ dài.
- Tam giác vuông: Tam giác vuông có một góc vuông, tức là một góc đo chính xác 90 độ. Cạnh đối diện với góc vuông được gọi là cạnh huyền, trong khi hai cạnh còn lại được gọi là cạnh góc vuông.
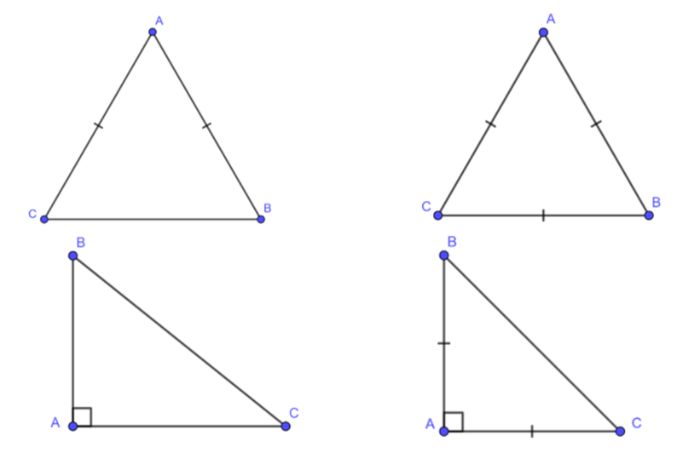
- Tam giác cân: Tam giác cân có ít nhất hai cạnh bằng nhau. Điều này có nghĩa là hai góc ở đỉnh đối diện với các cạnh bằng nhau cũng là góc bằng nhau. Tam giác cân có thể là tam giác cân vuông (có một góc vuông và hai cạnh bằng nhau) hoặc tam giác cân không vuông (có các góc nhọn bằng nhau).
- Tam giác vuông cân: Tam giác vuông cân có cả một góc vuông và hai cạnh bằng nhau. Điều này có nghĩa là tam giác có một góc vuông ở đỉnh và hai cạnh góc nhọn bằng nhau.
- Tam giác nhọn: Tam giác nhọn có ba góc nhọn, tức là cả ba góc đều nhỏ hơn 90 độ.
Tính chất của htg là gì?
Hình tam giác sở hữu nhiều tính chất đặc biệt để ứng dụng trong nhiều lĩnh vực khác nhau. Dưới đây là các tính chất quan trọng nhất mà học sinh cần nắm vững:
- Tổng các góc trong tam giác: Tổng các góc trong tam giác luôn bằng 180 độ. Điều này có nghĩa là tổng các góc A, B và C trong tam giác ABC là 180 độ.
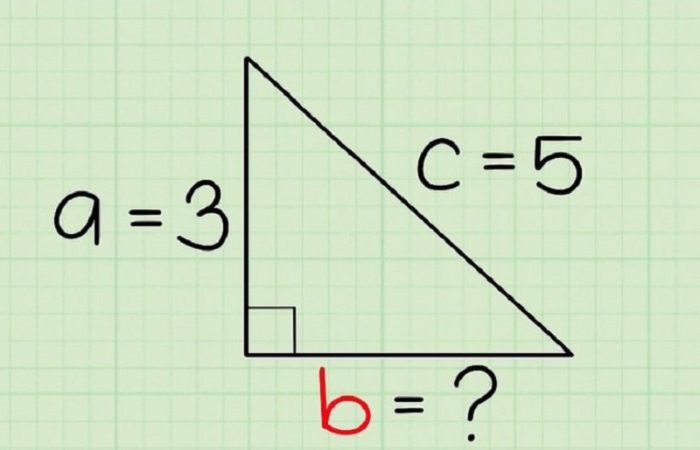
- Định lý Pythagore: Trong tam giác vuông, bình phương của cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh góc nhọn. Định lý Pythagoras có dạng $$a^2+b^2=c^2$$
Trong đó c là cạnh huyền và a, b là hai cạnh góc nhọn.
- Đường cao: Đường cao của tam giác là đoạn thẳng kết nối một đỉnh của tam giác với đường thẳng chứa cạnh đối diện. Đường cao chia tam giác thành các tam giác có diện tích nhỏ hơn.
- Đường trung tuyến: Đường trung tuyến là đường thẳng nối trung điểm của hai cạnh của tam giác. Tam giác có ba đường trung tuyến và chúng giao nhau tại một điểm gọi là trung điểm.
- Đường trung trực: Đường trung trực là đoạn thẳng vuông góc với một cạnh của tam giác và đi qua trung điểm của cạnh đó.
- Đường phân giác: Đường phân giác là đoạn thẳng chia một góc trong tam giác thành hai phần bằng nhau.
Các công thức tính liên quan đến hình tam giác
Dưới đây là các công thức tính liên quan đến hình tam giác:
- Chu vi hình tam giác: Chu vi tam giác bằng tổng độ dài ba cạnh: P = a + b + c, trong đó a, b, c là độ dài ba cạnh của tam giác.
- Diện tích hình tam giác: Sử dụng công thức Heron: $$S\;=\;\sqrt{p(p-a)(p-b)(p-c)}$$.
Trong đó S là diện tích tam giác, a, b, c là độ dài ba cạnh và p là nửa chu vi tam giác.
- Đường cao của tam giác: Đường cao của tam giác tính từ một đỉnh đến đường thẳng chứa cạnh đối diện. Đường cao có thể được tính bằng công thức: $$h\;=\frac{\;2\;\times\;\sqrt{p(p-a)(p-b)(p-c)}}{\;a}$$
Trong đó h là đường cao, a, b,c là độ dài cạnh, p là nửa chu vi của tam giác.
- Đường trung điểm của tam giác: Đường trung điểm của tam giác là đoạn thẳng nối trung điểm của hai đỉnh với đỉnh còn lại. Độ dài đường trung điểm bằng một nửa độ dài cạnh tương ứng.
- Bán kính đường tròn ngoại tiếp: Bán kính đường tròn ngoại tiếp tam giác có thể được tính bằng công thức: $$R\;=\frac{(a\;\times\;b\;\times\;c)}{(4\;\times\;S)}$$
Trong đó a, b, c là độ dài ba cạnh của tam giác và S là diện tích của tam giác.
- Bán kính đường tròn nội tiếp: Bán kính đường tròn nội tiếp tam giác có thể được tính bằng công thức: $$R\;=\frac S{\;p}$$
Trong đó S là diện tích của tam giác và p là nửa chu vi tam giác.
Tìm hiểu thêm: Hướng dẫn chứng minh hình tam giác vuông chi tiết
Một số định lý về hình tam giác
Hình tam giác là đối tượng nghiên cứu của nhiều định lý quan trọng. Các định lý này vừa giúp học sinh giải bài tập, vừa ứng dụng trong các lĩnh vực khác:
- Định lý Pythagoras: Trong một tam giác vuông, bình phương của cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh góc nhọn. Công thức: $$a^2+b^2=c^2$$
Trong đó c là cạnh huyền và a, b là hai cạnh góc nhọn.
- Định lý Sin: Trong một tam giác tù, nhọn hoặc vuông, tỉ lệ giữa độ dài một cạnh và sin của góc đối diện với cạnh đó là như nhau cho cả ba cạnh của tam giác.
- Định lý Cosin: Trong một tam giác, bình phương độ dài một cạnh bằng tổng bình phương độ dài hai cạnh còn lại trừ đi gấp đôi tích của độ dài hai cạnh đó và cos của góc giữa chúng.
- Định lý Stewart: Định lý này cho phép tính độ dài của đoạn thẳng AD khi biết độ dài các cạnh tam giác và tỉ lệ phân chia đường cao.
- Định lý Menelaus: Định lý này liên quan đến sự tương quan giữa các đường thẳng chia tam giác.
Một số dạng toán về hình tam giác
Các bài học liên quan đến hình tam giác rất đa dạng, từ cơ bản đến nâng cao. Trong đó bạn cần nắm vững cách giải các bài tập sau:
- Tìm chu vi tam giác: Được cho độ dài các cạnh tam giác, yêu cầu tính chu vi tam giác bằng cách cộng độ dài các cạnh lại với nhau.
- Tìm diện tích hình tam giác: Được cho độ dài các cạnh tam giác hoặc thông tin đủ để tính diện tích (như độ dài hai cạnh và góc giữa chúng). Yêu cầu tính diện tích tam giác bằng sử dụng công thức Heron hoặc công thức khác tương ứng.
- Tìm đường cao của tam giác: Được cho độ dài các cạnh tam giác hoặc thông tin đủ để tính diện tích. Yêu cầu tính độ dài đường cao từ một đỉnh của tam giác xuống đối diện với cạnh.
- Tìm góc trong tam giác: Được cho độ dài các cạnh tam giác hoặc thông tin khác về tam giác, yêu cầu tính đo độ góc của một hoặc nhiều góc trong tam giác.
Hiểu rõ hình tam giác là gì cũng các kiến thức liên quan là rất quan trọng trong học toán. Do vậy, bạn hãy dành thời gian tìm hiểu và giải các dạng bài tập liên quan. Đây cũng là tiền để để phát triển khả năng tư duy logic và khả năng giải quyết vấn đề.




