Hình thang cân là gì? Định nghĩa, tính chất và ứng dụng bài tập

Hình thang cân là gì? Đây là một tứ giác đặc biệt mà học sinh cấp trung học cơ sở sẽ được tiếp cận. Để hiểu rõ hơn về định nghĩa, tính chất, dấu hiệu nhận biết và ứng dụng của hình thang cân thì bạn hãy theo dõi bài viết dưới đây.

Hình thang cân là gì?

Hình thang cân là một tứ giác có 2 đáy song song, đồng thời có hai góc kề một đáy bằng nhau. Ví dụ như hình thang CDEF có đáy lớn, đáy nhỏ lần lượt là CD và EF, suy ra EF // CD và góc E = F.

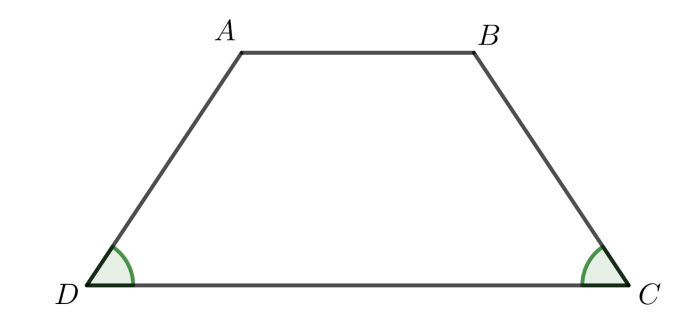
Tính chất hình thang cân

Dưới đây là một số tính chất đặc biệt của hình thang cân mà các bạn học sinh cần ghi nhớ để làm bài tập tốt hơn:

• Hình thang cân có 2 cạnh bên bằng nhau. Ví dụ ABCD là một hình thang cân với 2 đáy lần lượt là AB và CD => AD = BC.
• Hình thang cân có 2 đường chéo bằng nhau. Ví dụ ABCD là một hình thang cân với 2 đáy lần lượt là AB và CD => AC = BD.
• Hình thang cân có 2 góc kề đáy kề nhau. Ví dụ ABCD là một hình thang cân với 2 đáy lần lượt là AB và CD => góc A = góc B và góc C = góc D.
• Hình thang cân có thể nội tiếp một đường tròn, nghĩa là 4 điểm của hình thang đều thuộc 1 hình tròn. Ví dụ hình thang cân ABCD nội tiếp đường tròn tâm O => 4 điểm A, B, C, D cùng thuộc hình tròn tâm O.

Dấu hiệu nhận biết hình thang cân

Hình thang cân là một tứ giác đặc biệt nên có dấu hiệu nhận biết rất rõ ràng. Vậy cách chứng hình thang cân là gì? Bạn có thể dựa vào các dấu hiệu nhận biết hình thang cân dưới đây để nhận hình học này:

• Hình thang có 2 góc kề một đáy bằng nhau là hình thang cân.
• Hình thang có 2 cạnh bên bằng nhau thì có khả năng cao là hình thang cân. Tuy nhiên, nếu sử dụng dấu hiệu này để chứng minh hình thang cân, bạn nên kiểm tra lại 2 đường chéo hay 2 góc kề đáy có bằng nhau không. Nguyên nhân là bởi trên thực tế  vẫn có tứ giác có 2 cạnh bên song song và bằng nhau nhưng không phải hình thang mà là hình bình hành.
• Hình thang nội tiếp một đường tròn là một hình thang cân.

Công thức tính diện tích và chu vi hình thang cân

Công thức tính diện tích hình thang cân: $$S\;=\;(a\;+\;b)\;\times\;h/2$$

Trong đó:

• S: Diện tích hình thang cân
• a và b: Chiều dài của hai cạnh đáy
• h: Chiều cao từ đáy lớn đến đáy bé

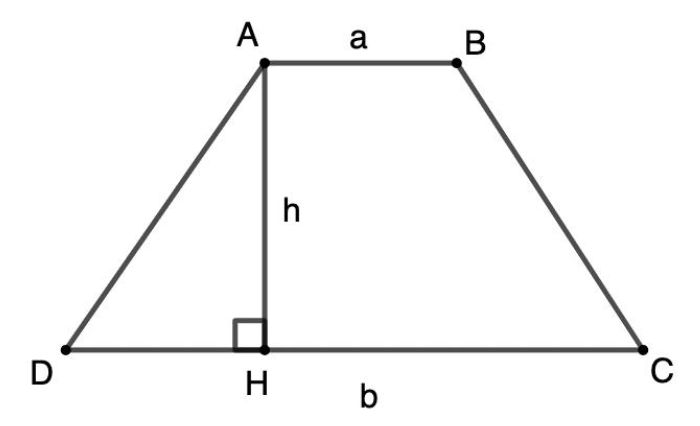
Công thức tính chu vi hình thang cân: $$P\;=\;a\;+\;b\;+\;2c$$

Trong đó:

• P: Chu vi hình thang cân
• a và b: Chiều dài của hai cạnh đáy
• c: Chiều dài của cạnh bên

Cách chứng minh hình thang cân chính xác

Hiện tại có ba cách chứng minh hình thang cân chính. Tùy vào dữ liệu và yêu cầu của bài toán, bạn có thể áp dụng một trong ba phương pháp sau:

Phương pháp 1: Chứng minh hai góc kề một cạnh đáy bằng nhau

Phương pháp:

Bước 1: Xác định các góc kề một cạnh đáy: Nhớ lại rằng trong hình thang, hai góc tạo bởi một cạnh đáy với hai cạnh bên được gọi là hai góc kề một cạnh đáy.

Bước 2: Chứng minh hai góc kề một cạnh đáy bằng nhau: Áp dụng 1 trong 3 cách sau:

• Cách 1: Sử dụng tính chất của đường trung bình trong hình thang: Nếu một đường thẳng đi qua trung điểm của một cạnh bên và song song với hai cạnh đáy, nó cũng sẽ đi qua trung điểm của cạnh bên còn lại. Từ đó suy ra hai góc kề cạnh đáy bằng nhau do đối xứng qua trục đường trung bình.
• Cách 2: Sử dụng định lý Thales: Nếu có thể chứng minh được rằng hai cạnh đối của hình thang song song, thì hai góc kề một đáy sẽ bằng nhau do cùng bù với hai góc ở đáy kia của hình thang.
• Cách 3: Áp dụng các tính chất đường phân giác của tam giác: Nếu có thể chứng minh được rằng đường phân giác của một góc ở đáy đi qua trung điểm của cạnh đối diện, ta suy ra hai góc kề đó bằng nhau, vì đường phân giác tạo thành hai tam giác cân.

Bước 3: Suy ra hình thang cân: Sau khi chứng minh được hai góc kề một cạnh đáy bằng nhau, ta có thể suy ra hình thang đó là hình thang cân dựa vào định nghĩa: Hình thang có hai góc kề một cạnh đáy bằng nhau gọi là hình thang cân.

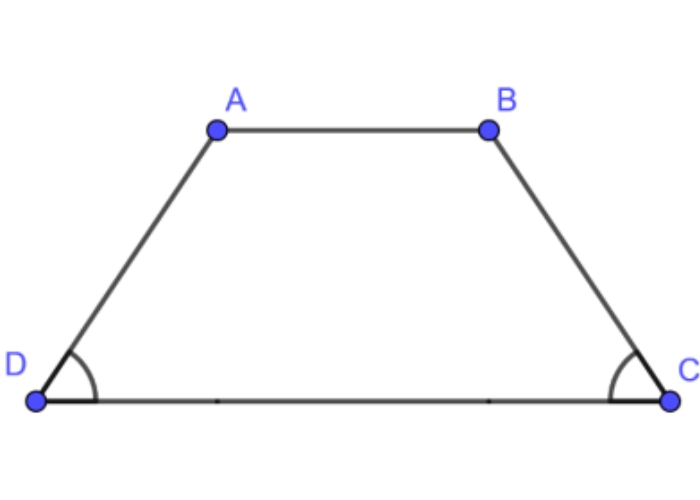
Ví dụ:

Cho hình thang ABCD (AB // CD) có ∠A = ∠C. Chứng minh ABCD là hình thang cân.

Giải

Xác định các góc kề một cạnh đáy:

Góc A và góc C là hai góc kề cạnh đáy CD.

Chứng minh hai góc kề một cạnh đáy bằng nhau:

Ta có ∠A = ∠C (đề bài).

Suy ra hình thang cân:

Theo định nghĩa, hình thang có hai góc kề một cạnh đáy bằng nhau gọi là hình thang cân. Do đó, ABCD là hình thang cân.

Xem ngay: Tổng hợp các dấu hiệu nhận biết hình thang cân đầy đủ, chi tiết nhất

Phương pháp 2: Chứng minh hai đường chéo bằng nhau

Phương pháp: 

Để chứng minh hai đường chéo của hình thang cân bằng nhau, bạn có thể áp dụng phương pháp sử dụng các tam giác đồng dạng bên trong hình thang. Dưới đây là các bước chi tiết:

Bước 1: Xác định và vẽ hình: Vẽ hình thang cân ABCD, trong đó AB, CD là hai đáy, AC, BD là hai đường chéo.

Bước 2: Chứng minh các tam giác đồng dạng:

• Chứng minh tam giác ABD đồng dạng với tam giác CDB bằng cách sử dụng định lý về các góc.
• Vì AB song song với CD, góc ABD bằng góc CDB do hai góc này là góc so le trong.
• Sử dụng tính chất tam giác đồng dạng: Khi tam giác ABD đồng dạng với tam giác CDB, theo tính chất của tam giác đồng dạng, ta có AC/BD = AD/BC.

Bước 3: Áp dụng giả thiết hai đường chéo bằng nhau:

• Do giả thiết BD = AC, suy ra BC = AD.
• Kết luận: Vì AD = BC và các tam giác đồng dạng, hai đường chéo AC, BD bằng nhau, chứng tỏ hình thang là cân.

Ví dụ: 

Cho hình thang ABCD (AB // CD) có hai đường chéo AC và BD bằng nhau. Chứng minh ABCD là hình thang cân.

Giải

Vẽ hình thang ABCD với hai đường chéo AC và BD cắt nhau tại E.

Kẻ đường trung tuyến ME của tam giác ABD.

Ta có ME là đường trung tuyến của tam giác ABD nên: AE = EB.

Xét hai tam giác ABE và CBE:

• AB chung.
• AE = EB (đã chứng minh).
• BE chung.

Vậy tam giác ABE ~ tam giác CBE (c.c.c).

Suy ra: góc BAE = góc CBE (cặp góc tương ứng).

Ta lại có: Góc BAE và góc CBE là hai góc kề một đáy của hình thang ABCD.

Do đó, ∠BAD = ∠BCD (1).

Xét hai tam giác ACD và BCD:

• CD chung.
• AC = BD (đề bài).
• AD = BC (đã chứng minh ở (1)).

Vậy tam giác ACD ~ tam giác BCD (c.c.c).

Suy ra: góc CAD = góc CBD (cặp góc tương ứng).

Ta lại có: Góc CAD và góc CBD là hai góc kề một đáy của hình thang ABCD.

Do đó, ∠ADC = ∠BCD (2).

Từ (1) và (2), suy ra: ∠BAD = ∠ADC, ∠BCD = ∠BCD.

Vậy ABCD là hình thang cân (định nghĩa).

Phương pháp 3: Sử dụng tính chất hình thang nội tiếp đường tròn

Phương pháp:

• Bước 1: Vẽ đường tròn ngoại tiếp: Vẽ đường tròn đi qua tất cả các đỉnh của hình thang.
• Bước 2: Chứng minh các góc bằng nhau: Sử dụng tính chất hai góc nội tiếp cùng chắn một cung để chứng minh các góc kề một đáy hoặc các góc tạo bởi một cạnh đáy và một đường chéo bằng nhau.
• Bước 3: Suy ra hình thang cân: Dựa vào định nghĩa hoặc các dấu hiệu nhận biết hình thang cân để kết luận.

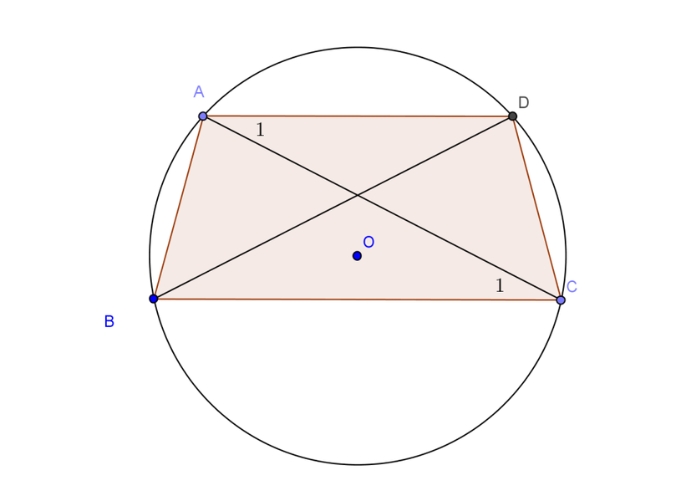
Ví dụ: 

Cho hình thang ABCD (AB // CD) nội tiếp đường tròn (O). Chứng minh ABCD là hình thang cân.

Giải

Vẽ đường tròn (O) đi qua các điểm A, B, C, D.

Ta có:

• ∠BAD và ∠BCD là hai góc nội tiếp cùng chắn cung BD.
• ∠ADC và ∠ABC là hai góc nội tiếp cùng chắn cung AC.

Theo tính chất hai góc nội tiếp cùng chắn một cung:

• ∠BAD = ∠BCD (1)
• ∠ADC = ∠ABC (2)

Xét hai tam giác ABD và CBD:

• AB = CD (do AB // CD).
• ∠BAD = ∠BCD (đã chứng minh ở (1)).

Góc ABD và góc CBD chung.

Vậy tam giác ABD ~ tam giác CBD (g.c.g).

Suy ra: AD = BC (cặp cạnh tương ứng).

Do đó, ABCD là hình thang cân (định nghĩa).

Một số dạng bài tập về hình thang cân thường gặp

Để nắm rõ hơn các kiến thức gồm định nghĩa, tính chất và dấu hiệu nhận biết htc là gì, các bạn học sinh cần luyện nhiều bài tập. Dưới đây là một số dạng bài tập về hình học này thường gặp nhất:

Dạng 1: Tính chu vi hình thang khi biết độ dài các đáy và cạnh bên

Với dạng bài này, mọi yếu tố cần biết để tính chu vi hình thang đã được cho sẵn. Do đó, các bạn học sinh chỉ cần xác định đúng đâu là độ dài của cạnh đáy, cạnh bên và lắp vào công thức là ra. Dưới đây là bài tập ví dụ về dạng bài này:

Bài tập: Cho hình thang ABCD có độ dài hai đáy AB, CD lần lượt là 8cm và 10cm. Cạnh bên AD = BC = 7cm. Tính chu vi của hình thang này.

Lời giải

Theo công thức tính chu vi hình thang cân, ta có chu vi ABCD là: $$P\;=\;8\;+\;10\;+\;(2\;\times\;7)\;=\;32cm$$

Vậy chu vi hình thang cân ABCD là 32cm.

Dạng 2: Tính độ dài cạnh bên của hình thang cân

Với dạng bài này, học sinh cần linh hoạt trong việc sử dụng các công thức, tùy thuộc vào dữ liệu đề bài cho. Dưới đây là các dạng bài tập mà bạn có thể tham khảo:

Bài tập 1: Cho hình thang cân ABCD (AB // CD, AB < CD) với độ dài 2 đáy lần lượt là 4 và 6cm. Chu vi của hình thang là 16cm. Tính cạnh bên AD của hình thang đó.

Lời giải:

Độ dài của cạnh bên AD là: $$AD\;=\;16\;-\;(4+6)/2\;=\;3cm$$

Vậy AD có độ dài bằng 3cm.

Bài tập 2: Cho hình thang cân ABDC (AB // CD, AB < CD), biết độ dài 2 đáy lần lượt là 10 và 16cm. Đường cao AH và BF bằng 18cm. Tính độ dài 2 cạnh bên AC và BD.

Lời giải:

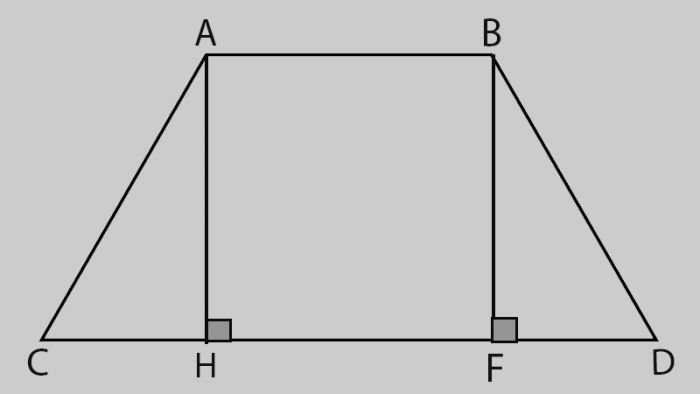
Vì ABCD là hình thang => AC = BD và góc D = góc C

=> tam giác AHC = tam giác BFD (cạnh huyền – góc nhọn)

=> CH = FD

Xét tứ giác ABFH có AH = BF, AH // BF và AH HF

=> ABFH là hình chữ nhật => AB = HF

Ta có HC + HF + FD = 16cm

=> HC = FD = 3cm

Có AC = CH2 + AH2 = 37 cm (định lý pitago)

Vậy AC = BD = 37 cm

Dạng 3: Tính diện tích hình thang cân

Dưới đây là bài tập ví dụ tính diện tích hình thang cân mà bạn có thể tham khảo:

Đề bài: Cho hình thang cân ABCD có độ dài hai đáy AB, CD lần lượt là 8cm và 10cm, đường cao AH bằng 12cm. Tính diện tích hình thang đó.

Lời giải:

Diện tích hình thang cân ABCD là: $$S\;=\;(8\;+\;10)\;\times\;122\;=\;108\;cm^2$$

Vậy diện tích hình thang cân ABCD bằng 108cm2

Ứng dụng của hình thang cân trong thực tế

Ngoài việc hiểu hình thang cân là gì trong toán học, các em học sinh cũng cần phải biết ứng dụng của hình học này trong thực tế. Các tính chất, công thức tính hình thang cân được sử dụng trong nhiều lĩnh vực khác nhau. Cụ thể như sau:

• Thiết kế: Các tính chất, công thức tính chu vi thường được áp dụng để tính toán kích thước khi thiết kế các đồ vật có dạng hình thang cân như túi xách, kệ sách,…
• Công nghiệp: Có nhiều linh kiện của máy móc được sản xuất theo dạng hình thang cân để đảm bảo hoạt động.
• Xây dựng: Công tính chu vi, diện tích thường được sử dụng để tính số lượng vật liệu cần dùng khi xây dựng các công trình có dạng hình thang cân như mái nhà, sàn nhà,…

Hy vọng qua những thông tin trên, các bạn học sinh đã nắm rõ định nghĩa, tính chất, dấu hiệu nhận biết và ứng dụng của hình thang cân là gì. Để biết thêm nhiều công thức tính của các hình học khác, hãy theo dõi những bài viết khác của Học Thế Nào nhé.