Tìm hiểu phương trình đường tròn và công thức lập phương trình hiệu quả

Sapo: Phương trình đường tròn là một công cụ quan trọng trong hình học, giúp biểu diễn các điểm cách đều một điểm cố định. Bài viết cung cấp công thức, cách lập và các điều kiện cần thiết để nhận diện đường tròn trong không gian toán học. Nội dung phong phú, dễ hiểu sẽ hỗ trợ học sinh nắm vững kiến thức và ứng dụng hiệu quả trong bài tập.

Phương trình đường tròn là biểu thức toán học biểu diễn tập hợp các điểm cách đều tâm một khoảng bằng bán kính

Trong Hình học phẳng toán, phương trình đường tròn được xây dựng dựa trên định nghĩa hình học về đường tròn – tập hợp các điểm cách đều một điểm cố định gọi là tâm một khoảng không đổi gọi là bán kính. Phương trình này có vai trò quan trọng trong việc nghiên cứu các tính chất hình học của đường tròn.

Khi biểu diễn trên hệ trục tọa độ Oxy, phương trình đường tròn được viết dưới dạng (x – a)² + (y – b)² = R², trong đó (a,b) là tọa độ tâm và R là bán kính. Đây là dạng chuẩn tắc của phương trình, giúp ta dễ dàng xác định được vị trí tâm và độ dài bán kính của đường tròn.

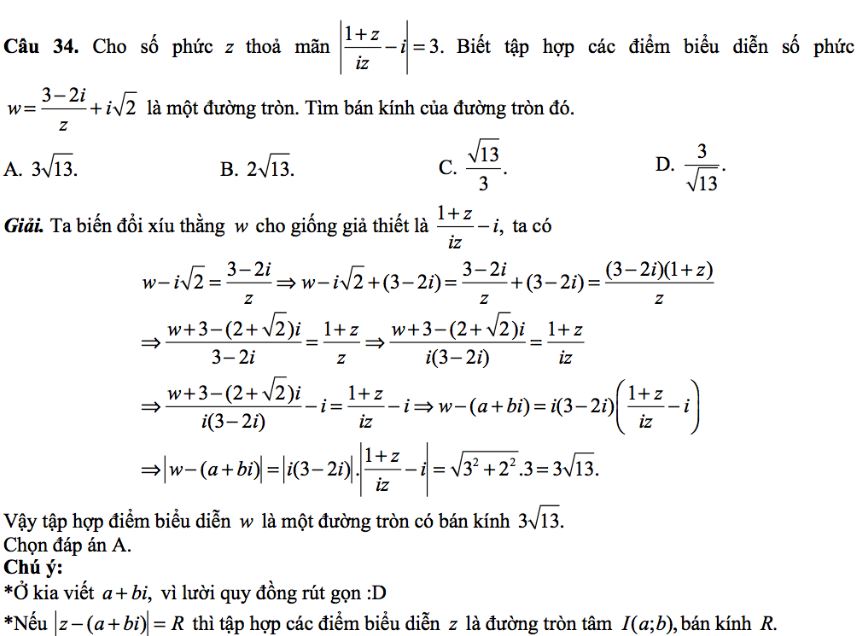
Ngoài ra, phương trình đường tròn còn có thể được viết dưới dạng tổng quát x² + y² + Dx + Ey + F = 0, với D, E, F là các hệ số thực. Dạng này thường xuất hiện trong các bài toán thực tế và đòi hỏi kỹ năng biến đổi để đưa về dạng chuẩn tắc nhằm xác định các yếu tố của đường tròn.

Các dạng phương trình đường tròn thường gặp trong toán học

Trong hình học giải tích, phương trình đường tròn có nhiều dạng biểu diễn khác nhau tùy thuộc vào mục đích sử dụng. Mỗi dạng phương trình sẽ thể hiện các đặc điểm riêng của đường tròn như tâm, bán kính hay mối quan hệ với các đường cong khác như phương trình elip.

Phương trình chính tắc của đường tròn tâm O(a,b) bán kính R

Phương trình chính tắc là dạng cơ bản nhất để biểu diễn đường tròn, có dạng (x-a)² + (y-b)² = R². Trong đó (a,b) là tọa độ tâm và R là bán kính. Dạng này tương tự như phương trình chính tắc elip nhưng đơn giản hơn do tính đối xứng.

Khi tâm đường tròn trùng với gốc tọa độ O(0,0), phương trình sẽ rút gọn thành x² + y² = R². Đây là trường hợp đặc biệt thường được sử dụng để đơn giản hóa các bài toán hình học.

Phương trình tổng quát của đường tròn

Phương trình tổng quát có dạng x² + y² + Dx + Ey + F = 0, trong đó D, E, F là các hệ số thực. Dạng này thường xuất hiện sau khi khai triển phương trình chính tắc hoặc khi giải các bài toán phức tạp.

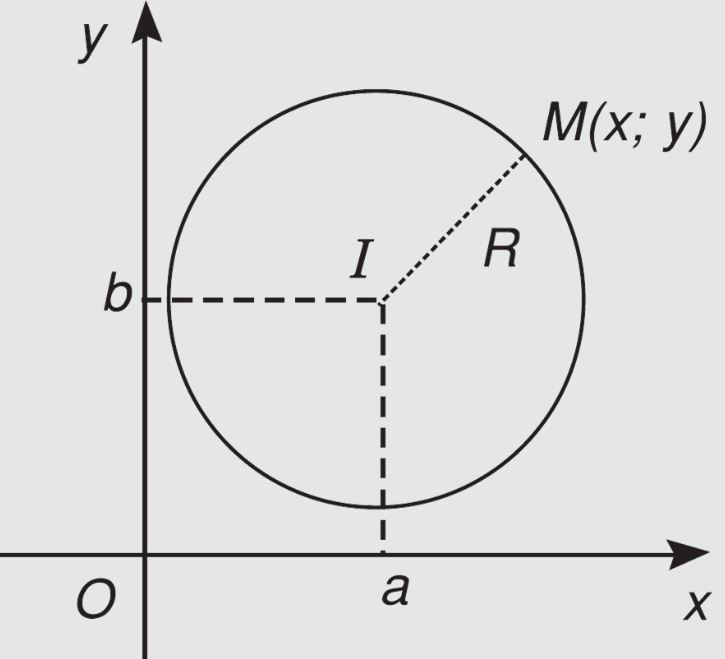
Để xác định tâm và bán kính từ phương trình tổng quát, ta có thể hoàn chỉnh bình phương để đưa về dạng chính tắc. Tâm đường tròn sẽ có tọa độ (-D/2, -E/2) và bán kính R = √((D²+E²)/4 – F).

Phương trình đường tròn dưới dạng tham số

Phương trình tham số biểu diễn mỗi điểm trên đường tròn thông qua một tham số t: x = a + R.cos(t), y = b + R.sin(t) với t ∈ [0,2π]. Dạng này đặc biệt hữu ích khi cần xác định vị trí của một điểm di chuyển trên đường tròn.

Phương trình tham số cho phép mô tả chuyển động tròn một cách trực quan và được ứng dụng rộng rãi trong vật lý, kỹ thuật. Ví dụ, khi mô phỏng chuyển động của các vật thể trong không gian hai chiều.

Cách lập phương trình đường tròn từ các yếu tố cho trước

Việc viết phương trình đường tròn đòi hỏi phải nắm vững các yếu tố cơ bản như tâm, bán kính và điểm thuộc đường tròn. Mỗi trường hợp sẽ có cách tiếp cận riêng để xác định phương trình chính xác. Dưới đây là các phương pháp cụ thể để giải quyết từng trường hợp.

Viết phương trình đường tròn khi biết tâm và bán kính

Khi có tâm I(a,b) và bán kính R, ta áp dụng định nghĩa đường tròn là tập hợp các điểm cách đều tâm một khoảng bằng bán kính. Với điểm M(x,y) bất kỳ thuộc đường tròn, khoảng cách IM = R được biểu diễn qua phương trình: (x-a)² + (y-b)² = R². Đây là dạng chuẩn của lập phương trình đường tròn.

Ví dụ với tâm I(2,3) và bán kính R=5, phương trình đường tròn là: (x-2)² + (y-3)² = 25. Phương trình này mô tả chính xác vị trí của mọi điểm thuộc đường tròn.

Lập phương trình đường tròn khi biết tâm và một điểm

Với tâm I(a,b) và điểm A(x₁,y₁) cho trước, ta xác định bán kính R chính là khoảng cách IA. Từ đó có thể áp dụng công thức tính khoảng cách giữa hai điểm để tìm R:
R = √[(x₁-a)² + (y₁-b)²]

Sau khi có bán kính, ta thay vào công thức tổng quát (x-a)² + (y-b)² = R² để có pt đường tròn cần tìm. Phương pháp này đặc biệt hiệu quả khi cần kiểm tra các điểm khác có thuộc đường tròn hay không.

Viết phương trình đường tròn đi qua 3 điểm cho trước

Để xác định phương trình đường tròn qua 3 điểm A, B, C không thẳng hàng, ta cần tìm tâm I là giao điểm của hai đường trung trực của AB và BC. Phương pháp này liên quan mật thiết đến việc chứng minh 4 điểm cùng thuộc một đường tròn.

Sau khi xác định được tọa độ tâm I, ta chọn một trong ba điểm đã cho để tính bán kính R. Cuối cùng thay I và R vào phương trình tổng quát để có phương trình đường tròn cần tìm. Phương pháp này đòi hỏi kỹ năng tính toán chính xác và kiểm tra kết quả cẩn thận.

Điều kiện để một phương trình bậc hai biểu diễn đường tròn

Để xác định một phương trình đường tròn, ta cần kiểm tra các điều kiện cụ thể về hệ số và định thức của phương trình. Việc xác định chính xác các điều kiện giúp phân biệt được phương trình đường tròn với các dạng phương trình bậc hai khác như pt trùng phương hay phương trình elip.

Một điều kiện phương trình đường tròn cần thỏa mãn dạng tổng quát ax² + ay² + bx + cy + d = 0, trong đó hệ số của x² và y² phải bằng nhau. Từ đó ta xét các điều kiện chi tiết về hệ số và định thức.

Điều kiện về hệ số của phương trình

Điều kiện tiên quyết về hệ số của phương trình là hệ số của x² và y² phải bằng nhau và khác 0. Điều này đảm bảo phương trình có dạng đối xứng qua tâm.

Khi đưa về dạng chuẩn (x – h)² + (y – k)² = R², các hệ số của x² và y² phải dương để đảm bảo đường tròn có bán kính thực. Nếu hệ số âm, phương trình sẽ không biểu diễn đường tròn thực.

Các hệ số b và c của x và y quyết định tọa độ tâm đường tròn. Chúng cần thỏa mãn điều kiện để tâm đường tròn nằm trong mặt phẳng tọa độ thực.

Điều kiện về định thức của phương trình

Định thức của ptrinh đường tròn được tính từ ma trận hệ số và phải thỏa mãn một số điều kiện đặc biệt. Cụ thể, định thức chính D phải khác 0 để đảm bảo đường tròn tồn tại.

Nếu định thức D > 0, phương trình biểu diễn một đường tròn thực với bán kính xác định. Trường hợp D = 0 cho ta một điểm, còn D < 0 cho đường tròn ảo.

Định thức phụ D₁ và D₂ giúp xác định tọa độ tâm đường tròn. Chúng cần thỏa mãn điều kiện để tâm đường tròn có tọa độ hữu hạn trong mặt phẳng tọa độ.

Ứng dụng phương trình đường tròn trong giải toán hình học

Phương trình đường tròn là công cụ quan trọng giúp giải quyết nhiều bài toán hình học phức tạp. Việc chuyển từ hình học sang đại số thông qua phương trình cho phép áp dụng các phương pháp đại số mạnh mẽ để tìm lời giải.

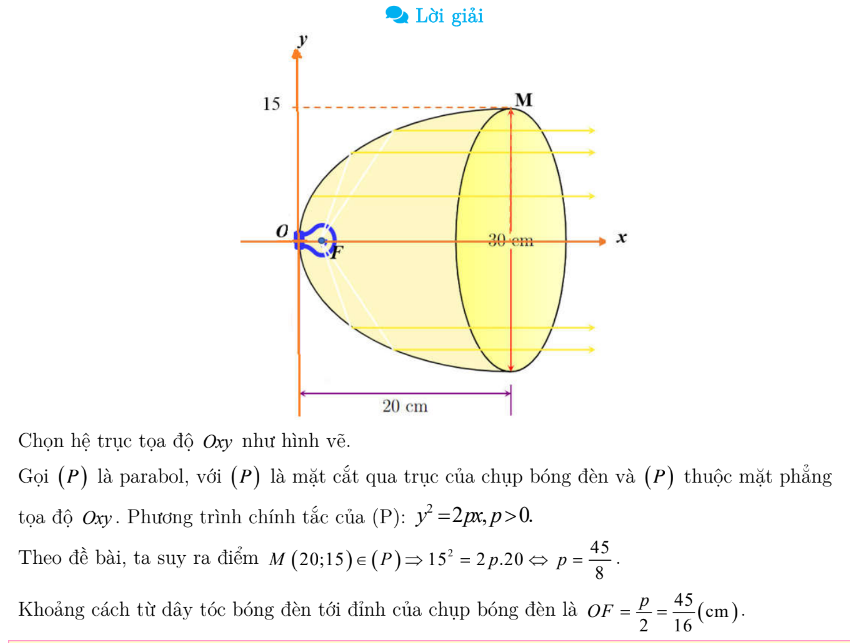
Để ứng dụng hiệu quả, cần nắm vững cách thiết lập phương trình và các kỹ thuật giải phương trình. Dưới đây là một số ứng dụng cơ bản và thường gặp nhất.

Tìm giao điểm của đường tròn với đường thẳng

Để tìm giao điểm của đường tròn và phương trình đường thẳng, ta thay tọa độ điểm từ phương trình đường thẳng vào phương trình đường tròn để được phương trình bậc 2 một ẩn.

Số nghiệm của phương trình bậc 2 cho biết số giao điểm. Nếu phương trình vô nghiệm – đường thẳng không cắt đường tròn. Nếu có một nghiệm – đường thẳng tiếp xúc với đường tròn. Nếu có hai nghiệm – đường thẳng cắt đường tròn tại hai điểm.

Từ các nghiệm tìm được, ta thay ngược vào phương trình đường thẳng để xác định tọa độ các giao điểm.

Viết phương trình tiếp tuyến của đường tròn

Viết phương trình tiếp tuyến của đường tròn có thể thực hiện qua hai phương pháp chính. Phương pháp thứ nhất là sử dụng vector pháp tuyến, khi biết một điểm thuộc tiếp tuyến.

Phương pháp thứ hai là sử dụng điều kiện tiếp xúc, khi tiếp tuyến cắt đường tròn tại đúng một điểm. Phương trình tiếp tuyến sẽ có dạng tổng quát ax + by + c = 0, trong đó các hệ số thỏa mãn điều kiện tiếp xúc.

Việc xác định chính xác phương trình tiếp tuyến giúp giải quyết nhiều bài toán về góc, khoảng cách và vị trí tương đối.

Xác định vị trí tương đối của hai đường tròn

Để xác định vị trí tương đối của hai đường tròn, ta cần so sánh khoảng cách giữa hai tâm với tổng và hiệu các bán kính. Điều này giúp xác định được hai đường tròn cắt nhau, tiếp xúc trong/ngoài hay không cắt nhau.

Khi hai đường tròn cắt nhau, ta có thể tìm tọa độ giao điểm bằng cách giải hệ phương trình của chúng. Trường hợp đặc biệt là khi một đường tròn nằm trong đường tròn kia, như tâm đường tròn nội tiếp tam giác.

Việc xác định chính xác vị trí tương đối có ý nghĩa quan trọng trong các bài toán về diện tích phần chung, góc giữa hai đường tròn và các ứng dụng thực tế.

Phương trình đường tròn là một khái niệm quan trọng trong toán học, biểu diễn tập hợp các điểm cách đều tâm một khoảng bằng bán kính. Bài viết đã trình bày các dạng phương trình, cách lập phương trình từ các yếu tố cho trước, và điều kiện để một phương trình bậc hai có thể biểu diễn đường tròn. Việc nắm rõ kiến thức về phương trình đường tròn sẽ hỗ trợ bạn trong việc giải quyết các bài toán hình học hiệu quả hơn.