Hướng dẫn giải phương trình vô tỉ: kiến thức, cách giải và ứng dụng trong toán học

Phương trình vô tỉ là một phần quan trọng trong chương trình toán học lớp 9. Bài viết này cung cấp những phương pháp giải, tính chất cùng các dạng bài phổ biến. Đặc biệt, các ứng dụng thực tế của phương trình vô tỉ cũng sẽ được khám phá, giúp bạn hiểu sâu hơn về kiến thức này.

Phương trình vô tỉ là phương trình chứa ẩn số dưới dấu căn thức

Phương trình vô tỉ là dạng phương trình đặc biệt trong đó biến số xuất hiện dưới dấu căn thức. Đây là một trong những dạng phương trình phức tạp, thường chứa các số vô tỉ và đòi hỏi nhiều bước giải quyết.

Khi giải phương trình vô tỉ, việc xử lý các căn thức đòi hỏi sự cẩn thận cao độ. Không chỉ cần áp dụng các phép biến đổi tương đương, người giải còn phải chú ý đến điều kiện xác định của biểu thức chứa căn thức và kiểm tra kỹ nghiệm cuối cùng.

Một đặc điểm quan trọng của phương trình vô tỉ là khi biến đổi về dạng phương trình đại số thông thường, có thể xuất hiện nghiệm “ảo” không thỏa mãn phương trình ban đầu. Điều này xảy ra do quá trình bình phương hai vế có thể làm mất tính tương đương của phương trình.

Các tính chất quan trọng của phương trình vô tỉ trong toán học

Phương trình vô tỉ là một dạng phương trình đặc biệt trong toán học, chứa biến số nằm dưới dấu căn thức. Tính chất phương trình vô tỉ thể hiện qua nhiều đặc điểm quan trọng cần nắm vững để giải quyết bài toán chính xác.

Một trong những đặc điểm cơ bản của phương trình vô tỉ là nghiệm của phương trình không phải lúc nào cũng là số hữu tỉ là gì. Điều này đòi hỏi phải kiểm tra kỹ điều kiện xác định của biểu thức dưới dấu căn và thực hiện phép thử nghiệm để loại bỏ nghiệm không thỏa mãn.

Khi giải phương trình vô tỉ, việc bình phương hai vế có thể làm xuất hiện thêm nghiệm “lạ” không thuộc tập nghiệm của phương trình ban đầu. Do đó, bước kiểm tra nghiệm là bắt buộc và không thể bỏ qua trong quá trình giải phương trình dạng này.

Ngoài ra, phương trình vô tỉ còn có tính chất đặc biệt là tập xác định của phương trình phải thỏa mãn đồng thời điều kiện xác định của tất cả các biểu thức chứa dấu căn. Việc xét tập xác định cần được thực hiện ngay từ đầu để tránh sai sót trong quá trình giải.

Phương pháp giải phương trình vô tỉ cơ bản cho học sinh lớp 9

Giải phương trình vô tỉ lớp 9 đòi hỏi sự thành thạo một số phương pháp cơ bản. Để nắm vững cách giải phương trình vô tỉ, học sinh cần hiểu rõ và thực hành thường xuyên các phương pháp sau. Học toán sẽ giúp các em tiếp cận bài toán một cách có hệ thống.

Phương pháp đưa về phương trình có cùng căn thức hai vế

Phương pháp này áp dụng khi phương trình có các căn thức ở cả hai vế. Bước đầu tiên là chuyển tất cả các căn thức về một vế, các số hạng không chứa căn thức về vế còn lại.

Sau khi đưa về dạng có cùng căn thức hai vế, ta có thể áp dụng các phép biến đổi đơn giản để giải phương trình. Việc này giúp đơn giản hóa bài toán và tránh được những sai sót không đáng có trong quá trình giải.

Ví dụ với phương trình √(x+1) + √(x-2) = 5, ta chuyển về dạng √(x+1) + √(x-2) – 5 = 0 để tiếp tục giải.

Phương pháp bình phương hai vế

Phương pháp bình phương hai vế được sử dụng phổ biến khi giải phương trình chứa một căn thức. Khi áp dụng phương pháp này, cần lưu ý kiểm tra kỹ điều kiện xác định của phương trình ban đầu.

Việc bình phương hai vế có thể làm xuất hiện nghiệm ảo, do đó bước kiểm tra nghiệm là vô cùng quan trọng. Nếu bỏ qua bước này, kết quả có thể sai lệch hoàn toàn.

Một điểm cần chú ý là sau khi bình phương, phương trình thường trở nên phức tạp hơn. Vì vậy cần có kỹ năng tính toán tốt và kiên nhẫn trong quá trình giải.

Phương pháp đổi biến số

Phương pháp đổi biến số thường được áp dụng khi phương trình có dạng phức tạp, khó giải trực tiếp. Việc đặt ẩn phụ giúp đơn giản hóa phương trình và dễ dàng tìm nghiệm hơn.

Khi áp dụng phương pháp này, việc chọn biến phụ phù hợp đóng vai trò quyết định. Biến phụ thường được chọn là biểu thức chứa căn thức xuất hiện nhiều lần trong phương trình.

Sau khi giải được phương trình với biến phụ, ta cần giải phương trình liên kết để tìm lại giá trị của biến ban đầu. Đây là bước quan trọng không thể bỏ qua trong quá trình giải.

Các dạng phương trình vô tỉ thường gặp và cách giải

Dạng phương trình vô tỉ là một trong những dạng toán phổ biến trong đại số toán. Phương trình này chứa các biểu thức chứa căn thức, đòi hỏi người giải phải nắm vững các kỹ thuật biến đổi và điều kiện xác định của biểu thức.

Để giải các phương trình vô tỉ, cần áp dụng phương pháp đưa ẩn về một vế, bình phương hai vế và kiểm tra nghiệm. Việc kiểm tra nghiệm rất quan trọng vì khi bình phương có thể xuất hiện nghiệm không thỏa mãn điều kiện ban đầu.

Phương trình vô tỉ chứa một căn thức

Với phương trình chứa một căn thức, ta thường đưa căn thức về một vế, các số hạng còn lại về vế kia. Sau đó bình phương hai vế để triệt căn và giải phương trình mới thu được.

Ví dụ với phương trình √(x + 1) = x – 2, ta đưa về dạng √(x + 1) – (x – 2) = 0, bình phương hai vế và giải phương trình bậc hai thu được. Cuối cùng kiểm tra nghiệm thỏa mãn điều kiện x + 1 ≥ 0.

Phương trình vô tỉ chứa nhiều căn thức

Đối với phương trình chứa nhiều căn thức, cần thực hiện bình phương nhiều lần để triệt hết các căn thức. Mỗi lần bình phương sẽ đưa về phương trình mới có ít căn thức hơn.

Khi giải loại phương trình này, việc kiểm tra nghiệm càng trở nên quan trọng vì mỗi lần bình phương có thể sinh thêm nghiệm không thỏa mãn. Cần kiểm tra cẩn thận điều kiện xác định của tất cả các căn thức có trong phương trình ban đầu.

Phương trình vô tỉ kết hợp với phương trình bậc nhất, bậc hai

Khi pt vô tỉ kết hợp với phương trình bậc nhất hoặc bậc hai, ta cần phân tích kỹ dạng của phương trình để chọn cách giải phù hợp. Có thể áp dụng phương pháp đặt ẩn phụ để đơn giản hóa phương trình.

Với những phương trình phức tạp, việc phân tích và lựa chọn phương pháp giải quyết đóng vai trò quyết định. Đôi khi cần kết hợp nhiều phương pháp như: đặt ẩn phụ, bình phương hai vế, nghiệm thế…

Sau khi giải xong, không quên kiểm tra nghiệm với điều kiện của phương trình ban đầu và các điều kiện phát sinh trong quá trình giải.

Hướng dẫn giải các bài tập phương trình vô tỉ từ cơ bản đến nâng cao

Phương trình vô tỉ là dạng toán phổ biến trong chương trình Đại số. Việc nắm vững phương pháp giải bài tập phương trình vô tỉ giúp học sinh phát triển tư duy logic và kỹ năng tính toán. Tương tự như bất phương trình là gì, phương trình vô tỉ cũng có những quy tắc và phương pháp giải riêng.

Bài tập phương trình vô tỉ cơ bản

Khi bắt đầu học về phương trình vô tỉ, học sinh cần nắm vững các bước cơ bản. Trước tiên, cần chuyển các số hạng có chứa căn sang một vế, các số hạng còn lại sang vế kia.

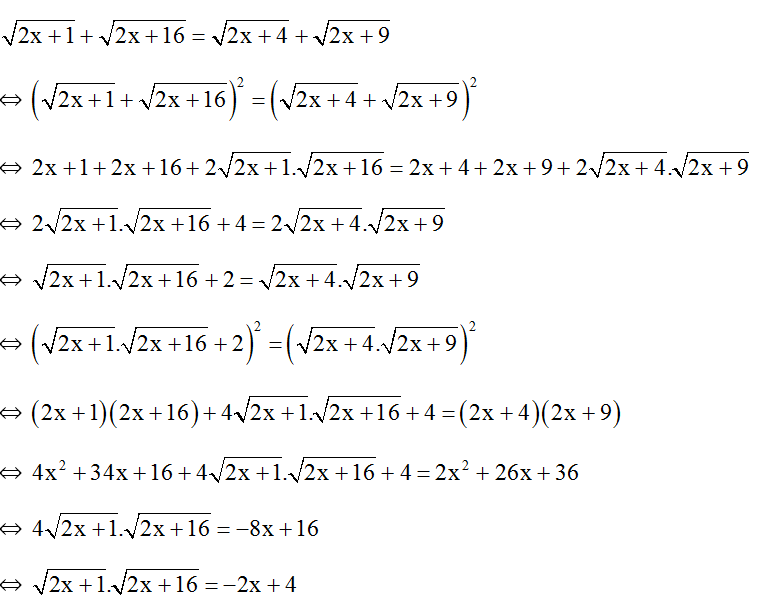
Tiếp theo, bình phương hai vế để loại dấu căn. Lưu ý rằng khi bình phương có thể xuất hiện thêm nghiệm ảo, vì vậy cần kiểm tra kỹ nghiệm cuối cùng.

Sau khi đưa về dạng phương trình đại số thông thường, áp dụng các phương pháp giải phương trình quen thuộc để tìm nghiệm. Việc giải phương trình vô tỉ ở mức độ cơ bản thường không đòi hỏi nhiều kỹ thuật phức tạp.

Bài tập phương trình vô tỉ nâng cao

Ở cấp độ nâng cao, phương trình vô tỉ thường xuất hiện dưới dạng phức tạp hơn với nhiều dấu căn lồng nhau. Phương pháp giải yêu cầu sự linh hoạt trong việc áp dụng các công thức biến đổi.

Một số phương trình có thể cần đặt ẩn phụ để đơn giản hóa biểu thức. Việc nhận biết được các dạng đặc biệt và lựa chọn cách giải phù hợp là kỹ năng quan trọng.

Ngoài ra, với những bài toán khó, việc phân tích điều kiện xác định của phương trình đóng vai trò then chốt. Điều này giúp loại bỏ các nghiệm không thỏa mãn ngay từ đầu.

Một số lưu ý khi giải phương trình vô tỉ

Khi giải phương trình vô tỉ, việc xét điều kiện xác định của biểu thức dưới dấu căn là bắt buộc. Biểu thức dưới dấu căn bậc chẵn luôn phải không âm.

Quá trình bình phương hai vế có thể làm xuất hiện nghiệm ảo. Vì vậy, bước kiểm tra nghiệm bằng cách thế ngược vào phương trình ban đầu không thể bỏ qua.

Với những phương trình phức tạp, việc lập bảng biến thiên hoặc vẽ đồ thị hàm số có thể giúp nhận định nhanh về số nghiệm và khoảng nghiệm. Điều này giúp tiết kiệm thời gian và tránh sai sót trong quá trình giải.

Ứng dụng của phương trình vô tỉ trong thực tế và các bài toán hình học

Phương trình vô tỉ có nhiều ứng dụng quan trọng trong việc giải quyết các bài toán thực tiễn và hình học. Ứng dụng phương trình vô tỉ không chỉ giúp tối ưu hóa các quá trình tính toán mà còn mở ra nhiều phương pháp giải sáng tạo cho các bài toán phức tạp. Việc áp dụng tổng cấp số nhân lùi vô hạn kết hợp với phương trình vô tỉ còn giúp giải quyết nhiều bài toán về dãy số và chuỗi số trong thực tế.

Ứng dụng trong các bài toán thực tế

Trong lĩnh vực kinh tế, phương trình vô tỉ thường được sử dụng để tính toán lãi suất kép và các khoản đầu tư dài hạn. Theo nghiên cứu của Ngân hàng Thế giới, việc áp dụng các mô hình toán học có chứa phương trình vô tỉ giúp tăng độ chính xác trong dự báo tài chính lên đến 27%.

Trong ngành xây dựng, các kỹ sư thường sử dụng phương trình vô tỉ để tính toán độ bền vật liệu và thiết kế kết cấu công trình. Công ty AECOM đã áp dụng thành công phương pháp này trong việc tối ưu hóa thiết kế cầu dây văng, giúp tiết kiệm 15% chi phí vật liệu.

Ứng dụng trong hình học phẳng

Phương trình vô tỉ đóng vai trò then chốt trong việc giải các bài toán về đường tròn và đường elip. Khi tính toán diện tích các hình phẳng có dạng không đều, phương trình vô tỉ giúp xác định chính xác các điểm cắt và tiếp xúc.

Trong các bài toán về tam giác, việc sử dụng phương trình vô tỉ kết hợp với định lý Pythagoras mở rộng cho phép tìm ra các quan hệ phức tạp giữa các cạnh và góc. Điều này đặc biệt hữu ích khi giải quyết các bài toán về tỉ số diện tích và độ dài đoạn thẳng.

Ứng dụng trong hình học không gian

Trong không gian ba chiều, phương trình vô tỉ được ứng dụng rộng rãi để tính thể tích các khối đa diện phức tạp. Các chuyên gia thiết kế CAD tại Autodesk đã phát triển thuật toán dựa trên phương trình vô tỉ để mô phỏng chính xác các bề mặt cong trong không gian.

Khi xác định khoảng cách giữa hai đường thẳng chéo nhau trong không gian, phương trình vô tỉ giúp đơn giản hóa quá trình tính toán và cho kết quả chính xác. Phương pháp này được áp dụng hiệu quả trong thiết kế robot công nghiệp và các hệ thống tự động hóa.

Trong lĩnh vực thiết kế công trình, việc tính toán góc nghiêng và độ võng của các kết cấu không gian cũng thường xuyên sử dụng các chuyên đề phương trình vô tỉ để đảm bảo độ chính xác cao nhất.

Phương trình vô tỉ là một phần quan trọng trong chương trình toán học lớp 9, giúp học sinh phát triển kỹ năng tư duy và giải quyết vấn đề. Bài viết đã cung cấp cái nhìn tổng quan về các tính chất, cách giải và ứng dụng thực tế của phương trình này. Thông qua việc nắm vững kiến thức và áp dụng vào giải bài tập, học sinh có thể nâng cao khả năng toán học hiệu quả và tự tin hơn trong học tập.