R là tập hợp số gì và ứng dụng quan trọng trong toán học hiện đại

R là tập hợp số gì? Tập R trong toán học không chỉ là một biểu tượng, mà còn là cơ sở cho nhiều kiến thức, định nghĩa và ứng dụng thú vị. Khám phá đặc điểm, tính chất và mối quan hệ của tập hợp này để hiểu rõ hơn về vai trò của nó trong số học và ứng dụng thực tế.

R là tập hợp số gì?

Tập hợp R, hay còn gọi là tập số thực, bao gồm tất cả các số có thể biểu diễn trên trục số. Đây là một khái niệm cơ bản và quan trọng trong toán học, được xây dựng từ việc mở rộng tập hợp là gì​ số tự nhiên và số hữu tỉ.

R là tập hợp số gì có thể được hiểu một cách đơn giản là tập hợp chứa mọi số hữu tỉ và vô tỉ. Điều này bao gồm các số nguyên như -2, -1, 0, 1, 2, các phân số như 1/2, 3/4, và cả những số vô tỉ như π, √2, e. Tất cả các số này đều có thể được biểu diễn chính xác trên trục số thực.

Tập R có tính chất đặc biệt là tính liên tục và đầy đủ. Điều này có nghĩa là giữa hai số thực bất kỳ luôn tồn tại vô số số thực khác, và mọi dãy Cauchy của số thực đều hội tụ về một số thực. Tính chất này làm cho R trở thành nền tảng cho nhiều lĩnh vực toán học cao cấp như giải tích và đại số.

R là số gì trong thực tế có thể được áp dụng rộng rãi trong đo lường các đại lượng vật lý như chiều dài, khối lượng, thời gian. Ví dụ, chiều cao của một người có thể là 1.75m, nhiệt độ phòng có thể là 25.6°C – đây đều là những số thực được sử dụng để mô tả chính xác các đại lượng trong thế giới thực.

Các tập hợp số cơ bản trong toán học và vị trí của tập R

Trong toán học, các tập hợp số được xây dựng và mở rộng dần từ đơn giản đến phức tạp, tạo thành một hệ thống chặt chẽ. Mỗi tập hợp số có những đặc điểm và ứng dụng riêng trong việc giải quyết các bài toán thực tế.

Các tập hợp số được sắp xếp theo thứ tự bao hàm, trong đó tập số thực R đóng vai trò trung tâm và là nền tảng cho nhiều phép toán quan trọng. Việc hiểu rõ mối quan hệ giữa các tập hợp số giúp nắm vững bản chất của chúng và áp dụng hiệu quả vào thực tiễn.

Tập số tự nhiên (N) và số nguyên (Z)

Tập hợp số tự nhiên bao gồm các số dùng để đếm, bắt đầu từ 0 và tăng dần vô hạn. Tập này được sử dụng rộng rãi trong cuộc sống hàng ngày, từ việc đếm số lượng đến tính toán đơn giản.

Tập hợp số nguyên mở rộng từ tập số tự nhiên bằng cách thêm vào các số âm. Tập này đóng vai trò quan trọng trong việc biểu diễn các đại lượng có thể âm hoặc dương như nhiệt độ, độ cao so với mực nước biển.

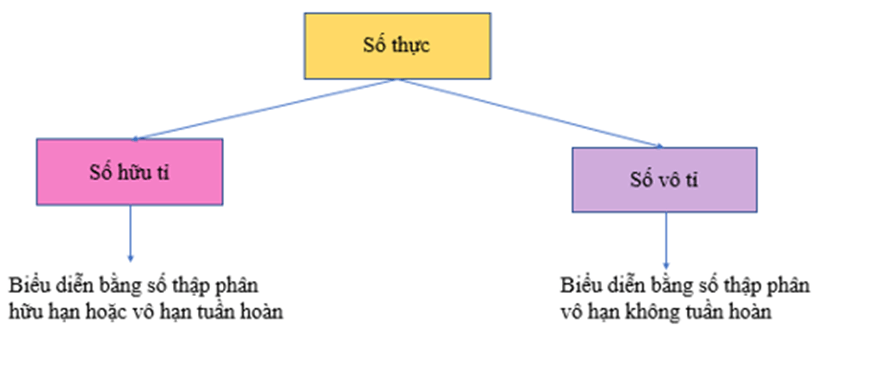
Tập số hữu tỉ (Q) và vô tỉ

Tập hợp số hữu tỉ bao gồm các số có thể biểu diễn dưới dạng phân số p/q với p, q là số nguyên và q khác 0. Tập này giúp giải quyết nhiều bài toán thực tế liên quan đến phân chia, tỷ lệ.

Tập hợp số vô tỉ bổ sung cho tập số hữu tỉ những số không thể biểu diễn dưới dạng phân số, như π hay √2. Các số vô tỉ xuất hiện tự nhiên trong hình học và các phép tính liên quan đến căn bậc hai.

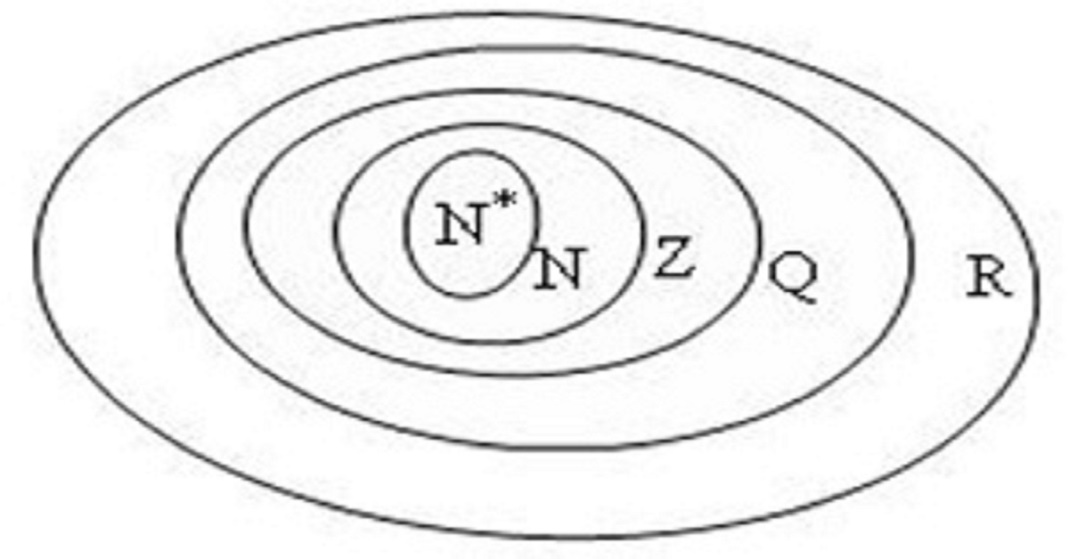
Tập số thực R và mối quan hệ với các tập hợp khác

Tập hợp số thực là sự kết hợp của tập số hữu tỉ và vô tỉ, tạo thành một tập hợp liên tục và đầy đủ. Tập R có tính chất đóng đối với các phép toán cơ bản và được biểu diễn trực quan trên trục số.

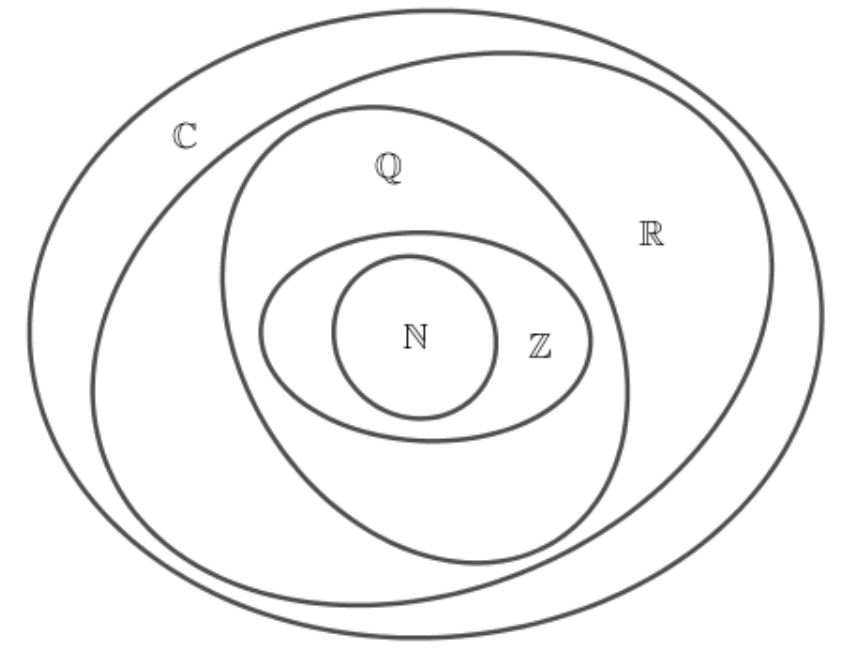
Mối quan hệ giữa các tập hợp số tuân theo quy luật bao hàm: N ⊂ Z ⊂ Q ⊂ R. Mỗi tập con kế thừa tất cả tính chất của tập cha và bổ sung thêm các phần tử mới với những đặc điểm riêng.

Tập số phức (C) – Mở rộng từ tập R

Tập hợp số phức được tạo ra để giải quyết những bài toán không có nghiệm trong tập số thực, như phương trình x² + 1 = 0. Modun số phức​ mở rộng khả năng tính toán và ứng dụng trong nhiều lĩnh vực như điện tử, cơ học lượng tử.

Số phức có dạng tổng quát a + bi, trong đó a, b là các số thực và i là đơn vị ảo thỏa mãn i² = -1. Tập C hoàn thiện hệ thống số học cơ bản và đóng vai trò quan trọng trong toán học hiện đại.

Đặc điểm và tính chất quan trọng của tập hợp số thực R

Tập hợp R là gì? R là tập hợp số thực bao gồm tất cả các số hữu tỉ và số vô tỉ. Tập hợp r là gì và có những đặc điểm nào? Đây là tập hợp vô hạn không đếm được, có tính chất đầy đủ, liên tục và có trật tự.

Tập R có vai trò quan trọng trong toán học và ứng dụng thực tiễn. Ví dụ như 1e bằng bao nhiêu là một số vô tỉ thuộc tập R, được sử dụng rộng rãi trong tính toán lãi kép và các bài toán tăng trưởng.

Tính đầy đủ của tập R

Tính đầy đủ của tập R thể hiện ở việc không có “lỗ hổng” giữa các số thực. Mọi dãy Cauchy trong R đều hội tụ về một số thực trong R. Điều này có nghĩa là với bất kỳ hai số thực a và b, luôn tồn tại vô số số thực nằm giữa chúng.

Tính chất này giúp ta có thể biểu diễn chính xác mọi khoảng cách, độ dài trong không gian thực. Ví dụ, độ dài cạnh huyền của tam giác vuông cân cạnh góc vuông bằng 1 là √2 – một số vô tỉ thuộc R.

Tính liên tục và trật tự của R

Tính liên tục của R thể hiện qua khả năng biểu diễn mọi điểm trên trục số thực mà không có khoảng trống. Điều này cho phép ta vẽ được đường thẳng liên tục không đứt đoạn.

Về trật tự, R là tập hợp có thứ tự toàn phần, nghĩa là với hai số thực bất kỳ, ta luôn có thể so sánh được chúng. Tính chất này rất quan trọng trong việc sắp xếp, so sánh các đại lượng trong thực tế.

Các phép toán cơ bản trên R

Các phép toán cộng, trừ, nhân, chia (trừ chia cho 0) trên R đều cho kết quả thuộc R. Tính chất đóng này đảm bảo tính ổn định khi thực hiện các phép tính.

Trong thực tế, các phép toán này tuân theo các quy tắc kết hợp, giao hoán và phân phối. Điều này giúp đơn giản hóa các phép tính phức tạp và là nền tảng cho đại số cao cấp.

Ngoài ra, R cũng đóng đối với phép khai căn bậc chẵn của số dương và phép lũy thừa với số mũ hữu tỉ. Các tính chất này mở rộng khả năng ứng dụng của R trong nhiều lĩnh vực khoa học kỹ thuật.

Các tập con quan trọng của R và ứng dụng

Tập hợp R gồm tất cả các số thực và có nhiều tập con đặc biệt với các tính chất riêng biệt. Việc phân loại và nghiên cứu các tập con này có ý nghĩa quan trọng trong toán học và ứng dụng thực tiễn. Tập R là tập gồm vô số phần tử với cấu trúc phức tạp, do đó việc chia thành các tập hợp con nhỏ hơn giúp dễ dàng nghiên cứu và áp dụng.

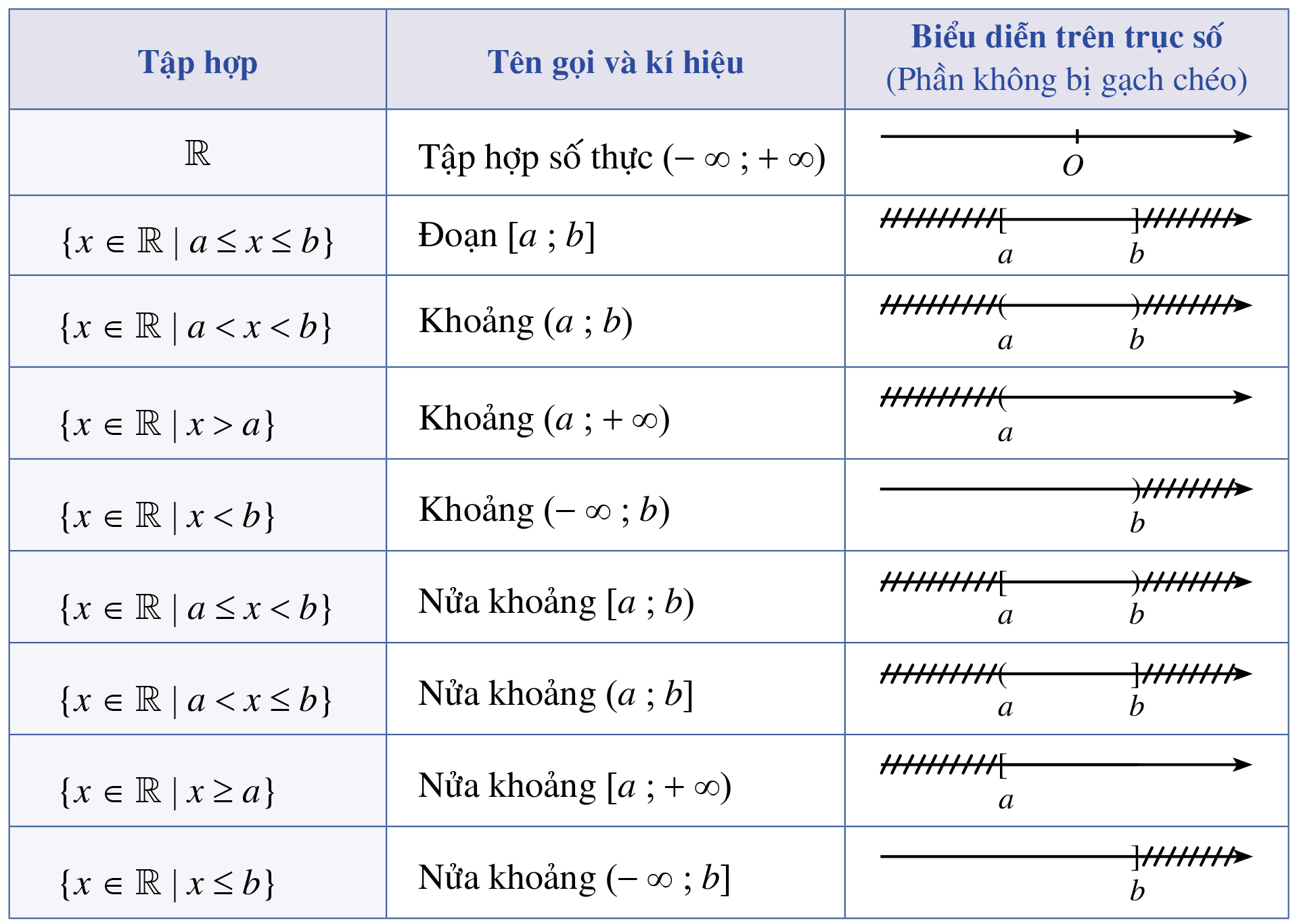
Khoảng, đoạn và nửa đoạn

Khoảng là tập hợp tất cả các số thực nằm giữa hai số cho trước. Khoảng có thể mở hoặc đóng tùy thuộc vào việc bao gồm các điểm đầu mút hay không. Ví dụ, khoảng (0,1) chỉ bao gồm các số thực lớn hơn 0 và nhỏ hơn 1.

Đoạn là khoảng đóng bao gồm cả hai điểm đầu mút. Chẳng hạn đoạn [2,5] chứa tất cả các số thực từ 2 đến 5, bao gồm cả 2 và 5. Đoạn thường được sử dụng để tính toán các ước số trong một phạm vi xác định.

Nửa đoạn là khoảng chỉ đóng ở một đầu mút. Ví dụ [0,1) bao gồm số 0 nhưng không bao gồm số 1.

Tập hợp bị chặn và không bị chặn

Tập hợp bị chặn là tập hợp nằm gọn trong một khoảng hữu hạn. Điều này có nghĩa tồn tại hai số thực M và m sao cho mọi phần tử x của tập đều thỏa mãn m ≤ x ≤ M. Ví dụ như đoạn [0,1] là một tập bị chặn.

Ngược lại, tập không bị chặn là tập có thể chứa các phần tử với giá trị tuyệt đối lớn tùy ý. Tập số nguyên Z là một ví dụ điển hình về tập không bị chặn, vì với mọi số M > 0, luôn tồn tại số nguyên có giá trị tuyệt đối lớn hơn M.

Tập hợp đóng và tập hợp mở

Tập hợp đóng là tập hợp chứa tất cả các điểm giới hạn của nó. Một điểm được gọi là điểm giới hạn nếu mọi lân cận của nó đều chứa ít nhất một điểm thuộc tập hợp khác với chính nó. Ví dụ đoạn [0,1] là một tập đóng.

Tập hợp mở là tập hợp mà với mỗi điểm thuộc tập, tồn tại một lân cận của điểm đó nằm hoàn toàn trong tập. Khoảng (0,1) là một tập mở. Tập hợp vừa không đóng vừa không mở cũng tồn tại, như nửa đoạn [0,1).

Việc phân biệt giữa tập đóng và tập mở có ý nghĩa quan trọng trong giải tích, đặc biệt trong nghiên cứu về tính liên tục của hàm số.

Ứng dụng của tập R trong giải toán và thực tế

Tập hợp R có vai trò quan trọng trong việc biểu diễn các đại lượng liên tục trong toán học và thực tế. Khi giải quyết các bài toán phức tạp, việc hiểu rõ “r là tập hợp số gì” sẽ giúp chúng ta áp dụng hiệu quả vào nhiều lĩnh vực khác nhau.

Giải phương trình và bất phương trình

Tập số thực đóng vai trò then chốt trong việc giải các phương trình và bất phương trình. Việc nắm vững các tính chất của tập R giúp học sinh dễ dàng tìm ra nghiệm chính xác.

Khi giải các bài toán phức tạp, Dạy toán trực tuyến là phương pháp hiệu quả giúp học sinh hiểu sâu hơn về cách vận dụng tập số thực. Thông qua các bài tập thực hành, học sinh sẽ thành thạo trong việc xác định miền nghiệm và biện luận kết quả.

Ứng dụng trong hình học và đại số

Trong hình học, tập R được sử dụng để biểu diễn độ dài, diện tích và thể tích của các hình. Việc tính toán chính xác các đại lượng này đòi hỏi hiểu biết sâu sắc về tính chất của số thực.

Đối với đại số, tập số thực là nền tảng để xây dựng các khái niệm về hàm số, giới hạn và đạo hàm. Các phép toán trên tập R giúp giải quyết nhiều bài toán phức tạp trong giải tích và đại số tuyến tính.

Ứng dụng trong đời sống thực tế

Trong kinh tế, tập số thực được sử dụng để tính toán lãi suất, giá trị tài sản và các chỉ số tài chính. Các nhà kinh tế thường xuyên vận dụng các tính chất của R để phân tích và dự báo xu hướng thị trường.

Trong khoa học kỹ thuật, tập R giúp đo lường chính xác các đại lượng vật lý như nhiệt độ, áp suất và tốc độ. Các kỹ sư sử dụng kiến thức về số thực để thiết kế và vận hành máy móc, thiết bị với độ chính xác cao.

Ngành xây dựng cũng áp dụng tập số thực trong việc tính toán kết cấu và thiết kế công trình. Việc đảm bảo độ chính xác trong các phép đo và tính toán góp phần tạo nên những công trình an toàn, bền vững.

Khi nói đến r là tập hợp số gì, chúng ta hiểu rằng tập R đại diện cho tập hợp số thực, bao gồm tất cả các số hữu tỉ và vô tỉ. Tập hợp này không chỉ quan trọng trong toán học mà còn có nhiều ứng dụng trong thực tiễn. Việc nắm rõ khái niệm này cùng các tập hợp liên quan sẽ giúp bạn tự tin hơn trong việc giải quyết các bài toán khó và áp dụng vào đời sống hàng ngày.