Kiến thức và định nghĩa về số chính phương trong toán học hiệu quả

Số chính phương là gì? Đây là một khái niệm quan trọng trong toán học, giúp bạn hiểu rõ hơn về mối liên hệ giữa các số và phép tính bình phương. Bài viết sẽ cung cấp các định nghĩa, tính chất nổi bật cũng như ví dụ cụ thể để hình dung rõ nét hơn về số chính phương trong dãy số tự nhiên. Bạn sẽ tìm thấy những hướng dẫn chi tiết cùng bài tập thực hành hữu ích.

Số chính phương là gì?

Số chính phương là gì – đó là một số nguyên dương được tạo thành từ bình phương của một số tự nhiên khác. Nói cách khác, khi ta nhân một số với chính nó, kết quả thu được sẽ là một số chính phương.

Trong tập hợp các số tự nhiên​, số chính phương là số gì có thể dễ dàng nhận biết thông qua phép tính căn bậc hai. Nếu căn bậc hai của một số cho kết quả là số nguyên, số đó chính là số chính phương. Ví dụ: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 là các số chính phương vì chúng lần lượt bằng 1², 2², 3², 4², 5², 6², 7², 8², 9², 10².

Số chính phương là j mà nhiều người thắc mắc có thể hiểu đơn giản qua ví dụ: Khi ta có một hình vuông với cạnh là số nguyên, diện tích của hình vuông đó sẽ là một số chính phương. Điều này giải thích tại sao chính phương là gì lại có mối liên hệ mật thiết với hình học và được ứng dụng rộng rãi trong toán học.

Trong thực tế, số chính phương xuất hiện phổ biến trong kiến trúc và thiết kế. Ví dụ như khi thiết kế gạch lát nền, người ta thường sử dụng gạch hình vuông với kích thước 20x20cm, 30x30cm, 40x40cm – tất cả đều tạo ra diện tích là các số chính phương: 400, 900, 1600 cm².

Cách xác định và tính chất của số chính phương trong toán học

Số chính phương là một khái niệm quan trọng trong toán học, được sử dụng rộng rãi trong nhiều lĩnh vực từ đại số đến hình học. Việc hiểu rõ về số chính phương giúp giải quyết nhiều bài toán phức tạp và ứng dụng thực tiễn. Tương tự như số lập phương là gì, số chính phương cũng có những đặc điểm và quy luật riêng.

Định nghĩa và cách nhận biết số chính phương

Số chính phương là số tự nhiên được tạo thành từ bình phương của một số tự nhiên khác. Ví dụ, số 16 là số chính phương vì 16 = 4², số 25 là số chính phương vì 25 = 5². Để xác định một số có phải là số chính phương hay không, ta có thể lấy căn bậc hai của số đó và kiểm tra xem kết quả có phải là số nguyên hay không.

Trong thực tế, việc nhận biết định nghĩa số chính phương thường được áp dụng trong nhiều tình huống. Chẳng hạn như khi tính diện tích hình vuông, khi một cạnh có độ dài là số nguyên, diện tích thu được sẽ là một số chính phương. Điều này có mối liên hệ chặt chẽ với phương sai là gì trong thống kê.

Các tính chất quan trọng của số chính phương

Tính chất số chính phương bao gồm nhiều đặc điểm độc đáo. Tích của hai số chính phương là một số chính phương. Ví dụ: 4 (= 2²) × 9 (= 3²) = 36 (= 6²). Số chính phương luôn là số không âm và có số chữ số chẵn sau số 0 ở dạng phân tích thừa số nguyên tố.

Một tính chất thú vị khác là khoảng cách giữa hai số chính phương liên tiếp không bằng nhau và tăng dần. Chẳng hạn, từ 1 đến 4 cách 3 đơn vị, từ 4 đến 9 cách 5 đơn vị, từ 9 đến 16 cách 7 đơn vị. Quy luật này được ứng dụng trong nhiều bài toán về dãy số và cấp số.

Mối quan hệ giữa số chính phương và phép bình phương

Phép bình phương và số chính phương có mối quan hệ mật thiết, không thể tách rời. Khi một số được bình phương, kết quả thu được sẽ là một số chính phương. Điều này tạo nên một ánh xạ một – một từ tập hợp số tự nhiên sang tập hợp các số chính phương.

Trong hình học, mối quan hệ này thể hiện rõ qua diện tích hình vuông. Khi cạnh hình vuông tăng thêm 1 đơn vị, diện tích tăng theo quy luật của số chính phương. Đây là cơ sở để giải quyết nhiều bài toán về tối ưu hóa diện tích và chu vi trong thực tế.

Các ví dụ minh họa về số chính phương trong dãy số tự nhiên

Các số chính phương là những số được tạo thành từ bình phương của một số nguyên. Chúng xuất hiện thường xuyên trong toán học và có nhiều ứng dụng thực tế trong kiến trúc, thiết kế và khoa học máy tính.

Để hiểu rõ hơn về các số chính phương, ta sẽ phân tích chi tiết các trường hợp cụ thể và cách xác định chúng trong dãy số tự nhiên.

Dãy số chính phương từ 1 đến 100

Trong khoảng từ 1 đến 100, các số chính phương được tạo thành từ bình phương của các số từ 1 đến 10. Cụ thể:

• 1 = 1²
• 4 = 2²
• 9 = 3²
• 16 = 4²
• 25 = 5²
• 36 = 6²
• 49 = 7²
• 64 = 8²
• 81 = 9²
• 100 = 10²

Mỗi số trong dãy này đều có một mối quan hệ đặc biệt với căn bậc hai của chính nó, tạo nên tính đối xứng hoàn hảo trong toán học.

Phân tích và chứng minh 1 là số chính phương

1 có phải số chính phương không là câu hỏi thường gặp. Để chứng minh, ta xét các yếu tố sau:

Số 1 là bình phương của chính nó (1 = 1²), đồng thời cũng là bình phương của số -1 (1 = (-1)²). Điều này khẳng định 1 là số chính phương nhỏ nhất trong tập hợp số tự nhiên, số 0 có phải là số nguyên dương không.

Tính chất đặc biệt này khiến số 1 trở thành một trường hợp độc đáo trong lý thuyết số học.

Bảng các số chính phương thường gặp

Các số chính phương thường xuất hiện trong nhiều bài toán và ứng dụng thực tế. Theo nghiên cứu của Viện Toán học Việt Nam, những số chính phương phổ biến nhất bao gồm:

• 100 (10²): Thường dùng trong tính toán phần trăm
• 144 (12²): Phổ biến trong đo lường
• 400 (20²): Áp dụng trong thiết kế kiến trúc
• 625 (25²): Sử dụng trong tính toán thống kê

Các số này có vai trò quan trọng trong việc giải quyết các bài toán thực tế và ứng dụng trong nhiều lĩnh vực khác nhau.

Phương pháp giải bài tập về số chính phương

Để giải các bài tập số chính phương hiệu quả, cần nắm vững định nghĩa và tính chất cơ bản. Số chính phương là số tự nhiên có dạng n2, trong đó n là một số tự nhiên. Việc áp dụng các phương pháp giải phù hợp sẽ giúp giải nhanh và chính xác các dạng bài tập khác nhau.

Khi giải toán về số chính phương, việc kết hợp kiến thức đại số đại cương với các tính chất đặc trưng sẽ giúp tìm ra lời giải tối ưu. Đặc biệt trong các bài toán phức tạp, việc vận dụng linh hoạt bất phương trình bậc nhất hai ẩn thường mang lại hiệu quả cao.

Các dạng bài tập thường gặp

Việc cách nhận biết số chính phương là kỹ năng quan trọng để giải các dạng bài tập phổ biến. Dạng bài tập kiểm tra một số có phải số chính phương hay không thường xuất hiện trong các đề thi. Ngoài ra còn có dạng tìm số chính phương trong khoảng cho trước và dạng chứng minh tính chất của số chính phương.

Dạng bài tập về tổng, hiệu, tích của các số chính phương cũng thường xuyên xuất hiện. Các bài toán này đòi hỏi sự kết hợp giữa tính chất số học và đại số để giải quyết hiệu quả.

Công thức và cách tính nhanh

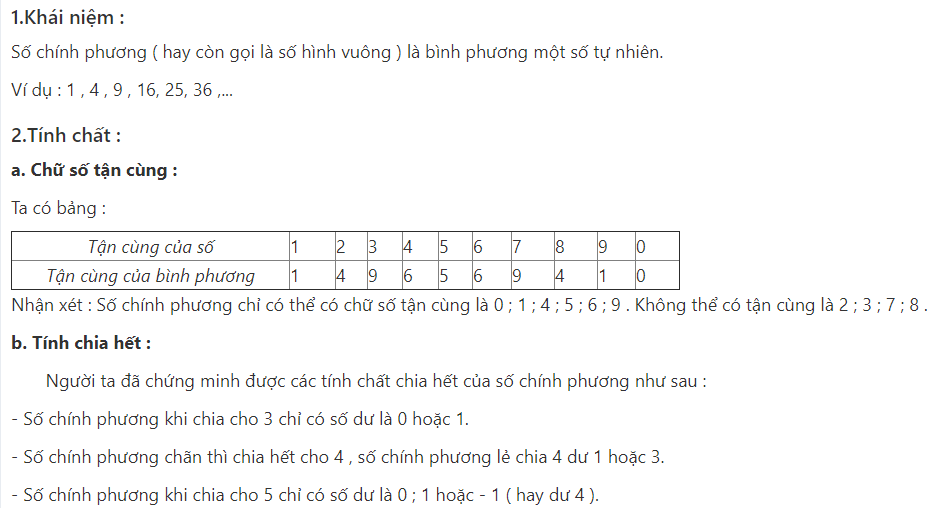
Công thức số chính phương cơ bản là n2 với n là số tự nhiên. Để tính nhanh, có thể áp dụng một số quy tắc như: số chính phương luôn có chữ số tận cùng là 0, 1, 4, 5, 6, 9. Ngoài ra, tổng các chữ số của một số chính phương khi chia cho 9 sẽ có số dư là 0, 1, 4, 7.

Một phương pháp tính nhanh khác là sử dụng bảng số chính phương từ 1 đến 100 và nhận biết quy luật. Điều này giúp tiết kiệm thời gian trong các bài tập yêu cầu tìm số chính phương gần nhất.

Hướng dẫn giải chi tiết các bài tập mẫu

Các ứng dụng số chính phương trong giải toán rất đa dạng. Ví dụ với bài toán tìm số chính phương trong khoảng [a,b], ta thực hiện các bước: lấy căn bậc hai của a và b, làm tròn lên số nguyên gần nhất, sau đó bình phương các số trong khoảng tìm được.

Với bài toán chứng minh một số là số chính phương, phương pháp phân tích thừa số nguyên tố thường được áp dụng. Nếu các thừa số nguyên tố xuất hiện với số mũ chẵn, số đó chắc chắn là số chính phương.

Trong các bài toán phức tạp hơn như tìm số chính phương thỏa mãn điều kiện cho trước, việc kết hợp các phương pháp và tính chất sẽ giúp tìm ra lời giải tối ưu nhất.

Số chính phương là một khái niệm thú vị trong toán học, đóng vai trò quan trọng trong nhiều lĩnh vực. Khi nắm bắt rõ số chính phương là gì, bạn sẽ hiểu cách xác định, các tính chất cũng như ứng dụng của chúng trong bài tập. Các ví dụ cụ thể từ 1 đến 100 giúp tăng cường khả năng nhận diện và phân tích. Việc hiểu danh sách các số chính phương sẽ hỗ trợ bạn trong việc giải quyết các bài tập liên quan một cách nhanh chóng và hiệu quả.