Khái niệm và quy tắc tìm số liền trước và số liền sau trong toán học

Số liền trước và số liền sau là hai khái niệm quan trọng trong toán học, đặc biệt trong số tự nhiên. Việc nắm rõ cách xác định và ứng dụng chúng sẽ giúp học sinh phát triển tư duy logic. Bài viết này sẽ đưa ra quy tắc, bài tập và phương pháp giải chi tiết, hỗ trợ việc học toán hiệu quả cho mọi cấp độ.

Số liền trước và số liền sau là hai số tự nhiên đứng cạnh nhau trên tia số

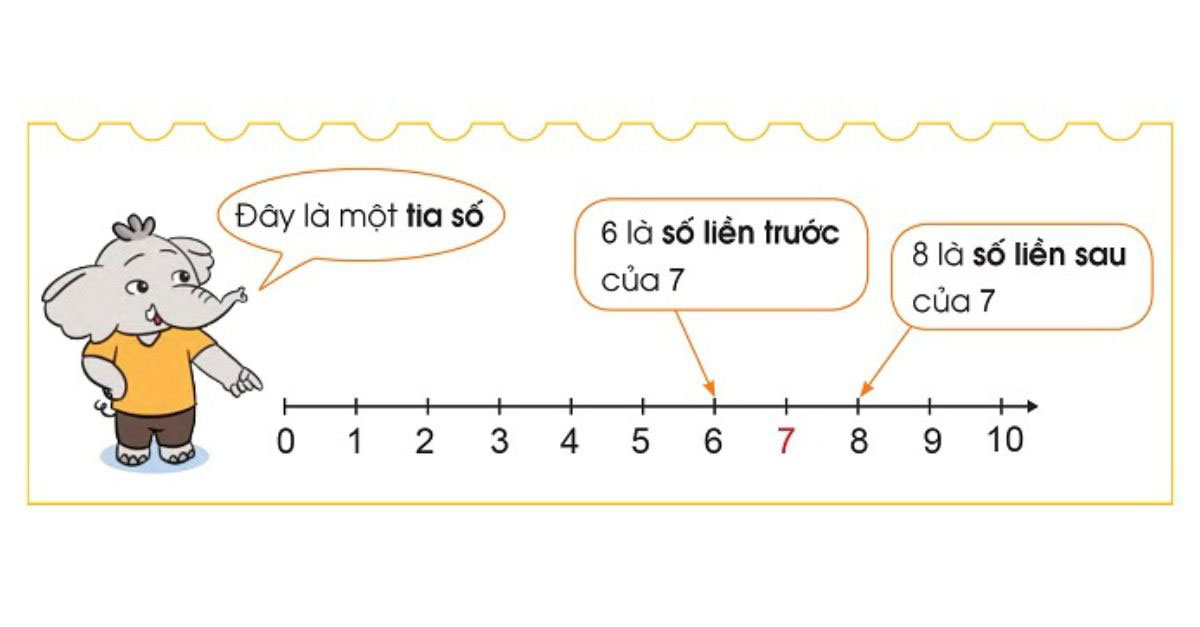
Trên tia số tự nhiên, số liền trước và số liền sau là hai số tự nhiên liên tiếp, có hiệu số bằng 1. Số liền trước luôn nhỏ hơn số liền sau một đơn vị. Ví dụ, với số 5, số liền trước là 4 và số liền sau là 6.

Khi xét một số tự nhiên bất kỳ n, số liền trước của nó được xác định bằng cách lấy n trừ đi 1 (n-1), còn số liền sau được xác định bằng cách lấy n cộng thêm 1 (n+1). Điều này áp dụng cho mọi số tự nhiên, ngoại trừ số 0 – số này chỉ có số liền sau là 1 mà không có số liền trước.

Việc xác định số liền trước và số liền sau có ý nghĩa quan trọng trong toán học, đặc biệt khi giải các bài toán về dãy số, tìm quy luật số hay thực hiện các phép tính cộng trừ cơ bản. Chẳng hạn như trong phép đếm ngược, ta cần xác định số liền trước để biết số nào sẽ được đếm tiếp theo.

Cách xác định số liền trước và số liền sau của một số tự nhiên trên tia số

Trên tia số lớp 2, các số tự nhiên được sắp xếp theo thứ tự từ nhỏ đến lớn, cách đều nhau một đơn vị. Điều này giúp ta dễ dàng xác định số liền trước và số liền sau của một số bất kỳ.

Khi quan sát một số tự nhiên trên tia số, ta có thể thấy số liền trước là gì – đó chính là số nhỏ hơn số đang xét một đơn vị. Ví dụ, số liền trước của 5 là 4, số liền trước của 10 là 9. Tương tự như cách các số vô tỉ kí hiệu là gì được biểu diễn trên trục số, việc xác định số liền trước giúp học sinh hiểu rõ hơn về trật tự của các số.

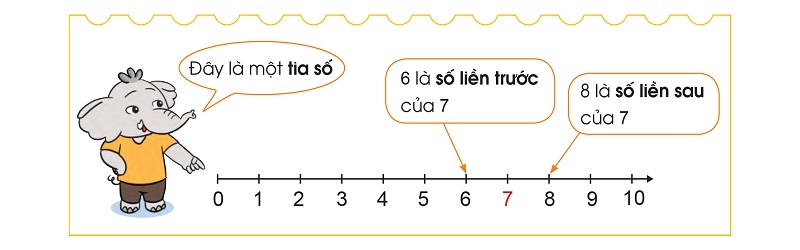
Số liền sau là gì được xác định bằng cách cộng thêm một đơn vị vào số đang xét. Chẳng hạn, số liền sau của 7 là 8, số liền sau của 15 là 16. Việc nắm vững cách xác định số liền trước và số liền sau sẽ giúp học sinh thực hiện tốt các phép tính cộng trừ và so sánh các số tự nhiên một cách chính xác.

Quy tắc cơ bản để tìm số liền trước và số liền sau trong dãy số tự nhiên

Trong dãy số tự nhiên, việc xác định số liền trước và số liền sau tuân theo một quy tắc đơn giản và nhất quán. Mỗi số tự nhiên đều có mối quan hệ chặt chẽ với các số xung quanh nó theo một trật tự nhất định.

Để áp dụng quy tắc số một cách hiệu quả, cần nắm vững nguyên lý cơ bản về tính liên tục của dãy số tự nhiên. Mỗi số trong dãy đều có vị trí xác định và không thể thay đổi, tạo nên tính ổn định trong việc xác định các số liền kề.

Cách tìm số liền trước và liền sau có thể được áp dụng cho mọi số tự nhiên, từ số nhỏ nhất đến số lớn nhất. Điều quan trọng là phải hiểu rõ mối quan hệ giữa các số để áp dụng quy tắc chính xác.

Số liền trước luôn nhỏ hơn số đang xét 1 đơn vị

Khi xác định số liền trước của một số tự nhiên, ta chỉ cần lấy số đó trừ đi 1 đơn vị. Đây là quy tắc bất biến và áp dụng cho tất cả các số tự nhiên lớn hơn 0.

Ví dụ: Với số 15, số liền trước sẽ là 14 (15 – 1 = 14)
Với số 100, số liền trước sẽ là 99 (100 – 1 = 99)

Lưu ý rằng số 0 là số tự nhiên nhỏ nhất nên không có số liền trước trong dãy số tự nhiên.

Số liền sau luôn lớn hơn số đang xét 1 đơn vị

Để tìm số liền sau của một số tự nhiên, ta cộng thêm 1 đơn vị vào số đó. Quy tắc này áp dụng cho mọi số tự nhiên mà không có ngoại lệ.

Trong thực tế, việc xác định số liền sau thường được sử dụng trong nhiều tình huống như đánh số thứ tự, tính toán tuần tự hay lập trình máy tính.

Với tính chất này, ta có thể dễ dàng xác định số liền sau của bất kỳ số tự nhiên nào bằng phép cộng đơn giản với 1.

Ứng dụng trong bài toán so sánh các số tự nhiên

Hiểu biết về số liền trước và liền sau giúp việc so sánh các số tự nhiên trở nên dễ dàng hơn. Khi so sánh hai số tự nhiên, ta có thể dựa vào vị trí tương đối của chúng trong dãy số.

Trong giảng dạy toán học, giáo viên thường sử dụng khái niệm số liền trước và liền sau để giúp học sinh hiểu rõ hơn về trật tự của các số tự nhiên. Phương pháp này đặc biệt hiệu quả khi dạy học sinh lớp đầu cấp.

Ngoài ra, việc nắm vững các quy tắc này còn hỗ trợ giải quyết nhiều dạng bài tập phức tạp hơn như tìm số lớn nhất, nhỏ nhất trong một dãy số hay sắp xếp các số theo thứ tự tăng dần, giảm dần.

Bài tập và phương pháp giải về số liền trước và số liền sau

Việc nắm vững kiến thức về số liền trước và số liền sau là nền tảng quan trọng giúp học sinh phát triển tư duy toán học. Các bài tập về chủ đề này thường xuất hiện trong chương trình toán tiểu học và được triển khai theo nhiều dạng khác nhau.

Để giải các bài tập toán liên quan đến số liền trước và liền sau, học sinh cần hiểu rõ quy tắc: số liền trước nhỏ hơn số đang xét 1 đơn vị, số liền sau lớn hơn số đang xét 1 đơn vị. Tương tự như cách áp dụng mệnh đề kéo theo, việc nắm vững quy tắc này sẽ giúp giải quyết nhanh chóng các dạng bài tập.

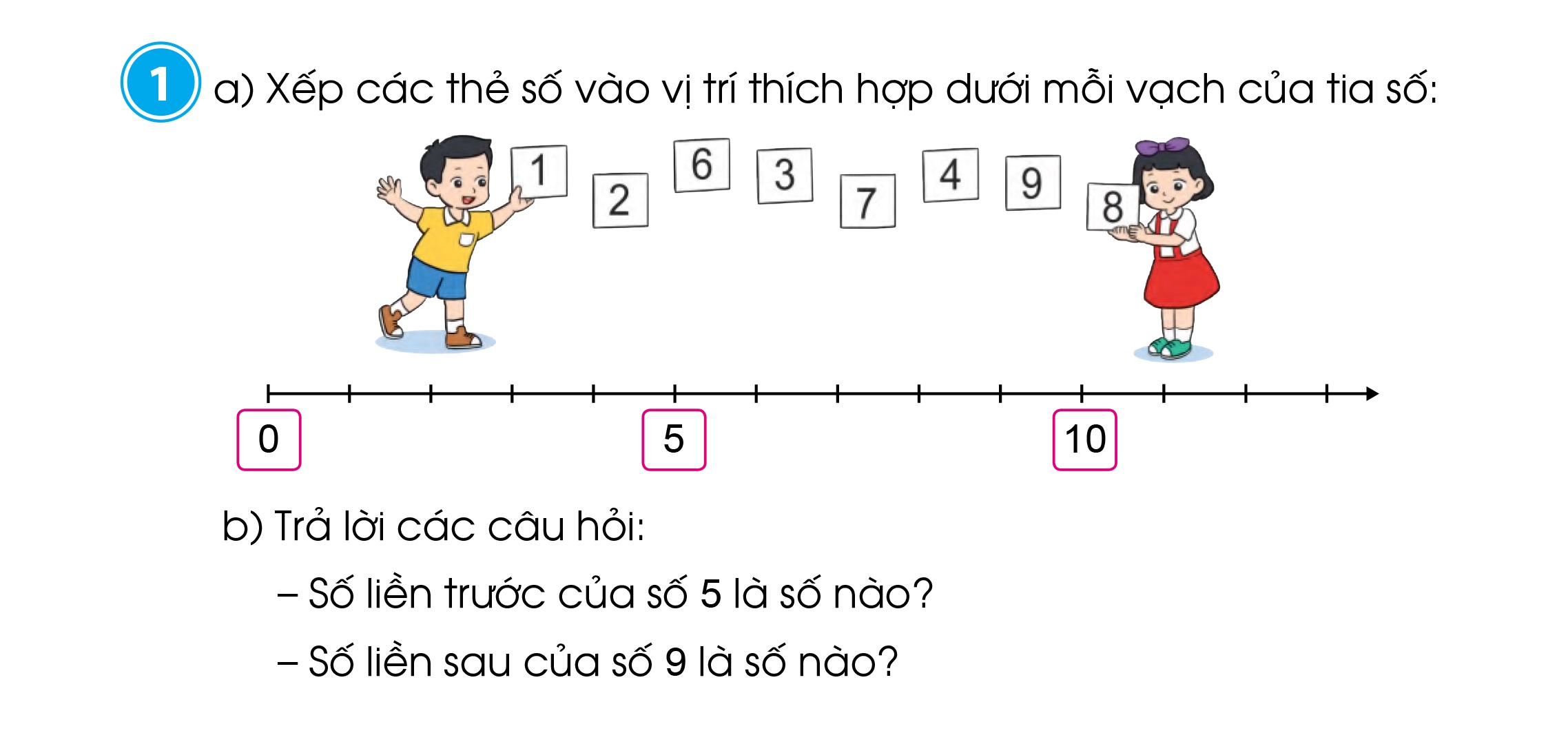
Bài tập tìm số liền trước và số liền sau của một số cho trước

Dạng bài tập này yêu cầu học sinh xác định số liền trước hoặc liền sau của một số cho sẵn. Đây là dạng bài tập cơ bản nhất để rèn luyện kỹ năng đếm số và hiểu về trật tự các số tự nhiên.

Phương pháp giải đơn giản là cộng thêm 1 đơn vị để tìm số liền sau và trừ đi 1 đơn vị để tìm số liền trước. Việc thực hành nhiều sẽ giúp học sinh hình thành phản xạ nhanh với các con số.

Bài tập điền số thích hợp vào chỗ trống

Dạng bài tập này thường xuất hiện dưới hình thức một dãy số có một số vị trí bị bỏ trống. Học sinh cần quan sát quy luật của dãy số để điền các số thích hợp vào chỗ trống.

Khi giải bài tập này, cần xác định mối quan hệ giữa các số liền kề trong dãy. Nếu là dãy số tăng dần, số sau sẽ lớn hơn số trước 1 đơn vị và ngược lại với dãy số giảm dần.

Bài tập so sánh các số liền kề nhau

Việc so sánh các số liền kề giúp học sinh hiểu sâu hơn về trật tự của các số tự nhiên. Khi so sánh hai số liền kề, số đứng sau luôn lớn hơn số đứng trước.

Để giải dạng bài tập này, học sinh cần nắm vững các dấu so sánh >, <, = và áp dụng đúng quy tắc. Việc thực hành thường xuyên sẽ giúp phát triển khả năng tư duy logic và kỹ năng tính toán nhanh.

Các bài giảng toán về chủ đề này thường được thiết kế theo hướng tăng dần độ khó, từ việc nhận biết đơn giản đến các bài tập phức hợp hơn kết hợp nhiều kỹ năng.

Mở rộng khái niệm số liền trước và số liền sau trong tập hợp số nguyên

Trong tập hợp số nguyên, số liền trước và số liền sau của một số nguyên bất kỳ được xác định bằng cách cộng hoặc trừ 1 đơn vị. Đây là một khái niệm quan trọng giúp ta hiểu được tính liên tục của dãy số nguyên.

Với mỗi số nguyên a, số liền trước của a là (a – 1) và số liền sau của a là (a + 1). Điều này áp dụng cho tất cả các số nguyên, bao gồm cả số dương, số âm và số 0. Tính chất này tạo nên một dãy số vô hạn theo hai chiều.

Khái niệm này mở rộng từ tập hợp số tự nhiên sang tập hợp số nguyên, cho phép ta xác định được số liền trước và liền sau của cả những số âm, không chỉ giới hạn ở các số dương như trong tập hợp số tự nhiên.

Số liền trước và số liền sau của số 0

Số 0 có vị trí đặc biệt trong tập hợp số nguyên khi nó đóng vai trò là điểm phân chia giữa số dương và số âm. Số liền trước và số liền sau của 0 được xác định rõ ràng theo quy tắc.

Số liền trước của 0 là -1, được tạo ra bằng cách lấy 0 trừ đi 1 đơn vị. Số liền sau của 0 là 1, được tạo ra bằng cách cộng thêm 1 đơn vị vào 0. Điều này tạo nên tính đối xứng hoàn hảo quanh điểm 0.

Số liền trước và số liền sau của các số âm

Với các số âm, việc xác định số liền trước và liền sau tuân theo quy tắc tương tự như với số dương, nhưng cần lưu ý đến dấu âm. Khi di chuyển sang phải trên trục số, giá trị tăng lên; khi di chuyển sang trái, giá trị giảm xuống.

Với một số âm a, số liền trước của nó là (a – 1), nghĩa là giảm thêm 1 đơn vị. Ví dụ, số liền trước của -3 là -4. Số liền sau của số âm a là (a + 1), nghĩa là tăng thêm 1 đơn vị. Ví dụ, số liền sau của -3 là -2.

Tính chất này giúp ta hiểu rằng dù là số âm hay dương, khoảng cách giữa hai số nguyên liên tiếp luôn là 1 đơn vị, tạo nên tính nhất quán trong toàn bộ tập hợp số nguyên.

Trong toán học, số liền trước và số liền sau là khái niệm cơ bản giúp học sinh hiểu rõ về các số tự nhiên. Qua việc xác định số liền trước và số liền sau, các bạn sẽ dễ dàng hơn trong việc so sánh và giải quyết bài tập liên quan. Việc nắm vững quy tắc tìm số này không chỉ hỗ trợ cho việc học toán mà còn giúp hình thành nền tảng vững chắc cho những kiến thức nâng cao sau này.