Hướng dẫn cách giải phương trình trùng phương và ứng dụng trong toán học

Phương trình trùng phương là dạng phương trình đặc biệt, có ứng dụng rộng rãi trong các bài toán thực tế. Bài viết cung cấp kiến thức chi tiết về khái niệm, các dạng phương trình và phương pháp giải. Qua đó, bạn sẽ nắm vững cách giải phương trình trùng phương để áp dụng hiệu quả trong học tập và thi cử.

Phương trình trùng phương là phương trình có dạng ax⁴ + bx² + c = 0

Phương trình trùng phương là một dạng phương trình bậc bốn đặc biệt, trong đó số mũ của ẩn x chỉ xuất hiện ở bậc 4 và bậc 2. Đây là một trong những phương trình quan trọng trong toán học, có mối liên hệ mật thiết với hàm trùng phương.

Khi giải quyết các bài toán thực tế, phương trình trùng phương thường xuất hiện trong các tình huống liên quan đến chuyển động, dao động, hay các hiện tượng vật lý. Ví dụ như tính toán quỹ đạo chuyển động của vật thể, hay xác định biên độ dao động của một hệ thống.

Để giải phương trình này, ta thường đặt ẩn phụ t = x², từ đó chuyển về dạng phương trình bậc hai at² + bt + c = 0. Phương pháp này giúp đơn giản hóa việc tìm nghiệm và áp dụng các công thức quen thuộc của phương trình bậc hai vào việc giải phương trình trùng phương.

Các dạng phương trình trùng phương thường gặp trong chương trình toán THPT

Trong toán đại số, dạng phương trình trùng phương là một trong những dạng toán quan trọng. Phương trình này có đặc điểm là số mũ cao nhất của ẩn là 4, và các số mũ của ẩn đều là số chẵn.

Phương trình trùng phương thường xuất hiện dưới nhiều hình thức khác nhau, từ dạng chuẩn đơn giản đến các dạng biến thể phức tạp hơn. Việc nắm vững các dạng này giúp học sinh có thể giải quyết hiệu quả các bài toán liên quan.

Dạng phương trình trùng phương chuẩn ax⁴ + bx² + c = 0

Đây là dạng cơ bản nhất của phương trình trùng phương, với a, b, c là các hệ số thực và a ≠ 0. Phương pháp giải chính là đặt ẩn phụ t = x², sau đó giải phương trình bậc hai at² + bt + c = 0.

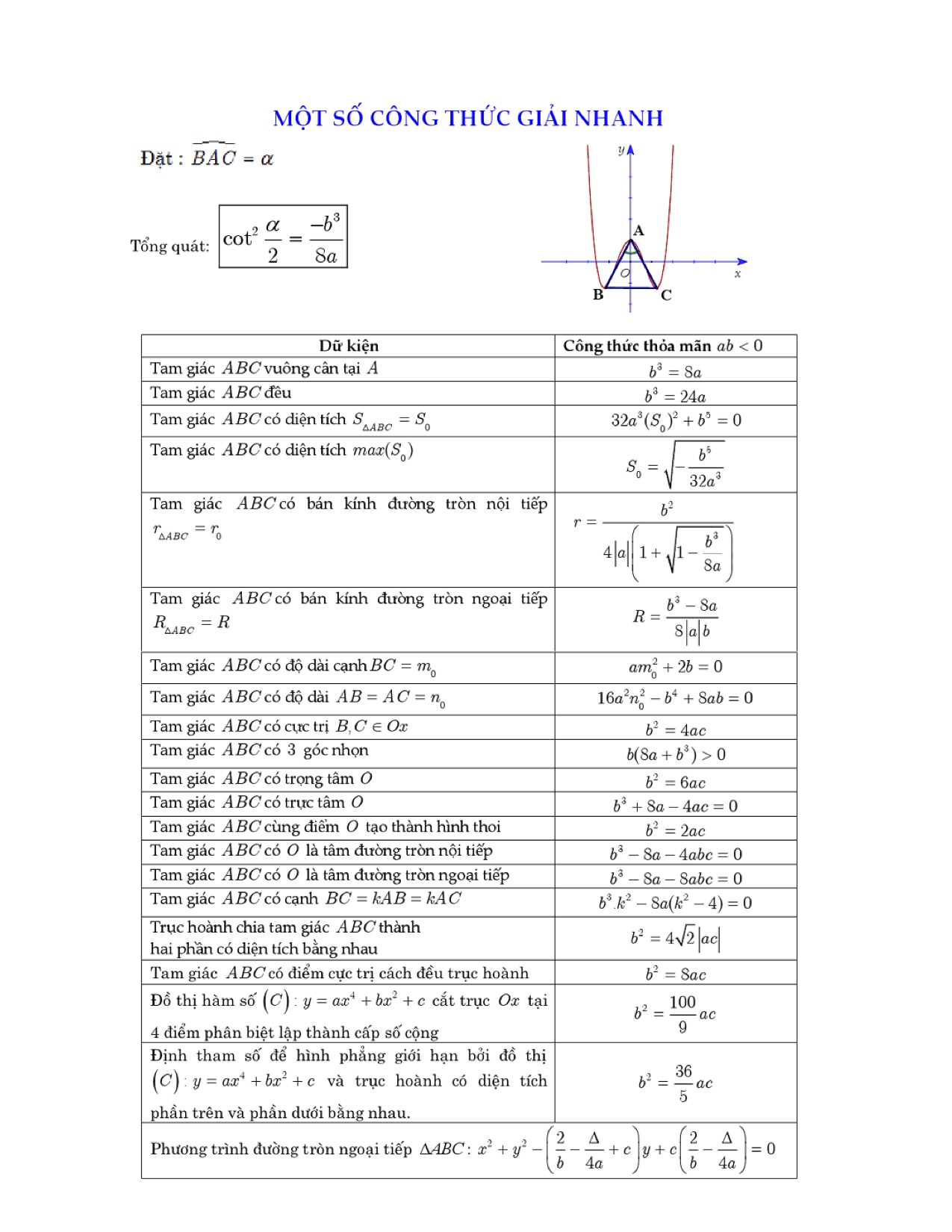
Khi có nghiệm t, ta cần xét dấu của t để tìm nghiệm x. Nếu t > 0, phương trình có hai nghiệm x = ±√t. Nếu t = 0, phương trình có nghiệm x = 0. Nếu t < 0, phương trình vô nghiệm.

Dạng phương trình trùng phương biến đổi về dạng chuẩn

Dạng này thường xuất hiện dưới dạng tích, thương hoặc tổng các đa thức. Để giải, cần thực hiện các phép biến đổi đại số để đưa về dạng chuẩn ax⁴ + bx² + c = 0.

Một số trường hợp đặc biệt có thể áp dụng phương pháp nhân cả hai vế với biểu thức chứa ẩn để khử mẫu, hoặc khai triển các nhân tử để gom các số hạng cùng bậc. Việc biến đổi cần thực hiện cẩn thận để không làm mất nghiệm hoặc xuất hiện nghiệm ngoại lai.

Dạng phương trình trùng phương chứa căn thức

Phương trình dạng này thường chứa các biểu thức căn bậc hai của các đa thức bậc hai hoặc bậc bốn. Phương pháp giải thường là bình phương hai vế để khử căn.

Khi giải phương trình có chứa căn thức, cần đặc biệt chú ý điều kiện xác định của biểu thức căn. Sau khi tìm được nghiệm, bắt buộc phải kiểm tra lại nghiệm bằng cách thế vào phương trình ban đầu để loại bỏ nghiệm không thỏa mãn điều kiện xác định hoặc nghiệm ngoại lai do bình phương hai vế.

Phương pháp giải phương trình trùng phương chi tiết từng bước

Để giải các cách giải phương trình trùng phương hiệu quả, việc nắm vững phương pháp và thực hiện theo trình tự các bước là vô cùng quan trọng. Phương trình trùng phương có dạng tổng quát ax⁴ + bx² + c = 0, trong đó a ≠ 0. Việc giải loại phương trình này đòi hỏi sự tỉ mỉ và logic trong từng bước thực hiện.

Khi giải pt trùng phương, ta cần áp dụng phương pháp đặt ẩn phụ để chuyển về dạng phương trình bậc 2 quen thuộc. Điều này giúp đơn giản hóa bài toán và tìm ra nghiệm chính xác. Tương tự như cách xác định điểm trên trục tung, việc tìm nghiệm cần được thực hiện theo trình tự rõ ràng.

Bước 1: Đưa phương trình về dạng chuẩn

Trước tiên, ta cần chuyển phương trình về dạng chuẩn ax⁴ + bx² + c = 0. Quá trình này bao gồm việc tách các số hạng chứa x⁴ và x² về một vế, số hạng tự do về vế còn lại.

Trong nhiều trường hợp, phương trình ban đầu có thể chứa các số hạng x³ hoặc x. Ta cần kiểm tra xem phương trình có thực sự là phương trình trùng phương hay không trước khi áp dụng phương pháp giải.

Bước 2: Đặt ẩn phụ và giải phương trình bậc 2

Sau khi có dạng chuẩn, ta đặt ẩn phụ t = x². Phép đặt này chuyển phương trình trùng phương thành phương trình bậc 2 với ẩn t: at² + bt + c = 0.

Tiếp theo, áp dụng công thức nghiệm của phương trình bậc 2 để tìm t₁ và t₂. Việc tính toán cần được thực hiện cẩn thận để tránh sai sót ở các bước sau.

Bước 3: Giải phương trình và kết luận nghiệm

Từ các giá trị t tìm được, ta giải các phương trình x² = t₁ và x² = t₂. Đây là bước quan trọng để xác định nghiệm cuối cùng của phương trình trùng phương ban đầu.

Cần lưu ý rằng nếu t < 0, phương trình x² = t vô nghiệm trong tập số thực. Chỉ những giá trị t ≥ 0 mới cho nghiệm thực của phương trình ban đầu. Sau khi tìm được tất cả các nghiệm, ta cần kiểm tra lại bằng cách thế vào phương trình ban đầu.

Ứng dụng của phương trình trùng phương trong thực tế và bài toán vật lý

Phương trình trùng phương xuất hiện phổ biến trong nhiều hiện tượng vật lý, đặc biệt là các bài toán liên quan đến chuyển động, điện từ trường và dao động. Các ứng dụng phương trình trùng phương giúp mô tả chính xác các quy luật tự nhiên và giải quyết nhiều vấn đề kỹ thuật quan trọng.

Trong vật lý, nhiều phương trình hiện tượng vật lý có dạng trùng phương do bản chất phi tuyến của các quá trình. Việc giải các phương trình này giúp dự đoán và kiểm soát các hiện tượng trong thực tế.

Ứng dụng trong các bài toán chuyển động

Trong lĩnh vực cơ học, phương trình trùng phương thường xuất hiện khi nghiên cứu chuyển động của vật trong trường hấp dẫn. Ví dụ như tính toán quỹ đạo của vệ tinh nhân tạo quanh Trái Đất, trong đó lực hấp dẫn tỷ lệ nghịch với bình phương khoảng cách.

Theo NASA, việc tính toán chính xác quỹ đạo của tàu vũ trụ đòi hỏi phải giải các phương trình trùng phương phức tạp, có tính đến nhiều yếu tố như lực hấp dẫn, ma sát khí quyển và ảnh hưởng của các thiên thể khác.

Ứng dụng trong các bài toán về điện từ trường

Định luật Coulomb về lực tương tác điện từ giữa các điện tích được biểu diễn bằng phương trình trùng phương. Cường độ điện trường tại một điểm tỷ lệ nghịch với bình phương khoảng cách từ điểm đó đến nguồn điện tích.

Trong thiết kế các thiết bị điện tử, kỹ sư phải giải quyết các bài toán về sự phân bố điện trường và từ trường. Công ty Intel đã ứng dụng các phương trình này để tối ưu hóa thiết kế vi xử lý, giảm thiểu nhiễu điện từ và tăng hiệu suất chip.

Ứng dụng trong các bài toán về dao động

Dao động điều hòa là một ví dụ điển hình về hiện tượng được mô tả bằng phương trình trùng phương. Phương trình dao động của con lắc đơn, dao động của lò xo hay mạch điện LC đều có dạng trùng phương.

Trong công nghiệp âm thanh, các kỹ sư sử dụng phương trình dao động để thiết kế loa và micro. Hãng Bose đã phát triển công nghệ giảm ồn chủ động dựa trên việc phân tích và điều khiển các dao động âm thanh thông qua các phương trình trùng phương.

Các nhà khoa học tại Viện Vật lý Kỹ thuật cũng ứng dụng phương trình dao động để nghiên cứu và chế tạo các cảm biến rung động, giúp cảnh báo sớm động đất và giám sát độ ổn định của các công trình xây dựng.

Bài tập và phương pháp giải các dạng phương trình trùng phương điển hình

Giải các bài tập phương trình trùng phương đòi hỏi nắm vững phương pháp và kỹ thuật giải phù hợp với từng dạng. Việc phân loại và nắm rõ các dạng bài tập sẽ giúp học sinh tiếp cận và giải quyết bài toán hiệu quả hơn.

Để giải thành công các phương trình trùng phương, học sinh cần nắm chắc cách đưa về dạng chuẩn ax⁴ + bx² + c = 0, sau đó áp dụng phương pháp đặt ẩn phụ để giải. Việc thực hành nhiều bài tập từ cơ bản đến nâng cao sẽ giúp rèn luyện kỹ năng và phát triển tư duy toán học.

Bài tập phương trình trùng phương cơ bản

Với dạng cơ bản, phương trình thường ở dạng ax⁴ + bx² + c = 0 hoặc các biến thể đơn giản. Học sinh cần nắm vững cách đặt ẩn phụ t = x², sau đó giải phương trình bậc 2 theo ẩn t và tìm x từ nghiệm của t.

Một số phương trình có thể giải nhanh bằng cách phân tích thành nhân tử. Ví dụ: x⁴ – 5x² + 4 = 0 có thể viết lại thành (x² – 1)(x² – 4) = 0, từ đó dễ dàng tìm được nghiệm x = ±1 hoặc x = ±2.

Việc thực hành nhiều bài tập cơ bản sẽ tạo nền tảng vững chắc để tiếp cận các dạng phức tạp hơn. Học sinh nên bắt đầu từ những bài tập đơn giản trước khi chuyển sang các bài khó.

Bài tập phương trình trùng phương nâng cao

Ở cấp độ nâng cao, phương trình thường xuất hiện dưới dạng phức tạp hơn, đòi hỏi kết hợp nhiều kỹ thuật giải khác nhau. Có thể là dạng phương trình chứa tham số, phương trình vô tỷ hay phương trình logarit chứa ẩn bậc 4.

Phương pháp giải thường đòi hỏi khả năng phân tích, biến đổi và áp dụng linh hoạt các công thức. Ví dụ với phương trình có tham số, cần xét các trường hợp của tham số để tìm nghiệm phù hợp.

Kỹ năng nhận dạng dạng toán và lựa chọn phương pháp giải phù hợp là yếu tố quyết định. Học sinh cần rèn luyện tư duy logic và khả năng suy luận toán học thông qua việc giải nhiều bài tập đa dạng.

Các dạng bài tập thường gặp trong đề thi

Trong các đề thi, phương trình trùng phương thường xuất hiện dưới nhiều hình thức khác nhau. Có thể là dạng kết hợp với bất phương trình, hệ phương trình hoặc các bài toán thực tế.

Một số dạng phổ biến bao gồm tìm điều kiện của tham số để phương trình có nghiệm thỏa mãn điều kiện cho trước, hoặc tìm giá trị lớn nhất, nhỏ nhất của biểu thức chứa nghiệm của phương trình.

Để đạt điểm cao trong các kỳ thi, học sinh cần luyện tập đa dạng các dạng bài tập và rèn

Phương trình trùng phương là một trong những dạng phương trình quan trọng trong toán học, có ứng dụng rộng rãi trong thực tế. Việc nắm vững phương trình trùng phương không chỉ giúp giải quyết các bài tập trong sách giáo khoa mà còn áp dụng được trong nhiều lĩnh vực như vật lý hay kỹ thuật. Tìm hiểu các dạng cũng như phương pháp giải sẽ nâng cao khả năng tư duy và kỹ năng giải quyết vấn đề của bạn.