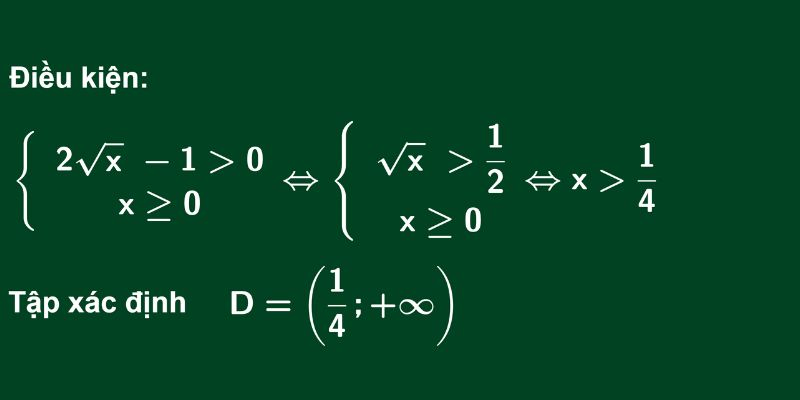Tìm hiểu tập xác định của hàm số mũ và cách xác định hiệu quả

Tập xác định của hàm số mũ đóng vai trò quan trọng trong việc xác định phạm vi giá trị của biến x. Nội dung bài viết sẽ hướng dẫn cụ thể các bước tìm tập xác định, từ đó giúp bạn hiểu rõ hơn về điều kiện và các dạng hàm số mũ khác nhau. Hãy cùng khám phá để nâng cao kiến thức toán học của mình.

Tập xác định của hàm số mũ là phạm vi giá trị của biến x để hàm số có nghĩa

Tập xác định của hàm số mũ phụ thuộc vào dạng biểu thức của hàm số. Với hàm số mũ dạng cơ bản y = ax (a > 0, a ≠ 1), tập xác định là tất cả các số thực R. Điều này cho thấy hàm số mũ luôn tồn tại và có nghĩa với mọi giá trị của biến x.

Khi xét các dạng phức tạp hơn của tập xác định hàm số mũ, ta cần chú ý đến các điều kiện ràng buộc của biểu thức. Ví dụ với hàm số y = ax+b, tập xác định vẫn là R. Tuy nhiên với dạng y = a1/x, ta cần loại trừ x = 0 khỏi tập xác định vì không thể chia cho 0.

Để hiểu rõ hơn về cách xác định tập xác định, bạn có thể tham khảo đồ thị hàm số mũ để thấy được sự biến thiên của hàm số. Việc xác định chính xác tập xác định giúp ta nắm được phạm vi hoạt động của hàm số và tránh các sai sót khi giải toán.

Một số trường hợp đặc biệt như hàm số mũ có chứa logarit hoặc căn thức sẽ có thêm các điều kiện ràng buộc. Ví dụ với y = alog(x), ta cần x > 0 để logarit có nghĩa. Việc xác định đúng các điều kiện này là bước quan trọng trong việc khảo sát hàm số.

Các dạng hàm số mũ và điều kiện xác định tập xác định tương ứng

Việc xác định điều kiện hàm số mũ là bước quan trọng để giải quyết các bài toán liên quan đến giải tích. Mỗi dạng hàm số mũ sẽ có những điều kiện xác định riêng, phụ thuộc vào số mũ và cơ số của hàm.

Hàm số mũ với số mũ là số nguyên dương

Khi số mũ là số nguyên dương, hàm số mũ có tập xác định là tất cả các số thực. Điều này là do phép tính lũy thừa với số mũ nguyên dương luôn thực hiện được, không phụ thuộc vào giá trị của cơ số. Ví dụ với hàm f(x) = x², tập xác định là R, nghĩa là x có thể nhận mọi giá trị thực.

Đặc biệt, với số mũ chẵn, đồ thị hàm số luôn nằm phía trên trục hoành và có dạng parabol. Ngược lại, với số mũ lẻ, đồ thị hàm số đi qua gốc tọa độ và có thể nhận cả giá trị âm lẫn dương.

Hàm số mũ với số mũ là số nguyên âm

Với số mũ là số nguyên âm, tập xác định của hàm số mũ không bao gồm giá trị 0 của cơ số. Điều này là do không thể thực hiện phép chia cho 0. Ví dụ với hàm f(x) = 1/x hay x⁻¹, tập xác định là R{0}.

Đồ thị của hàm số mũ với số mũ nguyên âm có dạng hyperbol, gồm hai nhánh nằm ở phần tư thứ nhất và phần tư thứ ba của hệ trục tọa độ. Các điểm trên đồ thị không bao giờ cắt trục hoành.

Hàm số mũ với số mũ không nguyên

Tập xác định của hàm số mũ không nguyên phụ thuộc vào tính chất của số mũ. Với số mũ là phân số có mẫu số chẵn, cơ số phải không âm để đảm bảo hàm số có nghĩa. Ví dụ hàm f(x) = x^(1/2) chỉ xác định khi x ≥ 0.

Khi số mũ là phân số có mẫu số lẻ, hàm số có thể nhận cả giá trị âm của cơ số. Đặc điểm này tạo nên sự đa dạng trong đồ thị của các hàm số mũ không nguyên. Điều kiện của hàm số mũ không nguyên thường phức tạp hơn so với các trường hợp số mũ nguyên.

Phương pháp tìm tập xác định của hàm số mũ qua các bước cụ thể

Để tìm tập xác định của hàm số mũ một cách chính xác và hiệu quả, ta cần thực hiện theo một quy trình có hệ thống. Việc xác định đúng tập xác định sẽ giúp ta hiểu rõ phạm vi hoạt động của hàm số và áp dụng trong các bài toán phức tạp.

Quá trình tìm tập xác định của hàm mũ đòi hỏi sự tỉ mỉ và logic. Tương tự như talet đảo, việc nắm vững các bước tìm tập xác định sẽ giúp giải quyết nhiều dạng toán khác nhau một cách hiệu quả.

Xác định dạng hàm số mũ

Bước đầu tiên là nhận diện chính xác dạng hàm số mũ đang xét. Hàm số mũ có thể xuất hiện dưới nhiều dạng khác nhau như hàm mũ cơ bản ax, hàm mũ phức tạp có chứa biểu thức, hoặc hàm mũ kết hợp với các phép toán khác.

Việc phân loại đúng dạng hàm số mũ sẽ giúp ta áp dụng đúng điều kiện xét tập xác định. Đặc biệt với những hàm số mũ phức tạp, cần tách thành các thành phần cơ bản để xét riêng từng phần.

Áp dụng điều kiện tương ứng

Sau khi xác định dạng hàm số, ta cần áp dụng các điều kiện phù hợp. Với hàm mũ có cơ số dương khác 1, tập xác định là tất cả số thực. Trường hợp cơ số âm cần xét thêm điều kiện số mũ phải là số hữu tỉ.

Đối với hàm mũ phức tạp, cần xét thêm điều kiện của các phép toán kèm theo như phép chia, phép khai căn. Mỗi điều kiện bổ sung sẽ thu hẹp tập xác định của hàm số.

Giải hệ bất phương trình

Khi có đầy đủ các điều kiện, ta tiến hành giải hệ bất phương trình để tìm txđ của hàm số mũ. Quá trình này đòi hỏi kỹ năng giải bất phương trình và logic toán học chặt chẽ.

Kết quả thu được sau khi giải hệ bất phương trình chính là giao của các khoảng thỏa mãn. Cần kiểm tra lại kết quả bằng cách thế các giá trị biên để đảm bảo tính chính xác của tập xác định.

Việc biểu diễn tập xác định dưới dạng khoảng số hoặc ký hiệu tập hợp cần tuân theo quy tắc toán học và đảm bảo tính chặt chẽ của kết quả cuối cùng.

So sánh tập xác định của hàm số mũ với các hàm số khác

Hàm số mũ có tập xác định là tất cả các số thực, điều này tạo nên sự khác biệt lớn so với các dạng hàm số khác. Đặc điểm này giúp hàm số mũ linh hoạt hơn trong việc biểu diễn các hiện tượng tăng trưởng theo cấp số nhân.

Khi so sánh với hàm số tuần hoàn là gì, hàm số mũ không có tính chất lặp lại theo chu kỳ. Thay vào đó, đồ thị của hàm số mũ luôn tăng hoặc giảm vô hạn, phụ thuộc vào cơ số của hàm.

Tập xác định của hàm số logarit

Tập xác định của hàm số logarit phụ thuộc vào cơ số và biểu thức logarit. Với cơ số dương và khác 1, biểu thức logarit phải luôn dương để hàm số có nghĩa. Điều này tạo ra một ràng buộc quan trọng khi giải các bài toán liên quan.

Trong thực tế, các ứng dụng về thang đo Richter động đất sử dụng hàm logarit cơ số 10. Ví dụ, một trận động đất độ 6 Richter mạnh gấp 10 lần so với động đất độ 5, do đặc tính của logarit.

Tập xác định của hàm số lũy thừa

Tập xác định của hàm số lũy thừa phụ thuộc vào số mũ của hàm. Với số mũ là số nguyên dương, hàm số có tập xác định là tất cả các số thực. Tuy nhiên, khi số mũ là phân số, tập xác định sẽ bị giới hạn.

Một ví dụ điển hình là hàm số căn bậc hai, một dạng đặc biệt của hàm lũy thừa với số mũ là 1/2. Trong trường hợp này, biểu thức dưới dấu căn phải không âm để hàm số có nghĩa trong tập số thực.

Điều kiện xác định của các hàm số đặc biệt

Các hàm số đặc biệt như hàm phân thức, hàm vô tỷ đều có những điều kiện xác định riêng. Mỗi dạng hàm số yêu cầu một phương pháp xét điều kiện khác nhau để xác định miền xác định chính xác.

Trong lĩnh vực tài chính, các nhà phân tích thường sử dụng kết hợp nhiều dạng hàm số để mô phỏng biến động giá cổ phiếu. Việc hiểu rõ điều kiện xác định của từng hàm số giúp họ xây dựng mô hình dự báo chính xác hơn.

Bài tập và phương pháp giải về tìm tập xác định hàm số mũ

Việc xác định chính xác tập xác định của hàm số mũ là bước quan trọng đầu tiên khi giải các bài toán liên quan đến hàm mũ. Tập xác định sẽ cho biết những giá trị nào của biến số x có thể thay vào biểu thức để hàm số có nghĩa.

Để tìm tập xác định, cần xét kỹ dạng biểu thức của hàm số và áp dụng các điều kiện hàm mũ phù hợp. Việc này đòi hỏi sự thành thạo trong việc phân tích và giải các bất phương trình.

Các dạng bài tập thường gặp

Dạng 1 là tìm tập xác định của hàm số có dạng y = a^f(x), trong đó cần chú ý đến cơ số a và hàm f(x). Với cơ số dương khác 1, tập xác định sẽ trùng với tập xác định của f(x).

Dạng 2 là xác định tập xác định của hàm số có dạng y = f(x)^g(x). Đây là dạng phức tạp hơn vì phải xét đồng thời điều kiện của cả cơ số và số mũ.

Dạng 3 liên quan đến tập xác định hàm lũy thừa có chứa căn thức hoặc logarit. Với những bài toán này, cần kết hợp điều kiện của nhiều phép toán khác nhau.

Phương pháp giải và các lưu ý quan trọng

Bước đầu tiên là xác định dạng của hàm số mũ để áp dụng điều kiện phù hợp. Với hàm có dạng y = a^x, nếu a > 0 và a ≠ 1 thì tập xác định là R.

Khi giải các bài toán phức tạp, cần phân tích thành các trường hợp riêng và giải từng trường hợp. Việc này giúp tránh bỏ sót nghiệm hoặc đưa ra nghiệm sai.

Một lưu ý quan trọng là luôn kiểm tra lại kết quả bằng cách thế một vài giá trị cụ thể vào biểu thức. Điều này giúp phát hiện sai sót trong quá trình giải.

Bài tập mẫu có lời giải chi tiết

Ví dụ: Tìm tập xác định của hàm số y = (2x-1)^(x+2)

Bước 1: Xét điều kiện của cơ số 2x-1

• Không cần điều kiện gì vì cơ số có thể âm hoặc dương

Bước 2: Xét trường hợp cơ số bằng 0

• 2x-1 = 0 ⟺ x = 1/2
• Khi x = 1/2, số mũ x+2 = 5/2 > 0
• Vậy x = 1/2 không thuộc tập xác định

Bước 3: Xét trường hợp cơ số âm

• Khi 2x-1 < 0, số mũ x+2 phải là số nguyên
• Giải hệ: 2x-1 < 0 và x+2 ∈ Z
• x < 1/2 và x ∈ Z-2

Kết luận: Tập xác định là {x ∈ R | x < 1/2 và x ∈ Z-2} ∪ {x ∈ R | x > 1/2}

Tập xác định của hàm số mũ là vấn đề quan trọng trong việc hiểu rõ cấu trúc và hành vi của các hàm này. Để tìm tập xác định của hàm số mũ, bạn cần nắm rõ các điều kiện cụ thể cho từng dạng hàm. Việc phân tích kỹ các bước tìm tập xác định sẽ giúp bạn không chỉ giải bài tập mà còn áp dụng vào thực tiễn hiệu quả hơn. Hãy khám phá sâu hơn để nâng cao kiến thức toán học của mình!