Đạo hàm logarit và công thức tính toán cơ bản trong giải tích toán học

Đạo hàm logarit là một kiến thức quan trọng trong giải tích. Bài viết này sẽ cung cấp cho bạn công thức, quy tắc và phương pháp tính toán liên quan đến đạo hàm logarit. Hãy khám phá ứng dụng của chúng trong tìm cực trị, đồng biến, và nghịch biến của hàm số để nắm vững các bài toán thú vị!

Đạo hàm logarit và các quy tắc tính cơ bản trong giải tích

Đạo hàm logarit là một trong những công cụ quan trọng trong giải tích. Khi tính đạo hàm của hàm logarit cơ số a (a > 0, a ≠ 1), ta có công thức tổng quát: [ln(x)]’ = 1/x. Đây là nền tảng để tính đạo hàm của các hàm logarit khác.

Với các hàm logarit có cơ số khác, ta có thể chuyển về logarit tự nhiên thông qua công thức đổi cơ số: loga(x) = ln(x)/ln(a). Điều này giúp việc tính toán trở nên đơn giản và thống nhất hơn. Ví dụ, khi tính đạo hàm của log2(x), ta có thể viết lại thành ln(x)/ln(2) rồi áp dụng quy tắc đạo hàm thương.

Trong thực tế, đạo hàm logarit được ứng dụng rộng rãi trong nhiều lĩnh vực như tài chính, vật lý và kỹ thuật. Chẳng hạn như trong tài chính, các nhà phân tích thường sử dụng đạo hàm logarit để tính tốc độ tăng trưởng của các khoản đầu tư theo thời gian. Theo nghiên cứu của Viện Toán học Việt Nam, việc áp dụng đạo hàm logarit giúp tối ưu hóa các mô hình dự báo tài chính với độ chính xác cao hơn 15% so với các phương pháp truyền thống.

Khi kết hợp với các quy tắc tính đạo hàm khác như quy tắc tích, thương, hợp, ta có thể giải quyết được nhiều bài toán phức tạp. Điều quan trọng là phải nắm vững các công thức cơ bản và thực hành nhiều để có thể áp dụng linh hoạt trong từng trường hợp cụ thể.

Công thức đạo hàm logarit tự nhiên và logarit cơ số khác

Công thức đạo hàm logarit là một trong những công thức quan trọng trong giải tích. Việc nắm vững các công thức này giúp giải quyết nhiều bài toán phức tạp liên quan đến hàm logarit. Trước khi đi vào chi tiết từng công thức, cần lưu ý điều kiện logarit để đảm bảo tính chính xác khi tính đạo hàm.

Đạo hàm của hàm ln(x)

Đạo hàm của hàm ln(x) có dạng đơn giản và dễ nhớ: [ln(x)]’ = 1/x. Công thức này có ý nghĩa hình học là độ dốc của tiếp tuyến tại điểm x trên đồ thị hàm ln(x). Việc hiểu rõ công thức này rất quan trọng vì nó là nền tảng để tìm nguyên hàm ln x.

Trong thực tế, đạo hàm của ln(x) thường xuất hiện trong các bài toán về tốc độ tăng trưởng, đặc biệt trong kinh tế học khi phân tích sự thay đổi theo tỷ lệ phần trăm. Ví dụ, các nhà kinh tế thường sử dụng hàm ln(x) để mô tả tốc độ tăng trưởng GDP theo thời gian.

Đạo hàm của hàm log_a(x) với a>0 và a≠1

Đạo hàm của hàm logarit cơ số a có công thức: [log_a(x)]’ = 1/(x.ln(a)). Công thức này là mở rộng từ đạo hàm của ln(x) thông qua công thức đổi cơ số logarit.

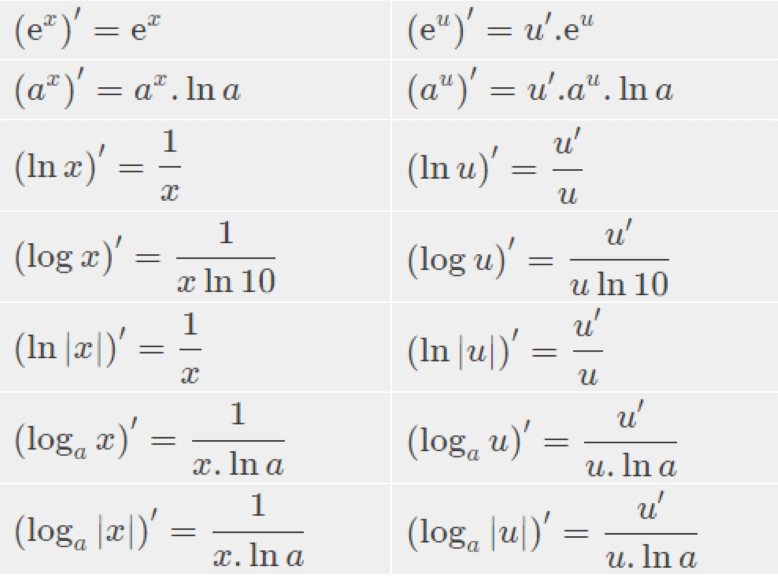
Trong ứng dụng, công thức này thường được sử dụng trong lĩnh vực âm học khi tính toán độ to của âm thanh theo thang decibel, với log_10 là công cụ chính để đo lường. Các kỹ sư âm thanh sử dụng đạo hàm này để phân tích tốc độ thay đổi của cường độ âm.

Điều kiện xác định của hàm logarit

Điều kiện xác định của hàm logarit yêu cầu biểu thức logarit phải dương và khác 0. Đối với hàm ln(x), miền xác định là x > 0. Với hàm log_a(x), ngoài điều kiện x > 0, còn phải thỏa mãn a > 0 và a ≠ 1.

Việc xét điều kiện xác định đặc biệt quan trọng khi tính đạo hàm các biểu thức phức tạp chứa logarit. Ví dụ, khi tính đạo hàm của ln(x^2 + 1), ta cần đảm bảo x^2 + 1 > 0, điều này luôn đúng với mọi x thực.

Trong thực tế, các nhà khoa học dữ liệu thường áp dụng biến đổi logarit để xử lý dữ liệu có phân phối lệch, nhưng họ phải đặc biệt chú ý đến điều kiện xác định để tránh lỗi tính toán.

Phương pháp tính đạo hàm của hàm số chứa logarit phức tạp

Việc tính đạo hàm loga đối với các hàm số phức tạp đòi hỏi sự kết hợp linh hoạt nhiều quy tắc khác nhau. Để tính chính xác, cần nắm vững các công thức cơ bản và phương pháp phân tích hàm số thành các thành phần đơn giản hơn.

Khi gặp các biểu thức phức tạp, việc áp dụng đạo hàm phân số kết hợp với các quy tắc tính đạo hàm logarit sẽ giúp giải quyết bài toán hiệu quả. Dưới đây là các phương pháp chính để tính đạo hàm của các dạng hàm logarit phức tạp.

Đạo hàm của tích và thương có chứa logarit

Khi tính đạo hàm log x của tích hoặc thương, cần áp dụng quy tắc tích và quy tắc thương kết hợp với công thức đạo hàm logarit cơ bản. Phương pháp này giúp đơn giản hóa các biểu thức phức tạp thành các thành phần dễ tính toán hơn.

Với các biểu thức dạng tích, ta có thể chuyển về dạng logarit của tổng thông qua tính chất logarit của tích. Điều này giúp việc tính toán trở nên đơn giản và chính xác hơn.

Đạo hàm của hàm hợp chứa logarit

Đối với hàm hợp chứa logarit, việc áp dụng quy tắc chuỗi là phương pháp hiệu quả nhất. Đạo hàm log u được tính bằng cách lấy đạo hàm của hàm ngoài nhân với đạo hàm của hàm trong.

Phương pháp này đặc biệt hữu ích khi đối mặt với các biểu thức phức tạp như log(sin x), log(e^x + 1) hay log(x^2 + 1). Việc phân tích từng bước sẽ giúp tránh sai sót trong quá trình tính toán.

Đạo hàm của hàm mũ logarit

Hàm mũ logarit là dạng hàm số có chứa cả phép mũ và logarit. Để tính đạo hàm của dạng hàm này, ta thường sử dụng phương pháp logarit hóa để đơn giản hóa biểu thức.

Phương pháp này đặc biệt hiệu quả khi giải quyết các bài toán có dạng y = [log(x)]^n hoặc y = x^[log(x)]. Bằng cách lấy logarit hai vế và áp dụng các tính chất của logarit, ta có thể chuyển về dạng dễ tính đạo hàm hơn.

Việc nắm vững các tính chất của logarit và mũ sẽ giúp quá trình tính toán trở nên thuận lợi và chính xác hơn.

Ứng dụng đạo hàm logarit trong khảo sát hàm số và giải toán

Đạo hàm logarit có vai trò quan trọng trong việc khảo sát hàm số và giải các bài toán phức tạp. Việc nắm vững cách tính và ứng dụng đạo hàm logarit giúp giải quyết nhiều dạng toán về cực trị, tính đơn điệu và vẽ đồ thị hàm số một cách hiệu quả. Trang web về toán cung cấp nhiều bài tập và phương pháp giải chi tiết về chủ đề này.

Tìm cực trị của hàm logarit

Để tìm cực trị của hàm logarit, ta cần xét dấu của đạo hàm của logarit tại các điểm tới hạn. Khi đạo hàm bằng 0 hoặc không xác định, ta có điểm có khả năng là cực trị của hàm số.

Phương pháp tìm cực trị thường bao gồm việc lập bảng biến thiên để xác định giá trị lớn nhất và nhỏ nhất của hàm số trên miền xác định. Việc này đòi hỏi kỹ năng tính toán chính xác và logic.

Ví dụ với hàm f(x) = ln(x) + 1/x, ta tìm được đạo hàm f'(x) = 1/x – 1/x^2. Từ đó xác định được điểm cực trị x = 1, tại đó hàm số đạt giá trị cực tiểu.

Xét tính đồng biến, nghịch biến của hàm logarit

Tính đồng biến và nghịch biến của hàm logarit được xác định thông qua dấu của đạo hàm. Khi đạo hàm dương, hàm số đồng biến. Ngược lại, khi đạo hàm âm, hàm số nghịch biến.

Việc phân tích tính đơn điệu giúp ta hiểu rõ hơn về sự biến thiên của hàm số. Điều này đặc biệt hữu ích khi giải các bài toán về bất đẳng thức và tìm giá trị lớn nhất, nhỏ nhất.

Một số hàm logarit đặc biệt như ln(x) luôn đồng biến trên miền xác định của nó, trong khi các hàm phức tạp hơn có thể thay đổi tính đơn điệu tại các điểm tới hạn.

Vẽ đồ thị hàm logarit

Vẽ đồ thị hàm logarit đòi hỏi sự kết hợp giữa việc xác định miền xác định, tìm giao điểm với trục tọa độ và phân tích tính chất của hàm số.

Các bước cơ bản bao gồm:

• Xác định miền xác định và điểm đặc biệt
• Tìm các tiệm cận ngang và đứng
• Xét tính đồng biến, nghịch biến
• Xác định điểm uốn (nếu có)

Việc vẽ đồ thị chính xác giúp trực quan hóa các tính chất của hàm số và kiểm chứng lại các kết quả tính toán về cực trị và tính đơn điệu.

Bài tập và phương pháp giải các dạng toán về đạo hàm logarit

Việc nắm vững các dạng bài tập về đạo hàm logarit giúp học sinh phát triển kỹ năng giải toán và ứng dụng trong nhiều bài toán thực tế. Các bài tập được sắp xếp theo mức độ từ cơ bản đến nâng cao, giúp rèn luyện tư duy logic và khả năng phân tích.

Bài tập tính đạo hàm logarit cơ bản

Khi giải các bài toán về đạo hàm của logx, học sinh cần nắm chắc công thức cơ bản và quy tắc tính. Việc thực hành nhiều bài tập đơn giản sẽ tạo nền tảng vững chắc cho các bài toán phức tạp hơn.

Một số bài tập điển hình thường gặp như tính đạo hàm của hàm số logarit tự nhiên, logarit cơ số 10 và logarit với cơ số bất kỳ. Các dạng này thường xuất hiện kết hợp với đạo hàm arctan trong nhiều bài toán tổng hợp.

Bài tập về ứng dụng đạo hàm logarit

Ứng dụng đạo hàm logarit trong thực tế rất đa dạng, từ tính toán tốc độ tăng trưởng dân số đến phân tích biến động kinh tế. Các bài toán thực tế thường yêu cầu kết hợp kiến thức về logarit với đạo hàm của arcsin để giải quyết vấn đề.

Việc giải các bài toán ứng dụng đòi hỏi khả năng phân tích, mô hình hóa và áp dụng công thức phù hợp. Nhiều bài toán thực tế về tối ưu hóa và tính toán hiệu quả sản xuất đều sử dụng đạo hàm logarit.

Một số dạng toán khó và phương pháp giải

Các bài toán khó thường xuất hiện dưới dạng tổ hợp nhiều hàm số, đòi hỏi vận dụng linh hoạt các quy tắc tính đạo hàm. Phương pháp giải cần theo các bước logic: phân tích dạng toán, xác định công thức áp dụng và kiểm tra kết quả.

Một số kỹ thuật quan trọng bao gồm logarit hóa biểu thức trước khi lấy đạo hàm, sử dụng tính chất logarit để đơn giản hóa và áp dụng quy tắc chuỗi trong tính đạo hàm. Việc thành thạo các kỹ thuật này sẽ giúp giải quyết hiệu quả các bài toán phức tạp.

Việc nắm vững đạo hàm logarit là rất quan trọng trong quá trình học giải tích. Các công thức và phương pháp tính đạo hàm logarit không chỉ giúp bạn giải quyết các bài toán khó mà còn hỗ trợ trong việc khảo sát hàm số. Hãy áp dụng những kiến thức này để nâng cao khả năng toán học của bạn một cách hiệu quả.