Tìm hiểu toàn diện về thể tích hình hộp tam giác và công thức tính toán hiệu quả

Thể tích hình hộp tam giác là khái niệm quan trọng trong môn hình học, giúp xác định không gian của một vật thể. Bài viết sẽ cung cấp công thức tính, hướng dẫn cách làm và các bài tập thực hành hữu ích, giúp bạn nắm vững kiến thức và áp dụng vào thực tế.

Tìm hiểu về thể tích hình hộp tam giác và các đặc điểm cơ bản

Hình hộp tam giác là gì – một khối đa diện có đáy là tam giác và các mặt bên là hình chữ nhật. Hình hộp tam giác được tạo thành bằng cách kéo dài một tam giác theo phương vuông góc với mặt phẳng chứa tam giác đó. Đây là một dạng hình học 3D phổ biến trong thực tế và ứng dụng nhiều trong kiến trúc, xây dựng.

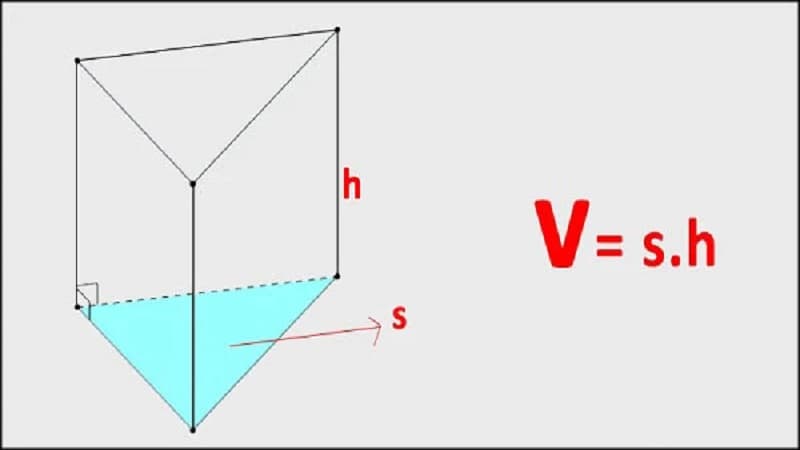
Thể tích hình hộp tam giác được tính bằng công thức: V = S.h, trong đó S là diện tích đáy (tam giác) và h là chiều cao của hình hộp. Công thức này rất đơn giản để áp dụng khi đã biết diện tích đáy và chiều cao. Ví dụ, một hình hộp tam giác có diện tích đáy 12cm2 và chiều cao 5cm sẽ có thể tích là 60cm3.

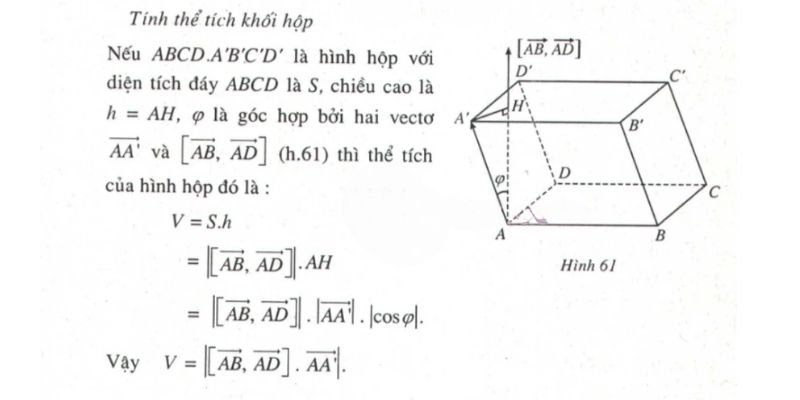
Các đặc điểm quan trọng của hình hộp tam giác bao gồm: có 5 mặt (2 mặt đáy tam giác và 3 mặt bên hình chữ nhật), 9 cạnh và 6 đỉnh. Các mặt bên luôn vuông góc với mặt đáy và song song với chiều cao của hình hộp. Đây là những tính chất cơ bản giúp phân biệt hình hộp tam giác với các khối đa diện khác.

Công thức tính thể tích hình hộp tam giác và các trường hợp đặc biệt

Hình hộp tam giác là một khối đa diện có đáy là tam giác và các mặt bên là hình chữ nhật. Để tính thể tích của khối này, cần nắm vững các công thức cơ bản và áp dụng phù hợp với từng trường hợp cụ thể. Việc tính toán chính xác công thức thể tích hình hộp tam giác giúp giải quyết nhiều bài toán thực tế trong xây dựng và thiết kế.

Công thức tổng quát tính thể tích hình hộp tam giác

Thể tích của hình hộp tam giác được tính bằng tích của diện tích đáy và chiều cao. Diện tích đáy chính là diện tích tam giác đáy, được tính theo công thức (a×h)/2, trong đó a là độ dài cạnh đáy và h là chiều cao của tam giác đáy. Khi nhân với chiều cao H của hình hộp, ta có công thức tổng quát V = (a×h×H)/2.

Trong thực tế, việc áp dụng công thức có thể linh hoạt tùy thuộc vào các yếu tố đã biết. Nếu biết ba cạnh của tam giác đáy, có thể sử dụng công thức Heron để tính diện tích đáy trước khi nhân với chiều cao hình hộp.

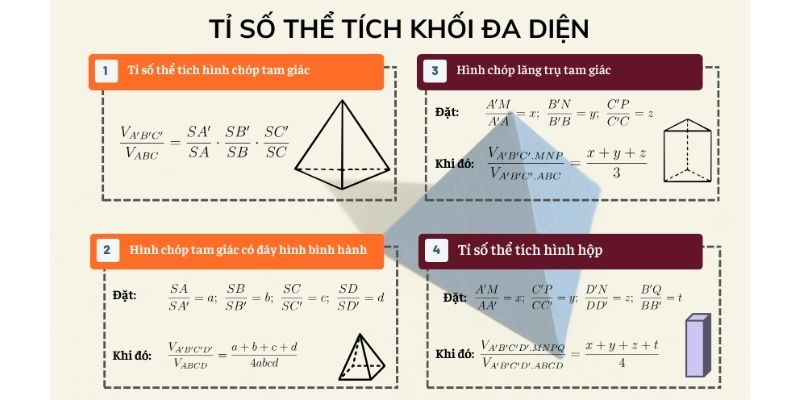
Thể tích hình hộp tam giác vuông

Thể tích hình hộp tam giác vuông có cách tính đơn giản hơn nhờ áp dụng hệ thức lượng trong tam giác vuông. Với tam giác vuông, diện tích đáy bằng tích của hai cạnh góc vuông chia 2.

Khi áp dụng vào thực tiễn, công thức này thường được sử dụng trong thiết kế mái nhà, các công trình kiến trúc có góc vuông. Ví dụ, một mái nhà có đáy là tam giác vuông với hai cạnh góc vuông 3m và 4m, chiều cao 2.5m sẽ có thể tích là (3×4×2.5)/2 = 15 mét khối.

Thể tích hình hộp tam giác đều

Thể tích hình hộp tam giác đều được tính dựa trên đặc điểm của tam giác đều – ba cạnh bằng nhau và ba góc bằng 60 độ. Diện tích đáy được tính theo công thức (a²×√3)/4, với a là độ dài cạnh tam giác đều.

Đây là trường hợp đặc biệt thường gặp trong các công trình kiến trúc mang tính thẩm mỹ cao. Ví dụ, một tháp có đáy là tam giác đều cạnh 4m và chiều cao 6m sẽ có thể tích là (16×√3×6)/4 ≈ 41.57 mét khối. Công thức này đặc biệt hữu ích trong thiết kế các công trình có tính đối xứng cao.

Hướng dẫn chi tiết cách tính thể tích hình hộp tam giác qua ví dụ

Thể tích hình hộp tam giác được xác định bằng tích của diện tích đáy và chiều cao. Để tính chính xác cách tính thể tích hình hộp tam giác, ta cần nắm vững các bước thực hiện và áp dụng công thức phù hợp với từng trường hợp cụ thể.

Việc tính thể tích hình hộp tam giác đòi hỏi sự tỉ mỉ và chính xác trong từng bước tính toán. Đặc biệt khi xác định diện tích tam giác trong oxyz, ta cần chú ý đến vị trí của tam giác đáy trong không gian ba chiều.

Các bước tính thể tích hình hộp tam giác

Bước đầu tiên là xác định tam giác đáy của hình hộp. Ta cần đo chính xác độ dài các cạnh và góc của tam giác đáy để tính diện tích chính xác.

Tiếp theo, xác định chiều cao của hình hộp tam giác bằng cách đo khoảng cách từ đỉnh đến mặt phẳng chứa tam giác đáy. Chiều cao phải vuông góc với mặt phẳng đáy.

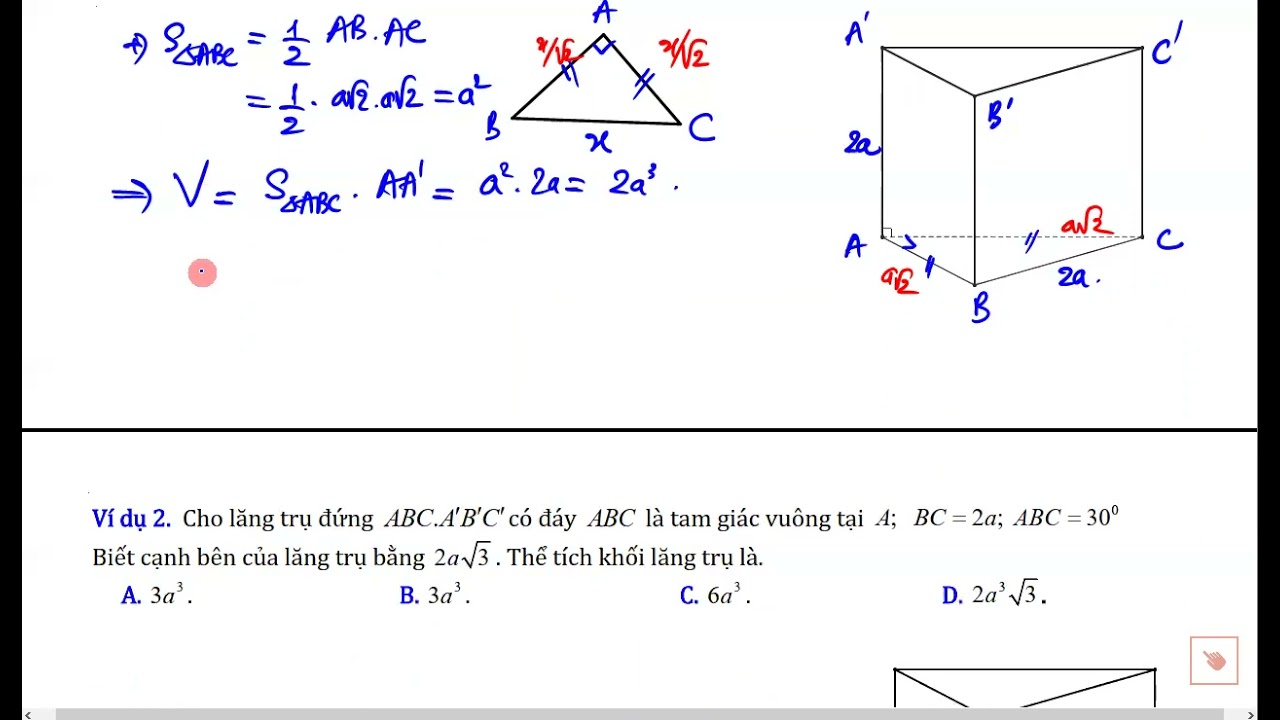
Cuối cùng, áp dụng công thức V = S.h, trong đó V là thể tích, S là diện tích tam giác đáy và h là chiều cao của hình hộp. Kết quả tính được sẽ cho ta thể tích của hình hộp tam giác.

Ví dụ minh họa và giải thích

Một ví dụ thể tích hộp tam giác điển hình: Cho tam giác đáy ABC có các cạnh lần lượt là 3cm, 4cm và 5cm, chiều cao của hình hộp là 6cm. Ta thực hiện các bước sau:

Đầu tiên tính diện tích tam giác đáy bằng công thức Heron. Với nửa chu vi p = (3 + 4 + 5)/2 = 6, ta có diện tích S = √(p(p-a)(p-b)(p-c)) = √(6(6-3)(6-4)(6-5)) = 6 cm².

Sau khi có diện tích đáy, nhân với chiều cao 6cm ta được thể tích V = 6 × 6 = 36 cm³. Kết quả này cho thấy hình hộp tam giác chiếm một thể tích khá lớn trong không gian ba chiều.

Bài tập thực hành và phương pháp giải về thể tích hình hộp tam giác

Việc nắm vững cách tính thể tích của hình hộp tam giác là kỹ năng quan trọng trong hình học không gian. Các bài tập thực hành sẽ giúp học sinh rèn luyện khả năng tư duy không gian và áp dụng công thức tính thể tích chính xác.

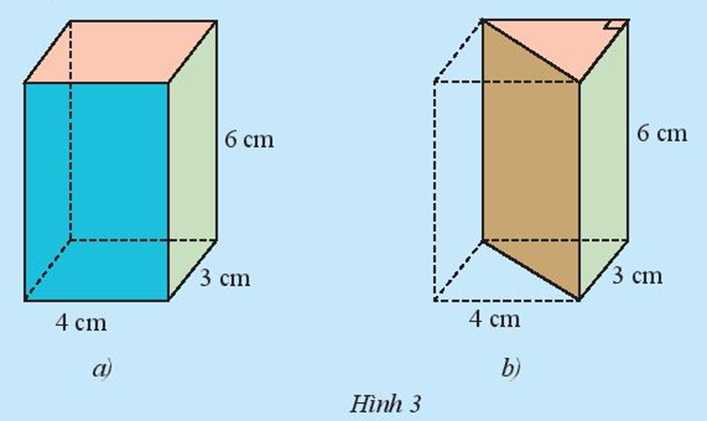
Để giải các bài tập thể tích hình hộp hiệu quả, cần nắm vững công thức cơ bản V = S.h, trong đó S là diện tích đáy và h là chiều cao. Việc xác định chính xác các yếu tố này sẽ giúp tìm ra kết quả chính xác. Tương tự như cách tính thể tích hình chóp, việc phân tích kỹ hình vẽ và các yếu tố cho trước là bước quan trọng.

Bài tập cơ bản về thể tích hình hộp tam giác

Các bài tập cơ bản thường yêu cầu tính thể tích khi biết các cạnh đáy và chiều cao của hình hộp. Đây là dạng bài tập giúp học sinh làm quen với công thức và phương pháp giải cơ bản.

Một số bài tập điển hình như tính thể tích hình hộp tam giác khi biết ba cạnh đáy và chiều cao, hoặc khi biết diện tích đáy và chiều cao. Việc giải các bài tập này giúp củng cố kiến thức nền tảng trước khi tiếp cận các dạng bài khó hơn.

Bài tập nâng cao và phương pháp giải

Ở cấp độ nâng cao, các bài tập thường kết hợp với các yếu tố phức tạp như góc, đường chéo, mặt cắt. Phương pháp giải cần vận dụng linh hoạt các kiến thức về tam giác, định lý Pytago và các công thức lượng giác.

Một số bài tập yêu cầu tìm thể tích khi biết góc giữa các mặt, hoặc khi biết đường chéo và các yếu tố khác. Việc phân tích kỹ hình vẽ, vẽ thêm các đường phụ và áp dụng các định lý hình học không gian sẽ giúp giải quyết bài toán hiệu quả.

Các bài tập về mặt cắt đòi hỏi khả năng hình dung không gian tốt, biết cách xác định giao tuyến và tính toán các yếu tố liên quan đến mặt cắt để tìm thể tích phần còn lại của hình hộp tam giác.

Ứng dụng thực tiễn của thể tích hình hộp tam giác trong cuộc sống

Ứng dụng thể tích hình hộp tam giác có vai trò quan trọng trong nhiều lĩnh vực của đời sống. Việc tính toán chính xác thể tích giúp tối ưu hóa không gian và tiết kiệm chi phí trong các công trình xây dựng cũng như sản phẩm công nghiệp.

Theo nghiên cứu của Viện Kiến trúc Quốc gia, ứng dụng thể tích hình hộp đặc biệt là dạng tam giác đã giúp tiết kiệm 15-20% chi phí vật liệu trong các công trình hiện đại. Việc áp dụng Hocthenao.vn đã giúp nhiều kiến trúc sư tối ưu hóa thiết kế và tính toán diện tích đáy hình hộp tam giác chính xác.

Ứng dụng trong kiến trúc và xây dựng

Trong lĩnh vực kiến trúc, hình hộp tam giác được ứng dụng rộng rãi để thiết kế mái nhà, tháp chuông và các công trình có kiến trúc độc đáo. Công ty kiến trúc Foster + Partners đã áp dụng nguyên lý này trong thiết kế tòa nhà The Gherkin tại London, tạo nên biểu tượng kiến trúc nổi tiếng thế giới.

Các kỹ sư xây dựng thường sử dụng tính toán thể tích hình hộp tam giác để ước lượng khối lượng vật liệu cần thiết như bê tông, thép. Điều này giúp tối ưu hóa chi phí và đảm bảo độ chính xác trong thi công.

Ngoài ra, việc áp dụng hình học tam giác trong thiết kế còn tạo ra những không gian độc đáo, tăng tính thẩm mỹ và khả năng chịu lực cho công trình.

Ứng dụng trong thiết kế và sản xuất

Trong ngành công nghiệp sản xuất, hình hộp tam giác được ứng dụng để thiết kế bao bì, container đựng hàng hóa. Theo số liệu từ Hiệp hội Bao bì Việt Nam, thiết kế bao bì dạng hình hộp tam giác giúp tiết kiệm 25% không gian lưu trữ so với bao bì truyền thống.

Các nhà sản xuất đồ nội thất cũng áp dụng nguyên lý này trong thiết kế tủ góc, kệ sách tam giác. Công ty IKEA đã phát triển nhiều sản phẩm nội thất góc sử dụng tính toán thể tích hình hộp tam giác, tối ưu hóa không gian sử dụng trong căn hộ nhỏ.

Việc ứng dụng hình học tam giác còn góp phần tạo ra những thiết kế sáng tạo, độc đáo trong các sản phẩm tiêu dùng, từ hộp đựng thực phẩm đến các thiết bị điện tử.

Trong mỗi bài toán, thể tích hình hộp tam giác đóng vai trò quan trọng trong việc tính toán và ứng dụng trong thực tế. Bài viết đã giới thiệu rõ công thức và cách tính cho các trường hợp khác nhau, cũng như ứng dụng của thể tích này trong nhiều lĩnh vực. Việc nắm vững các kiến thức về thể tích sẽ hỗ trợ học sinh và giáo viên trong việc giải bài tập hiệu quả hơn.