Lời than vãn của một nhà toán học (P1) – Paul Lockhart, Nguyễn Tiến Đạt dịch

Học Thế Nào xin được lần lượt đăng 4 phần bản dịch bài viết  “A Mathematician’s Lament” của tác giả Paul Lockhart – một nhà toán học đã giảng dạy nhiều năm tại một trường tư ở Mỹ. Bài viết bàn về cách học theo trực giác và cách giảng dạy cho phép học sinh học bằng cách chính mình tự khám phá các sự vật hiện tượng, học từ trải nghiệm của chính họ chứ không phải bằng cách nói cho họ về các sự vật hiện tượng đó. Bài viết nhấn mạnh tầm quan trọng của việc thay đổi cách giảng dạy Toán học, coi việc học Toán là một hoạt động nghệ thuật và cần nhiều trí tưởng tượng, trong khi quan điểm này chưa được thể hiện trong cách dạy Toán ở hệ thống giáo dục Mỹ.

PHẦN 1

Một nhạc công vừa choàng tỉnh dậy khỏi một cơn ác mộng kinh hoàng nhất. Trong giấc mơ, ông thấy mình mắc kẹt trong một thế giới nơi âm nhạc đã trở thành một phần bắt buộc của hệ thống giáo dục: “Chúng ta đang giúp các học sinh có thể cạnh tranh một cách tốt nhất, trong một thế giới nơi âm nhạc đang ngày càng chiếm một vị trí lớn hơn trong cuộc sống con người”, họ nói. Các nhà giáo dục, các hệ thống trường học, và cả các chính phủ đều tham gia vào dự án quan trọng này. Các nghiên cứu được triển khai, những cuộc hội thảo được tổ chức, và rất nhiều quyết định được ban bố – tất cả, hoàn toàn không có lấy sự tham vấn hay đóng góp của bất cứ một nhạc công hay một nhạc sĩ đang hoạt động nào.

Ai cũng biết các nhạc sĩ ghi lại ý tưởng của mình dưới dạng những nốt và khuông trên những bản nhạc, và do vậy, các ký tự đen trắng ngộ nghĩnh này được coi là thứ “ngôn ngữ của âm thanh”. Bởi thế, thời nay, một trong những yêu cầu bắt buộc đối với các học sinh sinh viên khi muốn lấy bất cứ một bằng cấp gì trong ngành nhạc là phải “đọc thông viết thạo” được thứ ngôn ngữ trên. Thật vậy, sẽ là quá nực cười nếu bạn tin rằng một đứa trẻ có thể hát một bài hát, hay chơi một nhạc cụ mà không cần có một chút nền tảng kiến thức nào về ký âm hay biết sơ qua các học thuyết về nhạc lý. Không nói đến sáng tác, chỉ nghe và chơi nhạc thôi cũng đã là những hoạt động được coi là có độ khó rất cao rồi, và do vậy, chỉ được dạy trong các chương trình từ mức đại học trở lên, thường phải là cao học.

Đó là về đại học, còn về các cấp học thấp hơn như tiểu học, trung học; ở đó nhiệm vụ chính của nhà giáo dục chỉ là tập trung huấn luyện để học sinh có thể sử dụng thuần thục được thứ ngôn ngữ trên, có thể sắp xếp qua lại vị trí các ký tự dựa trên các quy luật đã được soạn sẵn: “Đến giờ học nhạc, bọn em sẽ lấy giấy ký âm ra; khi giáo viên viết các nốt trên bảng, bọn em sẽ chép lại hoặc chuyển chúng về một khóa nhạc khác trên giấy. Quan trọng nhất là biểu tượng khóa nhạc và hình dáng các nốt phải chính xác; và cô giáo luôn yêu cầu bọn em rất kỹ rằng phải viết kín cho bằng hết tờ in khuông nhạc mới được. Một lần chữa bài tập về gam nửa cung, em đã trả lời đúng nhưng không được cô cho điểm, chỉ vì em đánh cái móc cho các nốt nhạc quay nhầm bên.”

Dần dần, các nhà giáo dục học thông thái nhận ra rằng, ngay cả các học sinh rất nhỏ cũng có thể được giao những dạng bài tập như trên. Và trên thực tế, vào thời buổi này, sẽ rất đáng xấu hổ cho thầy cô và các bậc cha mẹ nếu con em, học trò của họ học đến lớp 3 rồi mà vẫn chưa nắm vững được lý thuyết về các khóa và tông trong luật ký âm. “Chắc tôi phải kiếm gia sư nhạc cho thằng con tôi quá. Nó chẳng bao giờ chịu làm bài tập cả, nói những bài tập đó “chán òm”. Suốt cả ngày, lúc nào cũng chỉ thấy nó ngồi nhìn ra ngoài cửa sổ, ngâm nga một giai điệu khỉ gió gì đấy một mình, có những lúc nó còn tự bịa ra một bài hát linh ta linh tinh nào đấy nữa.”

Càng học lên cao, áp lực sẽ càng lớn; suy cho cùng, các học sinh cũng cần phải được chuẩn bị để đối mặt với các kỳ thi tiêu chuẩn sắp tới, trong đó có cả bài thi đầu vào đại học, cao đẳng. Các môn học bắt buộc trong giáo trình giảng dạy thường bao gồm: Thang âm và Gam; Điệu thứ; Nhịp Phách; Kỹ thuật hòa âm, Lý thuyết đối âm học… “Đúng là các em phải học một số lượng môn học khá lớn, tuy vậy đó là một sự chuẩn bị cần thiết; tôi tin là khi học lên các giáo trình cao hơn trong bậc đại học, yêu cầu phải trực tiếp nghe và chơi nhạc, các em sẽ thấy biết ơn tất cả những gì mình đã được học trong chương trình phổ thông…” Tất nhiên, không mấy học sinh tiếp tục đi theo con đường âm nhạc; nên sẽ chỉ có một số rất ít các em được thực sự nghe những âm thanh mà những nốt đen đen ngộ nghĩnh các em vẫn được học ký hiệu cho. Tuy vậy, điều tối quan trọng vẫn là mỗi thành viên trong xã hội đều phải có khả năng đọc được một quãng chuyển tông hay nhận ra một nhịp thứ trong các bản ký âm, bất kể là họ có bao giờ được thực sự nghe một bản nhạc hay không. “Nói thật với anh, phần lớn học sinh ngày nay không giỏi nhạc một chút nào hết. Chúng uể oải trong giờ học, kỹ thuật của chúng kém cỏi, và bài tập chép của chúng thì tệ đến mức gần như không đọc được nữa. Chẳng mấy đứa ý thức được tầm quan trọng của âm nhạc vào thời buổi hiện nay, tất cả chúng chỉ muốn làm quấy quá cho xong nhiệm vụ, miễn cứ kiếm đủ điểm tối thiểu để được lên lớp là xong. Tôi nghĩ đứa nào giỏi thì đã giỏi từ bé, còn những đứa đã bẩm sinh không có thiên khiếu thì có học thế chứ học nữa cũng vậy thôi. Mà, tôi biết có một cô bé giỏi lắm nhé, trời ơi, bài ký âm của nó, bài nào cũng phải nói là chuẩn cực luôn – mọi nốt đều ở đúng vị trí, mọi nét ký đều chính xác, sắc nét, rõ ràng, tất cả đều đẹp đến hoàn hảo! Chắc chắn rồi đây con bé sẽ trở thành một nhạc công vĩ đại cho mà xem!”

Choàng tỉnh dậy trong mồ hôi lạnh vì sợ hãi, người nhạc công nhận ra rằng, may mắn thay, tất cả đó chỉ là một giấc mơ – một cơn ác mộng điên rồ! “Tất nhiên rồi!”, ông tự trấn an bản thân, “làm gì có xã hội nào độc ác đến mức bóp chết một trong những hình thái nghệ thuật đẹp và ý nghĩa nhất của con người thành một thứ ngớ ngẩn và vô nghĩa lý đến thế! Không một nền văn hóa nào lại có thể tàn nhẫn đến độ tước đoạt đi của trẻ em một phương cách tự nhiên nhất, tuyệt vời nhất để thăng hoa, để thỏa mãn và thể hiện cảm xúc của bản thân như vậy! Thật lố bịch, quá sức lố bịch!”

Cùng lúc ấy, cách đó vài con phố, người họa sĩ của thị trấn cũng vừa choàng tỉnh khỏi một giấc mộng kinh hoàng tương tự…

Tôi kinh ngạc nhận ra mình đang ở trong một căn phòng học hoàn toàn bình thường – không giá vẽ, không ống mực, không có một thứ gì dùng để vẽ. “Ồ, ở đây chúng tôi không thực sự vẽ, cái đó phải đợi đến khi các em học đến cấp III kia” – một giáo viên trả lời thắc mắc của tôi. “Ở lớp bảy, chủ yếu các em học về màu vẽ và bảng pha màu”. Rồi họ đưa tôi xem một tờ phiếu bài tập của học sinh. Trên mặt giấy là những ô màu, bên dưới là những dòng trống, và các học sinh được yêu cầu điền vào đó tên của màu sắc trong những ô tương ứng bên trên. “Em thích môn Mỹ thuật lắm”, một học sinh hào hứng, “chỉ cần làm theo hướng dẫn là xong. Dễ nhất luôn!”.

Sau giờ học, tôi tìm đến nói chuyện với giảng viên. “Vậy các học sinh của anh không được thực sự vẽ gì hay sao?”, tôi hỏi. “Có chứ, sang năm các em sẽ được học lớp Dự bị bộ môn Vẽ-theo-số. Nó sẽ chuẩn bị cho các em kiến thức nền tảng để theo học các phân môn Vẽ-theo-số cao hơn trong bậc phổ thông. Sau đó, khi vào đời, các em sẽ có khả năng áp dụng những kiến thức được học bây giờ vào thực tế – nhúng cọ vào sơn, quét màu, lau khô, mấy thứ đại loại thế. Tất nhiên chúng tôi cũng theo dõi rất sát sao năng lực của học sinh. Những họa sĩ giỏi nhất – những em nắm vững nhất kiến thức về cọ vẽ, màu vẽ, giá vẽ – sẽ được thực sự vẽ sớm hơn, tất nhiên; nhiều em thậm chí đã có thể tự tin đăng ký lớp Dự Bị Đại Học để tích lũy tín chỉ cho đại học ngay từ bây giờ. Nhưng chủ yếu chúng tôi chỉ cố giúp các em có một hiểu biết căn bản nhất về hội họa, để sau này khi ra ngoài đời, nhỡ có lúc phải sơn lại căn bếp hay quét vôi lại mảng tường trước nhà, các em cũng không đến mức phải bỡ ngỡ.”

“Ừm, các lớp học ở phổ thông mà anh nhắc đến lúc nãy, nó là…”

“Ý anh là các lớp Vẽ-theo-số? Gần đây số lượng học sinh đăng ký học những môn đó đang tăng đột biến đấy nhé. Tôi nghĩ chúng chủ yếu đến từ các bậc cha mẹ muốn đảm bảo cho con mình sẽ vào được một trường đại học tốt. Không có gì đảm bảo cho các thí sinh tương lai tốt hơn một chứng chỉ loại giỏi môn Vẽ-theo-số trong học bạ đâu!”

“Sao các trường đại học lại đi quan tâm đến việc thí sinh của mình có biết tô màu vào đúng ô hay không?

“Ừ thì, anh biết đấy, nó cho thấy là thí sinh có một tư duy logic… vả lại nếu các em muốn được học những chuyên ngành về mỹ thuật như thiết kế thời trang hay trang trí nội thất; chẳng phải sẽ tốt hơn nếu ngay từ bậc phổ thông các em đã có thể đáp ứng đủ những yêu cầu cơ bản về hội họa hay sao?”

“Tôi hiểu rồi. Thế bao giờ thì các học sinh được vẽ tự do, trên một tấm toan trắng?”

“Anh nói cứ y như một ông giáo sư đã từng dạy tôi hồi xưa ấy! Lúc nào cũng rao giảng về việc hội họa là phải thể hiện bản thân, rồi thể hiện cảm xúc rồi các thứ này nọ… toàn những thứ huyễn hoặc, trừu tượng đâu đâu ấy! Tôi á, tôi cũng có một bằng đại học về hội họa đấy, nhưng chẳng mấy khi tôi làm việc với một tấm toan trắng tinh không có gì cả. Tôi chỉ hay dùng những bộ dụng cụ Vẽ-theo-số được nhà trường cấp là chủ yếu thôi.”

* * *

Đáng buồn thay, hệ thống giáo dục toán của chúng ta hiện nay đang giống chính xác như những cơn ác mộng kinh khủng trên. Trên thực tế, nếu bạn bảo tôi phải thiết kế ra một hệ thống hoàn hảo với mục đích tối thượng là hủy hoại hoàn toàn trí tò mò và tình yêu với việc tự phát hiện ra những quy luật của riêng mình ở trẻ em, tôi chắc chắn sẽ không thể làm tốt hơn những gì đang được làm hiện nay – Tôi chỉ đơn giản là không có đủ trí tưởng tượng để có thể nghĩ ra hàng đống những ý tưởng quá sức tàn nhẫn và vô nghĩa lý, như những cái đang tạo nên nền giáo dục toán học ngày nay!

Ai cũng biết là có gì đó không ổn ở đây. Các quan chức chính phủ nói “Chúng ta cần những tiêu chuẩn khắt khe hơn!”. Các nhà trường thì nói “Chúng ta cần thêm tiền và trang thiết bị hiện đại hơn!”. Các nhà giáo dục nói một kiểu, và các thầy cô lại nói một kiểu khác nữa. Và tất cả đều sai. Những người duy nhất thực sự hiểu chuyện gì đang xảy ra lại là những người luôn bị đổ lỗi nhiều nhất, và ít được lắng nghe nhất: các học sinh. Các em nói: “Giờ Toán nào cũng chán òm!”. Và các em đã nói hoàn toàn chính xác!

* * *

Toán học và văn hóa

Đầu tiên chúng ta cần phải hiểu rằng, Toán học cũng là một môn nghệ thuật. Sự khác biệt giữa toán và các loại nghệ thuật khác, như âm nhạc hay hội họa, đấy là nền văn hóa của chúng ta không nhìn nhận nó như thế. Ai cũng biết rằng các nhà thơ, họa sĩ, nhạc sĩ sáng tạo nên những tác phẩm nghệ thuật, và tự thể hiện mình qua chất liệu của ngôn ngữ, màu sắc hoặc âm thanh. Trên thực tế, xã hội còn khá là nhân nhượng với từ “sáng tạo”: đến cả những kiến trúc sư, đầu bếp, thậm chí cả đạo diễn phim truyền hình cũng có thể được coi là những “nghệ sĩ”. Vậy tại sao các nhà toán học lại không thể được thừa nhận như vậy?

Một phần của vấn đề là ở chỗ, hầu như không ai hiểu một cách thực sự các nhà toán học làm gì.  Quan niệm thường thấy nhất của số đông có vẻ là các nhà toán học, theo một cách nào đấy, làm những việc liên quan đến khoa học – có thể họ giúp các nhà khoa học nghĩ ra những công thức và thuật toán; hay nhập những con số rất lớn vào máy tính vì một lý do gì đấy. Không cần hỏi cũng biết, nếu có một ngày thế giới phải chia thành hai nhóm: nhóm “những người mơ mộng lãng mạn” và nhóm “những người tư duy lý trí”; chắc chắn hầu hết mọi người sẽ xếp các nhà toán học vào dạng thứ hai: nhóm “những người tư duy lý trí”.

Tuy vậy, thực tế không có thứ gì thơ mộng, lãng mạn; không thứ gì cấp tiến, cách mạng; cũng không thứ gì có thể khiến người ta mê đắm, ảo mị như toán học. Nó ẩn chứa nhiều những kinh ngạc và bất ngờ không hề thua kém vũ trụ học [1] hay vật lý (các nhà toán học đã mường tượng ra khái niệm hố đen từ rất lâu trước khi các nhà thiên văn thực sự tìm thấy một hố đen); và cho người ta nhiều tự do để thể hiện mình hơn thơ, họa, nhạc rất nhiều (những hình thái nghệ thuật này luôn bị phụ thuộc vào các nguyên liệu vật chất, hoặc có tính hạn định như ngôn ngữ, màu sắc, âm thanh). Toán học là hình thức nghệ thuật thuần khiết nhất, cũng là hình thức nghệ thuật bị hiểu sai nhiều nhất.

Bởi vậy xin hãy để tôi được giải thích toán học là gì, và các nhà toán học thực sự làm gì. Tôi nghĩ mình không thể làm tốt hơn lời miêu tả thực xác đáng sau đây của nhà toán học người Anh G.H. Hardy:

“Một nhà toán học, cũng như một họa sĩ hay nhà thơ, là một người tìm ra các quy luật. Nếu những quy luật của anh ta có bền vững hơn của một họa sĩ hay một nhà thơ, thì đó là vì chúng là quy luật của những ý tưởng.”

Vậy các nhà toán học ngồi một chỗ, tìm ra quy luật của những ý tưởng. Nhưng loại quy luật như thế nào? Loại ý tưởng như thế nào? Ý tưởng về loài tê giác chăng? Không, cái đó dành cho các nhà sinh vật học. Hay ý tưởng về ngôn ngữ và các nền văn hóa? Không, hầu hết không phải là vậy. Tất cả những thứ đó đều quá phức tạp so với sở thích của một người làm toán. Nếu có một thứ có thể coi là tư tưởng thẩm mỹ chung nhất cho toán học, thì đấy là: sự đơn giản chính là vẻ đẹp. Các nhà toán học ưa thích nghĩ đến những thứ đơn giản hết mức có thể, và thứ đơn giản nhất, chính là những nằm trong trí tưởng tượng của chúng ta.

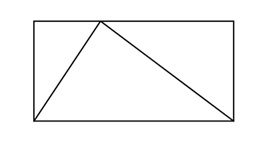
Ví dụ, nếu tôi có hứng nghĩ về các hình khối – và thường thì tôi rất hay có hứng nghĩ về chúng – tôi sẽ hình dung về một tam giác bên trong một cái hộp chữ nhật như thế này:

Tôi sẽ tự hỏi: cái tam giác kia chiếm bao nhiêu phần của cái hộp chữ nhật? Hai phần ba, có lẽ? Điều quan trọng cần nhớ ở đây là không phải tôi đang nói về cái hình vẽ trên giấy về một tam giác bên trong một hình chữ nhật. Cũng không phải tôi đang thắc mắc về một kết cấu kim loại hình tam giác trong một chi tiết dầm đỡ của một cây cầu nào đó. Hoàn toàn không có một mục đích thiết thực nào ẩn giấu trong câu hỏi này cả. Tôi chỉ đang chơi đùa vậy thôi. Đấy mới là toán – tự thắc mắc, tự chơi đùa với trí tưởng tượng của chính mình. Ngay từ đầu, cái câu hỏi “hình tam giác chiếm bao nhiêu phần của hình chữ nhật” kia đã chẳng thể áp dụng nổi với bất cứ vật thể có thực nào. Kể cả những tam giác được tạo tác một cách tinh xảo, chính xác nhất; cũng vẫn là một mớ hỗn độn quá phức tạp của hàng đống những nguyên tử và phân tử, nhảy từ bên này qua bên kia, dao động qua lại liên tục trong từng tích tắc. Đấy là, trừ khi bạn chỉ đang nói đến một hệ đo lường theo kiểu xấp xỉ. Lúc đấy thì lại là vấn đề của mỹ thuật mất rồi. Nó không hề đơn giản, và do đó, nó là một câu hỏi rất gây ức chế, bởi phụ thuộc quá nhiều vào đủ thứ chi tiết của thế giới thực. Cứ để nó cho các nhà khoa học cho xong. Câu hỏi toán học ở đây là về một tam giác tưởng tượng, bên trong một hình chữ nhật tưởng tượng. Các đường biên của chúng đều thẳng một cách tuyệt đối, bởi vì tôi muốn thế – đây mới là thứ tôi thực sự thích ở toán: mọi thứ đều có đúng những đặc tính như bạn muốn nó có. Bạn có vô hạn những lựa chọn, không hề có một thực tại nào cản trở bạn hết.

Mặt khác, một khi bạn đã quyết định các đặc tính cho đối tượng của mình (ví dụ, tôi có thể cho tam giác của mình có tính đối xứng, hoặc không); thì từ đó trở đi sáng tạo của bạn sẽ tự vận hành theo những nguyên tắc của riêng nó, bất kể bạn có muốn hay không. Đây mới là điều kỳ diệu nhất của những sáng tạo tưởng tượng này: chúng trả lời lại bạn! Có một con số đâu đó ngoài kia cho câu hỏi của tôi, nó có thể là hai phần ba, cũng có thể không, nhưng tôi không được phép quyết định nó là gì. Tôi sẽ phải tìm ra nó.

Vậy là chúng ta được thỏa sức nghĩ ra bất cứ thứ gì ta muốn, sau đó tạo ra các quy luật và đặt các câu hỏi về chúng. Nhưng làm thế nào ta có thể trả lời cho những câu hỏi kiểu này? Toán không giống như các môn khoa học: không có ống nghiệm, bình pha các kiểu để tôi có thể làm các thí nghiệm để trả lời cho câu hỏi về một thứ chỉ tồn tại trong trí tưởng tượng của tôi. Cách duy nhất để tìm ra được sự thật về một thứ tưởng tượng, đấy là phải dùng chính trí tưởng tượng, và đấy không phải là một công việc dễ dàng gì đâu.

Về trường hợp cái tam giác trong một hình chữ nhật, tôi có thấy một phương án rất đẹp và đơn giản thế này:

Nếu tôi “chém” một nhát dọc cái tam giác thế này, tôi có thể thấy rõ: mỗi nửa bị chém đều được một cạnh bên của tam giác chia đôi thành hai phần bằng nhau. Thế tức là phần không gian bên trong và phần không gian bên ngoài tam giác ở hai bên là bằng nhau. Tức là cái tam giác này chiếm đúng một nửa diện tích của hình chữ nhật!

Đây mới thực sự là một bài toán. Ví dụ ngắn vừa rồi của tôi chính là đại diện cho nghệ thuật của một nhà toán học: đặt những câu hỏi đơn giản mà sáng suốt về một đối tượng tưởng tượng của riêng mình, và tạo ra được những câu trả lời thích đáng và thỏa mãn đến tuyệt vời cho chúng. Thực sự không có gì tuyệt vời như cảm giác được tung hoành trong vương quốc của những ý tưởng: nó hấp dẫn, nó lôi cuốn người ta, và nhất là, nó hoàn toàn miễn phí!

Nhưng ý tưởng cho câu trả lời đó của tôi đến từ đâu? Sao tôi lại biết phải cần kẻ thêm đường kẻ đó? Thế tại sao một họa sĩ lại biết cần nên đặt bút vào chỗ nào trước? Cảm hứng bất chợt, kinh nghiệm, thử đi thử lại nhiều lần, ăn may. Đây chính là nét nghệ thuật của nó: tạo ra những áng tuyệt thi của suy nghĩ, những bản xô-nát của ý tưởng. Có một thứ gì đó có sức lôi cuốn, sức thay đổi rất mãnh liệt ở thứ nghệ thuật này. Mối quan hệ giữa hình tam giác và hình chữ nhật kia vốn là một điều bí ẩn, rồi xuất hiện thêm một đường kẻ, và tất cả mọi thứ bỗng đột nhiên trở nên sáng rõ. Chỉ trong phút chốc, tôi đã nhìn thấy được một điều mà lúc trước tôi không thể thấy. Bằng một cách diệu kỳ nào đó, tôi đã tạo ra được một vẻ đẹp sâu sắc chẳng từ một cái gì cả, và trong cùng lúc đó tự thay đổi chính bản thân tôi. Chẳng phải nghệ thuật chính là thế hay sao?

Đó là lý do tại sao tôi đau khổ biết bao khi nhìn những gì đang được làm với toán ở trường học. Từ một chuyến phiêu lưu đầy hấp dẫn và lôi cuốn của trí tưởng tượng, toán học đã bị rút lại thành một mớ những “định luật” để học sinh ghi nhớ và một đống các “bước”, quy trình để học sinh làm theo. Thay vì được tự mình đặt ra một câu hỏi đơn giản và tự nhiên về hai hình khối, được tự mình trải qua một quy trình tuyệt vời và đầy hưng phấn của khám phá và sáng tạo, các em học sinh lại được “chiêu đãi” một thứ như thế này đây:

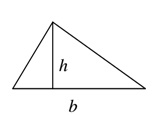
Công thức tính diện tích tam giác:

S = ½ b.h 

“Diện tích một tam giác bằng một phần hai tích của độ dài cạnh đáy và chiều cao của nó”. Học sinh được yêu cầu học thuộc công thức này, sau đó “áp dụng” lại nó, lặp đi lặp lại nhiều lần trong các “bài tập”. Còn đâu sự phấn khích, sự hứng khởi, thậm chí cả những phút khổ sở, bế tắc của quá trình sáng tạo. Ở đây thậm chí còn không có một vấn đề nào để giải quyết nữa. Câu hỏi đã được hỏi và được trả lời cùng một lúc. Chẳng còn lại gì cho các học sinh thực sự làm cả.

Hãy để tôi nói cho rõ thứ tôi đang công kích. Không phải việc các công thức, hay việc ghi nhớ những quy tắc thú vị là có gì sai trái. Trong tình huống này phải có nó ở đó, cũng giống như học ngoại ngữ thì phải nhớ từ vựng vậy – nó giúp học sinh tạo ra được những tác phẩm hay hơn, giàu có, phong phú hơn. Nhưng thứ quan trọng nhất ở đây là ý tưởng “chém” đôi cái tam giác ra bằng một đường kẻ, và việc từ một đường kẻ đó có thể dẫn ra thêm bao nhiêu ý tưởng và những đột phá mới trong sáng tạo để từ đó có thể giải quyết được những vấn đề khác – những thứ mà chỉ một dòng định lý không thể nào mang lại cho ta được.

Bằng cách bỏ đi hoàn toàn quá trình sáng tạo và chỉ để lại mỗi kết quả của quá trình sáng tạo ấy, bạn vô hình chung đã tự đảm bảo chắc chắn rằng sẽ không có ai có thể thực sự hiểu rõ vấn đề. Giống như là nói với tôi Michelangelo [2] đã tạo ra một tác phẩm điêu khắc tuyệt đẹp, nhưng lại không cho tôi được thấy tác phẩm đó hình dáng ra sao. Thế thì làm thế nào nó có thể khơi gợi cảm hứng cho tôi hay làm tôi rung động được? (và trong thực tế với môn toán, sự việc còn tệ hơn nữa kia – ít nhất trong cái ví dụ trên đây, tôi vẫn còn hiểu rằng thứ tôi đang không được thưởng thức là một tác phẩm nghệ thuật ).

Bằng cách tập trung vào câu hỏi cái gì; mà xa rời câu hỏi tại sao; toán học đã bị chúng ta rút lại chỉ còn là một cái vỏ trống rỗng. Nghệ thuật của nó không nằm trong “định lý”, nó nằm trong cách giải thích, cách lập luận. Chính sự lập luận mới cho định lý nội dung của nó, chính lập luận mới quyết định câu nói được phát biểu, và ý nghĩa thực sự của câu nói đó. Nếu bạn từ chối cho học sinh của mình tham gia vào các hoạt động này – được tìm ra vấn đề của riêng chúng, được đưa ra những suy đoán và khám phá của riêng chúng, được sai, được vò đầu bứt tai vì không tìm ra cách giải, được bỗng dưng tìm thấy cảm hứng bất ngờ, và được đưa ra những cách kiến giải và chứng cứ của riêng chúng – thì tức là bạn đã tước đi khỏi chúng toán học đích thực. Vậy nên không, tôi không phải đang than phiền về sự có mặt của công thức và định luật trong các lớp học toán. Tôi đang than phiền về sự thiếu vắng của toán học trong các lớp học toán.

(còn nữa…)

Người dịch: Nguyễn Tiến Đạt.