Công thức lượng giác đóng vai trò quan trọng trong toán học, đặc biệt là trong hình học và giải tích. Việc nắm vững các công thức này không chỉ giúp giải quyết các bài toán trong lớp học mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khoa học và kỹ thuật. Bài viết dưới đây, chúng tôi sẽ cung cấp đầy đủ mọi thông tin về nội dung này.
Công thức lượng giác là gì?
Công thức lượng giác là các phương trình toán học mô tả mối quan hệ giữa các hàm số lượng giác như sin, cos, tan, cot, sec và cosec, cũng như giữa chúng với các cạnh và góc của tam giác.

Những công thức này bao gồm các biểu thức cơ bản như sin²θ + cos²θ = 1, các công thức cộng và trừ góc như sin(A+B) = sinA.cosB + cosA.sinB, công thức nhân đôi góc, và nhiều công thức khác. Chúng đóng vai trò quan trọng trong việc giải quyết các bài toán hình học, đại số và giải tích, đồng thời có ứng dụng rộng rãi trong vật lý, kỹ thuật và các ngành khoa học khác.
Công thức lượng giác của các cung liên quan đặc biệt
Các công thức lượng giác của các cung liên quan đặc biệt là một tập hợp các ct mô tả mối quan hệ giữa các hàm lượng giác của các cung có liên hệ đặc biệt với nhau.
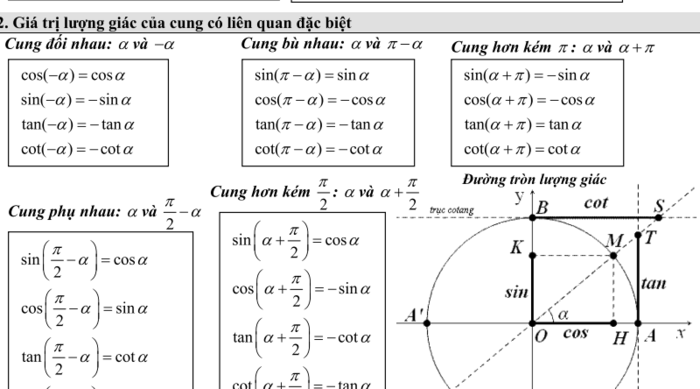
Dưới đây là các ct lượng giác chính của các cung liên quan đặc biệt:
- Cung phụ (cung có tổng π/2):
- sin(π/2 – α) = cos α
- cos(π/2 – α) = sin α
- tan(π/2 – α) = cot α
- cot(π/2 – α) = tan α
- Cung bù (cung có tổng π):
- sin(π – α) = sin α
- cos(π – α) = -cos α
- tan(π – α) = -tan α
- cot(π – α) = -cot α
- Cung đối (cung có hiệu π):
- sin(α + π) = -sin α
- cos(α + π) = -cos α
- tan(α + π) = tan α
- cot(α + π) = cot α
- Cung có tổng 2π:
- sin(α + 2π) = sin α
- cos(α + 2π) = cos α
- tan(α + 2π) = tan α
- cot(α + 2π) = cot α
- Cung đối xứng qua trục Oy:
- sin(-α) = -sin α
- cos(-α) = cos α
- tan(-α) = -tan α
- cot(-α) = -cot α
Công thức lượng giác cơ bản và nâng cao
Sau khi đã nắm rõ khái niệm về lượng giác. Các ct giác cơ bản và công thức nâng cao là những nội dung mà bạn không nên bỏ qua.
Công thức lượng giác cơ bản
Các ctlg cơ bản là nền tảng để bạn có thể tiếp cận và tìm hiểu sâu hơn về nội dung này. Các phương trình lượng giác cơ bản này được trình bày như sau:
- Ct Pytago lượng giác
- sin²α + cos²α = 1
- Các tỉ số lượng giác:
- tan α = sin α / cos α
- cot α = cos α / sin α = 1 / tan α
- sec α = 1 / cos α
- cosec α = 1 / sin α
- Các ct lượng giác cơ bản liên hệ:
- 1 + tan²α = sec²α
- 1 + cot²α = cosec²α
Các công thức phương trình lượng giác cơ bản trên là những nội dung cốt lõi mà ai cũng cần nắm rõ. Nó không chỉ có vai trò trong việc giải quyết các bài toán, mà những công thức này cũng có tính ứng dụng thực tiễn rất cao.
Công thức cộng
Công thức hàm số lượng giác cộng cho phép chúng ta tính toán các hàm lượng giác của tổng hoặc hiệu hai góc, rất hữu ích trong việc giải quyết các bài toán phức tạp. Các công thức này được trình bày như sau:
- Ct sin cộng và trừ:
- sin(α + β) = sin α cos β + cos α sin β
- sin(α – β) = sin α cos β – cos α sin β
- Ct cos cộng và trừ:
- cos(α + β) = cos α cos β – sin α sin β
- cos(α – β) = cos α cos β + sin α sin β
- Ct tan cộng và trừ:
- tan(α + β) = (tan α + tan β) / (1 – tan α tan β)
- tan(α – β) = (tan α – tan β) / (1 + tan α tan β)
Lưu ý rằng, trong công thức lượng giác 11 không hề đề cập tới cot. Mắc dù, công thức cộng cho cot thực sự tồn tại, nhưng thường không được liệt kê cùng với các công thức cộng cơ bản cho sin, cos và tan vì một số lý do:
- Phức tạp: Ct cộng cho cot phức tạp hơn so với các công thức cho sin, cos và tan.
- Ít sử dụng: Trong thực tế, công thức cộng cho cot ít được sử dụng hơn so với các phương trình khác.
- Có thể suy ra: Ct cộng cho cot có thể được suy ra từ công thức cộng của tan, vì cot là nghịch đảo của tan.
Tuy nhiên, để đáp ứng câu hỏi của bạn, tôi sẽ cung cấp công thức tính lượng giác cho cot:
- cot(α + β) = (cot α cot β – 1) / (cot α + cot β)
- cot(α – β) = (cot α cot β + 1) / (cot β – cot α)
Các công thức này có thể được suy ra từ phương trình cộng của tan bằng cách sử dụng mối quan hệ cot θ = 1 / tan θ.
Công thức nhân đôi, nhân ba và hạ bậc
Các phương trình này giúp chúng ta tính toán các hàm của góc gấp đôi, đơn giản hóa nhiều phép tính và chứng minh. Còn đối với ct hạ bậc thì cho phép chuyển đổi bình phương của hàm thành biểu thức có chứa góc kép, rất hữu ích trong việc tích phân và giải phương trình.
Phương trình lượng giác của các công thức này được trình bày như sau:
- Công thức nhân đôi:
- Sin nhân đôi: sin 2α = 2 sin α cos α
- Cos nhân đôi: cos 2α = cos²α – sin²α = 2cos²α – 1 = 1 – 2sin²α
- Tan nhân đôi: tan 2α = 2 tan α / (1 – tan²α)
- Công thức biến đổi lượng giác góc ba:
- Sin góc ba: sin 3α = 3 sin α – 4 sin³α
- Cos góc ba: cos 3α = 4 cos³α – 3 cos α
- Tan góc ba: tan 3α = (3 tan α – tan³α) / (1 – 3 tan²α)
- Ct biến đổi lượng giác hạ bậc:
- Sin bình phương: sin²α = (1 – cos 2α) / 2
- Cos bình phương: cos²α = (1 + cos 2α) / 2
Công thức biến đổi tổng thành tích
Những công thức phương trình lượng giác này giúp chuyển đổi tích của các hàm thành tổng, đóng vai trò quan trọng trong việc tính toán và đơn giản hóa biểu thức phức tạp.

Dưới đây là các ctlg biến tích thành tổng:
- sin α cos β = [sin(α + β) + sin(α – β)] / 2
- cos α sin β = [sin(α + β) – sin(α – β)] / 2
- cos α cos β = [cos(α + β) + cos(α – β)] / 2
- sin α sin β = [cos(α – β) – cos(α + β)] / 2
Công thức hàm lượng giác biến tổng thành tích được trình bày như sau:
- Tổng của sin: sin α + sin β = 2 sin((α + β)/2) cos((α – β)/2)
- Hiệu của sin: sin α – sin β = 2 cos((α + β)/2) sin((α – β)/2)
- Tổng của cos: cos α + cos β = 2 cos((α + β)/2) cos((α – β)/2)
- Hiệu của cos: cos α – cos β = -2 sin((α + β)/2) sin((α – β)/2)
Như vậy bên trên là toàn bộ những công thức lượng giác đặc biệt mà chúng tôi muốn cung cấp cho bạn. Mặc dù không được sử dụng nhiều như những công thức cơ bản, nhưng giá trị sử dụng và ứng dụng thực tiễn của các công thức này vô cùng lớn.
Lời kết
Có thể thấy, công thức lượng giác đóng vai trò then chốt trong toán học và các ngành khoa học ứng dụng. Từ công thức cơ bản đến các công thức phức tạp hơn như công thức cộng, nhân đôi, góc ba, và biến đổi tổng thành tích, chúng tạo nên một hệ thống toán học mạnh mẽ và linh hoạt.




