Công thức định lý Pythagore đảo và ứng dụng trong hình học hiệu quả

Công thức định lý pytago đảo là một phần quan trọng của hình học phẳng, giúp nhận biết và chứng minh tính chất của tam giác vuông. Bài viết này sẽ cung cấp chi tiết nội dung, chứng minh và ứng dụng thực tế của định lý trong việc giải toán. hãy cùng khám phá những bài tập thú vị và phương pháp giải hiệu quả để nâng cao kỹ năng toán học của bạn.

Công thức định lý pytago đảo và ứng dụng trong hình học phẳng

Công thức định lý pytago đảo phát biểu rằng: Trong một tam giác, nếu bình phương một cạnh bằng tổng bình phương hai cạnh còn lại thì tam giác đó là tam giác vuông. Đây là mệnh đề đảo của định lý pytago và có ý nghĩa quan trọng trong việc chứng minh một tam giác là tam giác vuông.

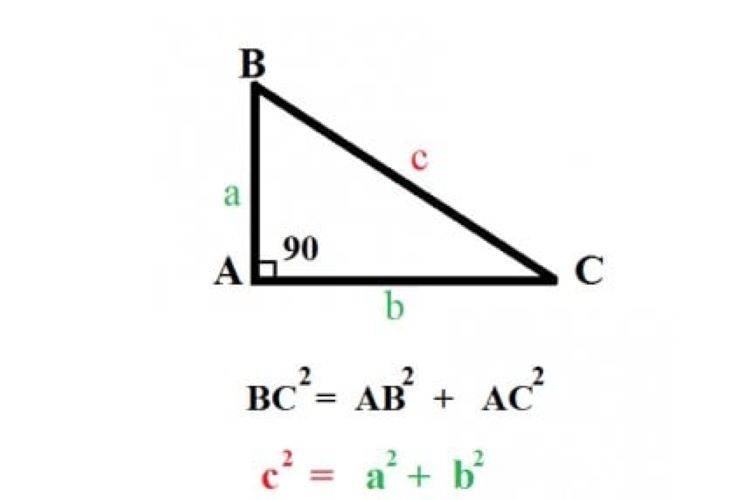
Công thức toán học của định lý được thể hiện như sau: Cho tam giác ABC có ba cạnh a, b, c. Nếu a² = b² + c² thì tam giác ABC vuông tại đỉnh đối diện với cạnh a. Tương tự, nếu b² = a² + c² thì tam giác vuông tại đỉnh đối diện với cạnh b, và nếu c² = a² + b² thì tam giác vuông tại đỉnh đối diện với cạnh c.

Trong thực tế, định lý pytago đảo thường được áp dụng để kiểm tra tính vuông góc của các cấu trúc hình học. Ví dụ, khi xây dựng nhà, người thợ có thể dùng dây đo với tỷ lệ 3-4-5 để kiểm tra góc vuông của tường. Nếu ba cạnh của tam giác có độ dài tương ứng là 3m, 4m và 5m, theo định lý pytago đảo, góc giữa cạnh 3m và 4m chắc chắn là góc vuông vì 5² = 3² + 4².

Phát biểu và chứng minh định lý Pythagore đảo trong tam giác

Định lý Pythagore đảo là một trong những định lý quan trọng trong hình học, giúp xác định một tam giác có phải là tam giác vuông hay không. Định lý này có mối liên hệ chặt chẽ với định lý Pythagore thuận và được ứng dụng rộng rãi trong thực tế. Để hiểu rõ hơn về định lý này, Hãy cùng tìm hiểu chi tiết tại Hocthenao.vn.

Nội dung định lý Pythagore đảo

Trong một tam giác ABC bất kỳ, nếu bình phương độ dài cạnh lớn nhất bằng tổng bình phương độ dài hai cạnh còn lại thì tam giác đó là tam giác vuông. Cụ thể, nếu a, b, c là độ dài ba cạnh của tam giác và c là cạnh dài nhất, khi c² = a² + b² thì tam giác đó là tam giác vuông tại đỉnh đối diện với cạnh c.

Định lý này có ý nghĩa quan trọng vì nó cung cấp điều kiện đủ để xác định một tam giác là tam giác vuông mà không cần đo góc trực tiếp. Điều này đặc biệt hữu ích trong các bài toán thực tế và trong xây dựng.

Chứng minh định lý bằng phương pháp phản chứng

Để chứng minh định lý, ta sử dụng phương pháp phản chứng với các bước logic sau:

Giả sử tam giác ABC có c² = a² + b² nhưng không phải là tam giác vuông. Khi đó, góc đối diện với cạnh c phải là góc nhọn hoặc góc tù.

Nếu góc đó là góc nhọn, theo định lý cosine: c² < a² + b² Nếu góc đó là góc tù, theo định lý cosine: c² > a² + b²

Cả hai trường hợp đều mâu thuẫn với giả thiết c² = a² + b². Do đó, giả thiết ban đầu sai, tam giác ABC phải là tam giác vuông.

Điều kiện để áp dụng định lý

Việc áp dụng định lí pytago đảo cần đảm bảo các điều kiện cơ bản sau:

Tam giác phải thỏa mãn bất đẳng thức tam giác: tổng hai cạnh bất kỳ phải lớn hơn cạnh còn lại. Điều này đảm bảo ba độ dài cho trước có thể tạo thành một tam giác.

Cần xác định chính xác cạnh dài nhất trong tam giác. Nếu áp dụng công thức với cạnh không phải là cạnh dài nhất, kết luận sẽ không chính xác.

Các phép đo cần được thực hiện chính xác để tránh sai số trong tính toán, đặc biệt khi áp dụng trong các bài toán thực tế.

Các dạng bài tập thường gặp về định lý pytago đảo

Việc nắm vững các dạng bài tập về bài tập Pythagore đảo giúp học sinh phát triển tư duy logic và kỹ năng giải toán hiệu quả. Các dạng bài tập này thường xuất hiện trong chương trình toán THCS và các kỳ thi quan trọng.

Bài tập chứng minh tam giác vuông

Để chứng minh một tam giác là tam giác vuông, ta cần kiểm tra xem bình phương cạnh lớn nhất có bằng tổng bình phương hai cạnh còn lại hay không. Phương pháp này dựa trên định lý pitago đảo và thường áp dụng cho các bài toán hình học phức tạp.

Một cách tiếp cận khác là sử dụng các yếu tố đã biết như độ dài các cạnh, các góc hoặc các yếu tố khác của tam giác để chứng minh điều kiện của định lý Pythagore đảo. Việc này đòi hỏi sự linh hoạt trong tư duy và khả năng vận dụng các kiến thức hình học đã học.

Bài tập tính độ dài cạnh tam giác

Khi biết được một tam giác là tam giác vuông và có đủ thông tin về hai cạnh, ta có thể tính được độ dài cạnh còn lại. Phương pháp này thường được áp dụng trong các bài toán thực tế như đo đạc địa hình hay xây dựng.

Việc tính toán cần tuân theo quy trình chặt chẽ: xác định cạnh huyền, hai cạnh góc vuông và áp dụng công thức phù hợp. Đặc biệt chú ý đến đơn vị đo và làm tròn số theo yêu cầu của bài toán.

Bài tập về diện tích và chu vi

Các bài toán về diện tích và chu vi thường kết hợp định lý Pythagore đảo với các công thức tính diện tích tam giác. Sau khi chứng minh được tam giác vuông, ta có thể áp dụng các công thức tính diện tích như: S = (a×h)/2 hoặc S = (a×b)/2.

Trong nhiều trường hợp, bài toán yêu cầu tìm chu vi tam giác vuông khi biết diện tích và một số yếu tố khác. Khi đó, cần kết hợp giữa công thức tính diện tích và định lý Pythagore đảo để giải quyết bài toán một cách hiệu quả.

Ngoài ra, việc nắm vững mối quan hệ giữa diện tích và chu vi trong tam giác vuông sẽ giúp giải quyết các bài toán tối ưu, như tìm diện tích lớn nhất với chu vi cho trước hoặc ngược lại.

Mối liên hệ giữa định lý Pythagore và định lý đảo

Định lý Pythagore và định lý đảo có mối liên hệ chặt chẽ, bổ trợ cho nhau trong việc chứng minh và giải các bài toán hình học. Nếu định lý Pythagore khẳng định rằng trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông, thì định lý đảo lại giúp xác định một tam giác có phải là tam giác vuông hay không dựa vào độ dài các cạnh.

Hai định lý này thường được sử dụng song song để giải quyết các bài toán phức tạp. Khi áp dụng công thức Pythagore, ta có thể tính được độ dài cạnh còn thiếu trong tam giác vuông. Ngược lại, định lý đảo giúp kiểm chứng tính chất vuông của một tam giác khi biết độ dài ba cạnh.

So sánh hai định lý

Định lý Pythagore và định lý đảo có những điểm tương đồng và khác biệt rõ rệt trong cách phát biểu và ứng dụng. Về mặt nội dung, định lý Pythagore khẳng định một điều kiện cần và đủ cho tam giác vuông, trong khi định lý đảo chỉ đưa ra điều kiện đủ.

Về phương pháp chứng minh, định lý Pythagore có nhiều cách chứng minh khác nhau như phương pháp diện tích, phương pháp đại số. Trong khi đó, định lý đảo thường được chứng minh bằng phương pháp phản chứng, sử dụng chính định lý Pythagore làm công cụ.

Trường hợp áp dụng mỗi định lý

Định lý Pythagore thường được áp dụng trong các bài toán yêu cầu tính độ dài cạnh của tam giác vuông, tính khoảng cách giữa hai điểm trong hệ tọa độ, hay giải các bài toán về hình học không gian. Định lý này đặc biệt hữu ích khi cần xác định độ dài đường chéo hình chữ nhật hoặc hình vuông.

Định lý đảo thường được sử dụng trong các bài toán đòi hỏi chứng minh một tam giác là tam giác vuông. Ví dụ, khi cần chứng minh đường thẳng kẻ từ một đỉnh vuông góc với cạnh đối diện, hay khi cần kiểm tra tính vuông góc của hai đường thẳng trong không gian.

Cả hai định lý đều có vai trò quan trọng trong việc giải quyết các bài toán thực tế như đo đạc địa hình, xây dựng công trình, hay thiết kế các sản phẩm công nghiệp đòi hỏi độ chính xác cao.

Ứng dụng định lý pytago đảo trong giải toán hình học

Định lý Pytago đảo là công cụ hữu hiệu để giải các bài toán hình học phức tạp. Công thức định lý pytago đảo giúp chứng minh một góc trong tam giác là góc vuông khi biết ba cạnh thỏa mãn điều kiện bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

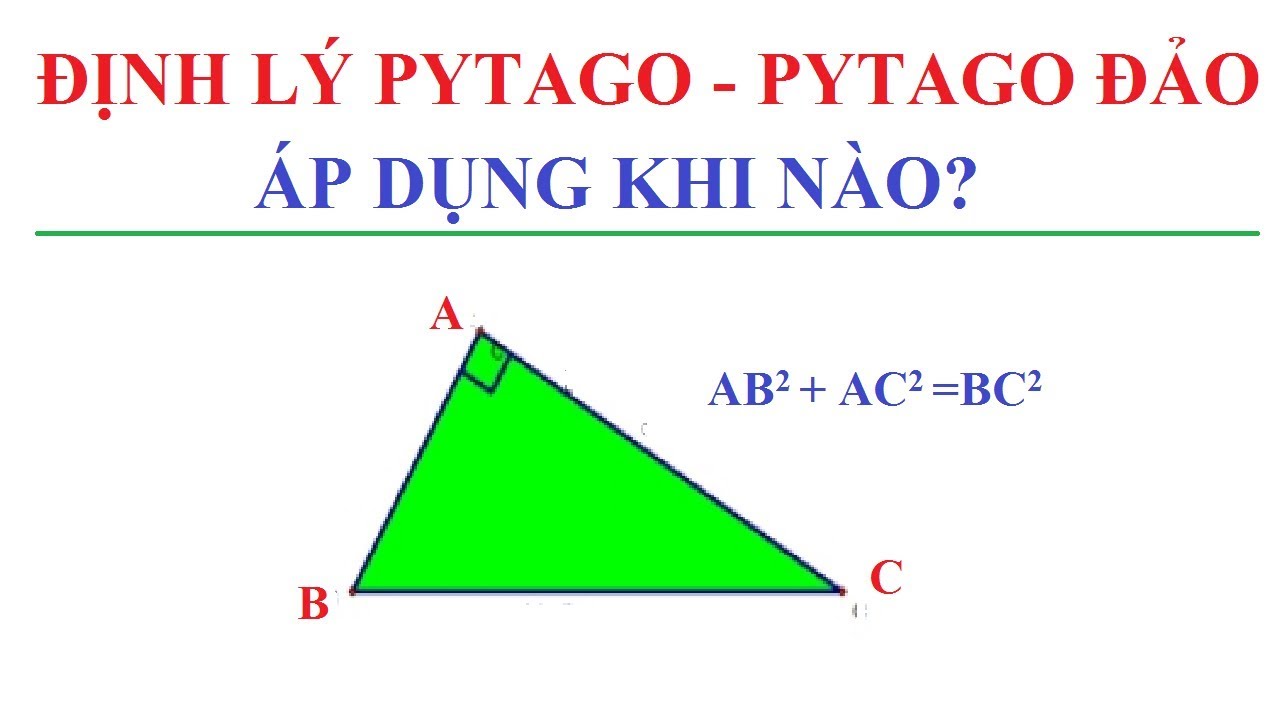
Việc áp dụng định lý này đòi hỏi sự linh hoạt và kết hợp với nhiều kiến thức khác như công thức lượng giác để giải quyết các bài toán đa dạng. Dưới đây là một số ứng dụng chính của định lý Pytago đảo.

Chứng minh góc vuông

Khi cần chứng minh một góc trong tam giác là góc vuông, ta có thể sử dụng định lý Pytago đảo bằng cách kiểm tra quan hệ giữa các cạnh. Nếu ba cạnh của tam giác thỏa mãn điều kiện a² = b² + c², trong đó a là cạnh đối diện với góc cần chứng minh, thì góc đó chắc chắn là góc vuông.

Phương pháp này đặc biệt hữu ích khi ta không thể trực tiếp đo góc hoặc sử dụng các phương pháp chứng minh khác. Việc áp dụng định lý Pytago đảo giúp đơn giản hóa quá trình chứng minh và mang lại kết quả chính xác.

Xác định tính chất tam giác

Tính chất tam giác vuông có thể được xác định thông qua mối quan hệ giữa các cạnh. Khi một tam giác có ba cạnh a, b, c thỏa mãn a² > b² + c², tam giác đó là tam giác tù. Ngược lại, nếu a² < b² + c², tam giác đó là tam giác nhọn.

Việc nắm vững các điều kiện này giúp ta nhanh chóng phân loại được tam giác mà không cần đo góc trực tiếp. Điều này đặc biệt quan trọng trong các bài toán tổng hợp yêu cầu phân tích nhiều yếu tố của tam giác.

Kết hợp với công thức lượng giác

Định lý Pytago đảo kết hợp với các công thức lượng giác tạo nên công cụ mạnh mẽ để giải quyết các bài toán phức tạp. Khi áp dụng song song cả hai kiến thức này, ta có thể tính được độ dài cạnh, số đo góc và nhiều yếu tố khác của tam giác.

Ví dụ, khi biết một góc trong tam giác là 90° thông qua định lý Pytago đảo, ta có thể sử dụng các công thức sin, cos để tìm các yếu tố còn lại. Sự kết hợp này mở rộng khả năng giải quyết các bài toán đa dạng trong hình học.

Phương pháp giải nhanh và hiệu quả các bài toán về định lý pytago đảo

Định lý Pytago đảo là một trong những công cụ quan trọng để kiểm tra tính vuông góc của tam giác. Công thức định lý pytago đảo giúp xác định nhanh chóng liệu một tam giác có vuông hay không dựa trên độ dài 3 cạnh.

Để áp dụng hiệu quả định lý này, cần nắm vững các phương pháp giải nhanh và chính xác. Giải thích định lý Pythagore một cách đơn giản: nếu bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông thì tam giác đó là tam giác vuông.

Việc sử dụng các công thức hiệu quả trong hình học sẽ giúp rút ngắn thời gian giải toán và tăng độ chính xác. Dưới đây là các bước và lưu ý quan trọng khi áp dụng định lý Pytago đảo.

Các bước giải cơ bản

Bước đầu tiên là xác định 3 cạnh của tam giác cần kiểm tra. Cần ghi nhận rõ độ dài từng cạnh và đặt tên phù hợp để tránh nhầm lẫn trong quá trình tính toán.

Tiếp theo, tìm cạnh có độ dài lớn nhất trong 3 cạnh. Cạnh này sẽ được coi là cạnh huyền tiềm năng khi kiểm tra điều kiện tam giác vuông.

Cuối cùng, áp dụng công thức kiểm tra bằng cách bình phương cạnh dài nhất và so sánh với tổng bình phương hai cạnh còn lại. Nếu hai vế bằng nhau, tam giác đó chắc chắn là tam giác vuông.

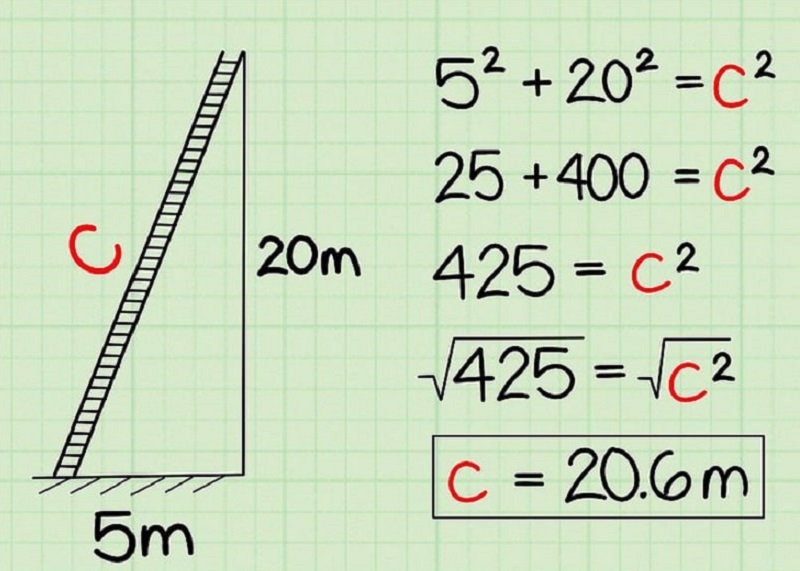
Mẹo nhận biết dạng bài

Khi gặp bài toán liên quan đến tam giác, cần chú ý các từ khóa như “kiểm tra”, “chứng minh tam giác vuông” hoặc “xác định góc vuông”. Đây thường là dấu hiệu của bài toán áp dụng định lý Pytago đảo.

Trong nhiều trường hợp, bài toán không trực tiếp yêu cầu kiểm tra tam giác vuông nhưng việc chứng minh tính vuông góc lại là bước quan trọng để giải quyết bài toán. Ví dụ như các bài toán về đường cao, đường trung tuyến hay diện tích tam giác.

Một số bài toán có thể cho các thông tin gián tiếp về độ dài các cạnh thông qua tỉ lệ hoặc biểu thức đại số. Khi đó cần chuyển đổi thành các giá trị cụ thể trước khi áp dụng định lý.

Lưu ý khi áp dụng

Việc làm tròn số trong quá trình tính toán có thể ảnh hưởng đến kết quả cuối cùng. Nên giữ nguyên dạng căn bậc hai hoặc phân số khi so sánh để đảm bảo độ chính xác.

Trong một số trường hợp đặc biệt, tam giác có thể có nhiều cặp cạnh tạo thành góc vuông. Cần kiểm tra kỹ tất cả các khả năng trước khi đưa ra kết luận cuối cùng.

Khi áp dụng định lý vào các bài toán phức tạp, nên kết hợp với các kiến thức hình học khác như tính chất đường vuông góc, định lý về góc để có cách giải tối ưu nhất.

Công thức định lý pytago đảo là một công cụ hữu ích giúp xác định tính chất tam giác vuông và có nhiều ứng dụng trong hình học. Bài viết đã trình bày rõ ràng nội dung, chứng minh cũng như các dạng bài tập liên quan để bạn có thể áp dụng hiệu quả. Việc nắm vững kiến thức này sẽ hỗ trợ bạn giải quyết các vấn đề hình học phức tạp một cách dễ dàng hơn.