Tìm hiểu định lý cosin và công thức áp dụng trong tam giác hiệu quả

Định lý cosin là một công thức quan trọng giúp tính cạnh tam giác khi biết hai cạnh cùng góc xen giữa. Qua bài viết, bạn sẽ khám phá cách phát biểu, chứng minh và áp dụng định lý này trong nhiều bài toán thực tiễn. Hãy cùng tìm hiểu sâu hơn để nắm vững kiến thức về định lý cosin nhé!

Định lý cosin là công thức tính cạnh tam giác khi biết hai cạnh và góc xen giữa

Định lý cosin là một công thức quan trọng trong hình học, mở rộng từ định lý pythagore để áp dụng cho mọi tam giác. Công thức này cho phép tính độ dài một cạnh của tam giác khi biết hai cạnh còn lại và góc xen giữa chúng.

Trong lý thuyết lượng giác, định lí cosin được xem là công cụ đắc lực để giải các bài toán tam giác. Công thức này đặc biệt hữu ích khi làm việc với tam giác không vuông, nơi định lý Pythagore không thể áp dụng trực tiếp.

Công thức này có thể được áp dụng theo hai hướng: tính cạnh khi biết hai cạnh và góc xen giữa, hoặc tính góc khi biết ba cạnh của tam giác. Điều này làm cho định lý cosin trở thành một trong những công cụ linh hoạt nhất trong việc giải các bài toán hình học tam giác.

Cách phát biểu và chứng minh định lý cosin trong tam giác

Định lý cosin trong tam giác là một công thức quan trọng trong hình học, cho phép tính độ dài cạnh hoặc số đo góc của tam giác khi biết các yếu tố còn lại. Định lý này mở rộng từ định lý Pythagore và áp dụng được cho mọi loại tam giác.

Để hiểu rõ và vận dụng định lý này một cách hiệu quả, ta cần nắm vững cách phát biểu cũng như chứng minh của nó. Việc này giúp ta thấy được mối liên hệ chặt chẽ với các kiến thức hình học khác như định lý talet và định lý Pythagore.

Phát biểu định lý cosin trong tam giác vuông và tam giác bất kỳ

Trong tam giác vuông ABC vuông tại A, định lý cosin có dạng đơn giản: c² = a² + b² – 2ab.cosC, với C là góc giữa hai cạnh a và b. Đây chính là trường hợp đặc biệt của định lý Pythagore.

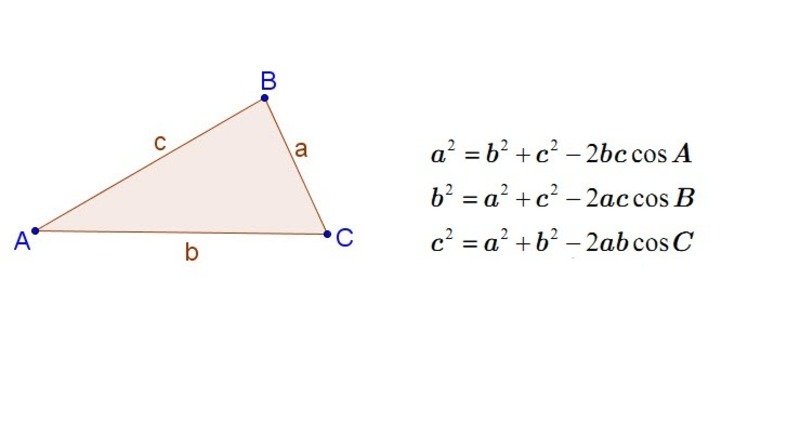
Đối với tam giác bất kỳ ABC, định lý cosin được phát biểu tổng quát hơn:

• a² = b² + c² – 2bc.cosA
• b² = a² + c² – 2ac.cosB
• c² = a² + b² – 2ab.cosC

Trong đó a, b, c là độ dài các cạnh và A, B, C là số đo các góc đối diện với các cạnh tương ứng.

Chứng minh định lý cosin bằng phương pháp hình học

Để chứng minh định lý cosin, ta xét tam giác ABC và kẻ đường cao h từ đỉnh A đến chân H thuộc cạnh BC. Gọi BH = m và HC = n.

Theo định lý Pythagore áp dụng cho tam giác AHB và AHC:
AB² = h² + BH² = h² + m²
AC² = h² + HC² = h² + n²

Từ đó suy ra: BC = m + n và h = b.sinC
Thay các giá trị và biến đổi, ta được: c² = a² + b² – 2ab.cosC

Mối liên hệ giữa định lý cosin và định lý Pythagore

Định lý cosin là sự mở rộng của định lý Pythagore. Khi tam giác có một góc vuông 90°, cosine của góc đó bằng 0, và công thức cosin trở thành định lý Pythagore quen thuộc.

Sự liên hệ này thể hiện tính kế thừa và phát triển trong toán học. Định lý Pythagore chỉ áp dụng cho tam giác vuông, trong khi định lý cos trong tam giác có thể áp dụng cho mọi loại tam giác, giúp giải quyết nhiều bài toán phức tạp hơn trong thực tế.

Việc hiểu rõ mối liên hệ này giúp ta linh hoạt trong việc lựa chọn công cụ phù hợp để giải các bài toán về tam giác, đồng thời thấy được sự phát triển logic của các định lý trong hình học.

Các dạng công thức cosin thường gặp và cách áp dụng

Công thức cosin là một trong những công thức quan trọng trong tam giác học, giúp tính toán các cạnh và góc của tam giác. Công thức này có nhiều dạng khác nhau tùy thuộc vào loại tam giác và bài toán cụ thể.

Để áp dụng hiệu quả công thức cosin, việc nắm vững các dạng cơ bản và biết cách đổi từ sin sang cos là rất quan trọng. Mỗi dạng công thức sẽ phù hợp với những tình huống khác nhau trong giải toán.

Công thức cosin cho tam giác vuông

Trong tam giác vuông, công thức cos trong tam giác được biểu diễn đơn giản nhất. Công thức này là trường hợp đặc biệt của công thức tổng quát, khi một góc của tam giác bằng 90°.

Khi áp dụng vào tam giác vuông ABC có góc C = 90°, ta có công thức: cosA = b/c, với b là cạnh kề góc A và c là cạnh huyền. Tương tự, cosB = a/c, với a là cạnh kề góc B.

Công thức cosin cho tam giác bất kỳ

Đối với tam giác bất kỳ ABC, cosin là gì được thể hiện qua công thức tổng quát: a² = b² + c² – 2bc.cosA. Công thức này áp dụng cho mọi tam giác, không phụ thuộc vào loại tam giác.

Trong thực tế, công thức này thường được sử dụng khi biết 2 cạnh và góc xen giữa, hoặc khi cần tìm một góc khi biết 3 cạnh. sinx cosx bằng gì là kiến thức bổ trợ quan trọng để giải các bài toán phức tạp hơn.

Công thức cosin trong các bài toán đặc biệt

Công thức cosin có nhiều ứng dụng đặc biệt trong các bài toán thực tế. Ví dụ trong ngành xây dựng, kỹ sư thường sử dụng công thức này để tính toán độ nghiêng của các kết cấu.

Trong lĩnh vực đo đạc địa hình, công thức cosin giúp xác định khoảng cách giữa hai điểm khi biết tọa độ của chúng. Công thức này cũng được ứng dụng trong thiết kế robot để tính toán góc quay của các khớp nối.

Ngoài ra, trong thiên văn học, các nhà khoa học sử dụng công thức cosin để tính khoảng cách giữa các thiên thể, góc nghiêng quỹ đạo và nhiều thông số quan trọng khác.

So sánh định lý cosin với các định lý lượng giác khác

Định lý cosin có mối liên hệ mật thiết với các định lý lượng giác khác trong tam giác. Việc hiểu rõ mối quan hệ này giúp giải quyết nhiều bài toán phức tạp một cách hiệu quả. Để áp dụng tốt các định lý, cần nắm vững đặc điểm và phạm vi ứng dụng của từng định lý.

Định lý cosin và định lý sin

Định lý sin và định lý cosin bổ trợ cho nhau trong việc giải tam giác. Định lý sin thường được sử dụng khi biết 2 cạnh và 1 góc đối diện hoặc 2 góc và 1 cạnh. Trong khi đó, định lý cosin phát huy hiệu quả với trường hợp biết 3 cạnh hoặc 2 cạnh và góc xen giữa.

Một điểm khác biệt quan trọng là định lý sin chỉ thiết lập tỷ lệ giữa các cạnh và sin của góc đối diện, còn định lý cosin cho phép tính trực tiếp độ dài cạnh hoặc số đo góc. Điều này khiến định lý cosin linh hoạt hơn trong nhiều tình huống thực tế.

Định lý cosin và định lý hàm số cos

Định lý hàm cos là nền tảng để chứng minh định lý cosin trong tam giác. Định lý hàm cos thiết lập mối quan hệ giữa cos của tổng/hiệu hai góc, trong khi định lý cosin mở rộng ứng dụng sang lĩnh vực hình học tam giác.

Việc kết hợp hai định lý này tạo nên công cụ mạnh mẽ để giải quyết các bài toán phức tạp về tam giác và đa giác. Như Học Thế Nào đã đề cập, sự đồng quy là gì của các phương pháp giải là chìa khóa để nâng cao hiệu quả học tập.

Ứng dụng kết hợp các định lý lượng giác

Việc phối hợp các định lý lượng giác mở ra nhiều phương pháp giải sáng tạo. Định lý hàm sin kết hợp với định lý cosin giúp giải quyết các bài toán về diện tích và thể tích hình học phức tạp.

Trong thực tế, các kỹ sư xây dựng thường áp dụng kết hợp các định lý này để tính toán kết cấu công trình. Ví dụ, khi thiết kế mái vòm, họ sử dụng định lý cosin để tính góc nghiêng của các thanh giằng, kết hợp định lý sin để xác định độ dài các cấu kiện.

Các nhà thiết kế cảnh quan cũng vận dụng sự kết hợp này để tạo ra những không gian hài hòa. Họ áp dụng các định lý lượng giác để tính toán vị trí đặt các yếu tố trang trí sao cho tạo được góc nhìn đẹp từ nhiều hướng khác nhau.

Các hệ quả và ứng dụng quan trọng của định lý cosin

Định lý cosin là một trong những công cụ toán học quan trọng giúp giải quyết nhiều bài toán phức tạp trong hình học và ứng dụng thực tế. Từ định lý này, ta có thể rút ra nhiều hệ quả và ứng dụng có giá trị.

Hệ quả về mối quan hệ giữa các cạnh và góc

Một trong những hệ quả định lý cosin quan trọng là mối liên hệ giữa độ dài các cạnh và số đo các góc trong tam giác. Khi một góc trong tam giác là góc vuông, định lý cosin sẽ trở thành định lý Pythagoras quen thuộc.

Ngoài ra, định lý này còn cho phép xác định được loại tam giác (nhọn, vuông hay tù) dựa vào độ dài các cạnh mà không cần đo góc trực tiếp. Điều này đặc biệt hữu ích trong các ứng dụng kỹ thuật khi việc đo góc gặp khó khăn.

Ứng dụng trong giải tam giác

Định lí cos được áp dụng rộng rãi trong việc giải các bài toán tam giác. Khi biết độ dài ba cạnh, ta có thể tính được số đo các góc một cách chính xác. Ngược lại, khi biết hai cạnh và góc xen giữa, ta dễ dàng tìm được cạnh còn lại.

Trong thực tế, các kỹ sư trắc địa thường sử dụng phương pháp này để đo đạc và tính toán khoảng cách giữa các điểm không thể tiếp cận trực tiếp. Ví dụ như đo chiều cao tòa nhà, độ sâu giếng khoan, hay khoảng cách giữa hai đỉnh núi.

Ứng dụng trong các bài toán thực tế

Trong lĩnh vực xây dựng, định lý cosin giúp tính toán chính xác góc nghiêng của mái nhà, độ dốc của cầu thang, hay khoảng cách giữa các điểm neo trong công trình. Theo báo cáo của Hiệp hội Kỹ sư Xây dựng, việc áp dụng định lý này giúp tiết kiệm tới 15% chi phí thiết kế và thi công.

Trong ngành hàng không, các kỹ sư sử dụng định lý cosin để tính toán quỹ đạo bay tối ưu, góc cất cánh và hạ cánh an toàn. NASA cũng áp dụng định lý này trong việc tính toán quỹ đạo của các vệ tinh và tàu vũ trụ.

Trong thể thao, huấn luyện viên bóng đá sử dụng định lý cosin để phân tích góc sút bóng hiệu quả nhất, giúp cầu thủ tăng tỷ lệ ghi bàn thành công.

Kết luận của bài viết này đã làm rõ định lý cosin và tầm quan trọng của nó trong việc tính toán các cạnh và góc của tam giác. Việc nắm vững định lý này, cùng với các công thức liên quan, giúp người học dễ dàng giải quyết các bài toán từ đơn giản đến phức tạp. Hơn nữa, những ứng dụng thực tiễn của định lý cosin mang lại cái nhìn sâu sắc về sự kết nối giữa toán học và cuộc sống hàng ngày.