Điều kiện phương trình mặt cầu và bài toán hình học không gian cơ bản

Điều kiện phương trình mặt cầu rất quan trọng để xác định tính chính xác trong hình học không gian. Bài viết này khám phá các yếu tố cơ bản, từ dạng tổng quát đến các điều kiện cần có để nhận diện mặt cầu. Những kiến thức này cùng với bài tập cụ thể sẽ giúp bạn nắm vững phương pháp và ứng dụng mặt cầu trong toán học.

Điều kiện phương trình mặt cầu và các yếu tố cơ bản để xác định

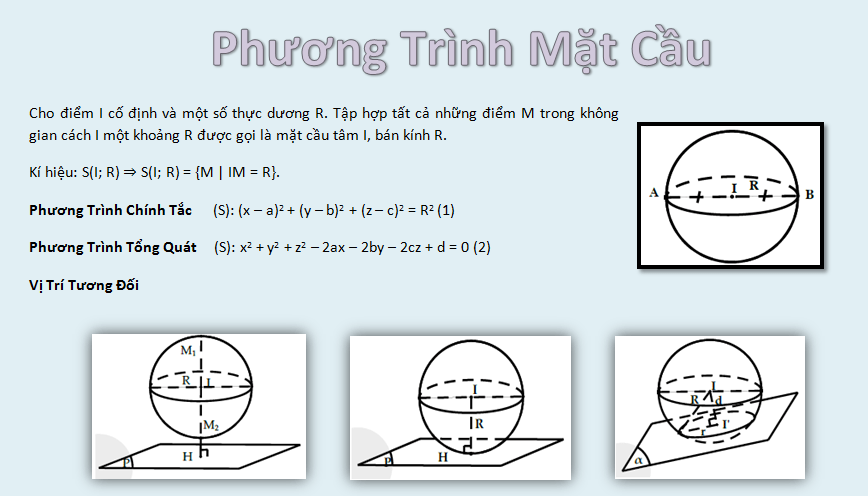
Điều kiện phương trình mặt cầu cần thỏa mãn dạng tổng quát (x – a)² + (y – b)² + (z – c)² = R², trong đó (a,b,c) là tọa độ tâm và R là bán kính. Khi khai triển, phương trình sẽ có dạng x² + y² + z² + Dx + Ey + Fz + G = 0 với D, E, F, G là các hệ số.

Hình mặt cầu được xác định hoàn toàn khi biết tâm và bán kính. Để tìm tâm từ phương trình tổng quát, ta cần đưa về dạng chính tắc bằng cách hoàn chỉnh bình phương các số hạng chứa x, y, z. Bán kính sẽ được tính từ các hệ số sau khi biến đổi.

Phương trình mặt cầu có dạng chuẩn khi các hệ số của x², y², z² bằng 1 và không có số hạng chứa tích xy, yz, zx. Điều này giúp phân biệt mặt cầu với các mặt bậc hai khác trong không gian. Nếu phương trình không thỏa mãn các điều kiện này, ta cần kiểm tra kỹ để xác định đúng dạng mặt.

Khi xét tính chất hình học, mặt cầu là tập hợp các điểm cách đều tâm một khoảng bằng bán kính. Điều này tạo nên tính đối xứng hoàn hảo của mặt cầu qua mọi mặt phẳng đi qua tâm và mọi trục đi qua tâm. Đây là đặc trưng quan trọng giúp nhận biết và phân tích các bài toán liên quan đến mặt cầu.

Dạng tổng quát và cách xác định tâm, bán kính của mặt cầu trong không gian

Phương trình mặt cầu là một dạng phương trình bậc hai đặc biệt trong không gian Oxyz. Để giải quyết các bài toán liên quan đến điều kiện pt mặt cầu, ta cần nắm vững các dạng phương trình cơ bản. Học toán sẽ giúp bạn hiểu rõ hơn về cách xác định các yếu tố của mặt cầu trong không gian.

Phương trình mặt cầu dạng chuẩn tắc

Phương trình mặt cầu dạng chuẩn tắc có tâm I(a,b,c) và bán kính R được viết dưới dạng:
(x-a)² + (y-b)² + (z-c)² = R²

Đây là dạng phương trình thể hiện khoảng cách từ một điểm bất kỳ M(x,y,z) trên mặt cầu đến tâm I luôn bằng bán kính R. Dạng này thường được sử dụng khi đã biết tọa độ tâm và bán kính của mặt cầu.

Phương trình mặt cầu dạng khai triển

Khi khai triển dạng chuẩn tắc, ta được phương trình tổng quát:
x² + y² + z² + Ax + By + Cz + D = 0

Trong đó A, B, C, D là các hệ số thực. Dạng này thường xuất hiện trong các bài toán thực tế và cần được chuyển về dạng chuẩn tắc để xác định tâm và bán kính.

Việc chuyển đổi giữa hai dạng phương trình giúp ta linh hoạt trong việc giải quyết các bài toán hình học không gian.

Cách xác định tọa độ tâm và bán kính

Để xác định tọa độ tâm và bán kính từ phương trình dạng khai triển, ta thực hiện:

Hoàn chỉnh bình phương:

• Nhóm các số hạng chứa x: x² + Ax = (x + A/2)² – A²/4
• Nhóm các số hạng chứa y: y² + By = (y + B/2)² – B²/4
• Nhóm các số hạng chứa z: z² + Cz = (z + C/2)² – C²/4

Tọa độ tâm I sẽ là:
I(-A/2, -B/2, -C/2)

Bán kính R được tính theo công thức:
R² = (A² + B² + C² – 4D)/4

Phương pháp này giúp chuyển đổi nhanh chóng giữa hai dạng phương trình và xác định chính xác các yếu tố của mặt cầu.

Các điều kiện cần và đủ để một phương trình biểu diễn mặt cầu

Một phương trình tổng quát dạng ax² + ay² + az² + 2bx + 2cy + 2dz + e = 0 sẽ biểu diễn điều kiện phương trình mặt cầu khi thỏa mãn đồng thời các điều kiện về hệ số, biệt số và bán kính. Việc xác định các điều kiện để là phương trình mặt cầu giúp phân biệt được phương trình mặt cầu với các phương trình mặt bậc hai khác trong không gian.

Điều kiện về hệ số

Hệ số của các số hạng bậc hai trong phương trình phải bằng nhau và khác 0. Điều này có nghĩa là các hệ số a của x², y², z² phải có giá trị giống nhau và không được bằng 0. Tương tự như cách xác định điều kiện của log, việc kiểm tra hệ số là bước đầu tiên và quan trọng nhất.

Nếu các hệ số không thỏa mãn điều kiện này, phương trình có thể biểu diễn các mặt bậc hai khác như mặt elipsoid, hyperboloid hoặc paraboloid. Việc kiểm tra hệ số giúp loại trừ ngay các trường hợp không phải mặt cầu.

Điều kiện về biệt số

Biệt số của phương trình mặt cầu được tính theo công thức Δ = b² + c² + d² – ae. Giá trị của biệt số phải lớn hơn 0 để phương trình có nghiệm thực. Điều này đảm bảo mặt cầu tồn tại trong không gian thực.

Khi biệt số bằng 0, phương trình sẽ biểu diễn một điểm. Trường hợp biệt số âm, phương trình không có nghiệm thực và không biểu diễn mặt cầu nào trong không gian ba chiều.

Điều kiện về bán kính

Bán kính của mặt cầu được tính theo công thức R = √(Δ/a²), trong đó a là hệ số của các số hạng bậc hai và Δ là biệt số. Giá trị bán kính phải là số thực dương để mặt cầu có thể tồn tại.

Bán kính là thông số quyết định kích thước của mặt cầu. Nếu bán kính bằng 0, mặt cầu suy biến thành một điểm. Trường hợp bán kính là số ảo hoặc âm, phương trình không biểu diễn mặt cầu trong không gian thực.

Phương pháp kiểm tra và xác định điều kiện mặt cầu

Việc xác định điều kiện để có phương trình mặt cầu đóng vai trò quan trọng trong hình học không gian. Phương trình mặt cầu có dạng tổng quát (x – a)² + (y – b)² + (z – c)² = R², trong đó (a,b,c) là tọa độ tâm và R là bán kính.

Khi triển khai phương trình, ta cần kiểm tra biểu thức có nghĩa khi nào để đảm bảo phương trình biểu diễn một mặt cầu thực sự. Việc xác định điều kiện mặt cầu giúp phân biệt với các mặt cong khác trong không gian.

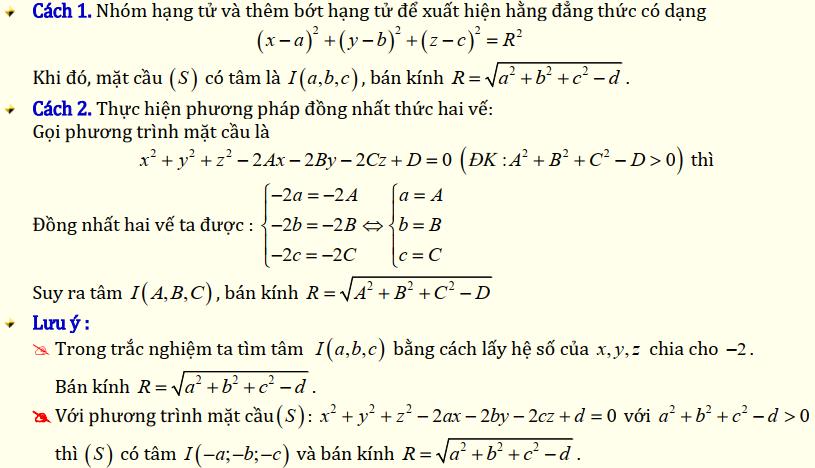
Các bước kiểm tra phương trình mặt cầu

Bước đầu tiên là đưa phương trình về dạng tổng quát bằng cách khai triển và thu gọn các số hạng. Các hệ số của x², y², z² phải bằng nhau và khác 0 để đảm bảo tính đối xứng của mặt cầu.

Tiếp theo, ta tính tọa độ tâm bằng cách hoàn chỉnh bình phương các biến. Điều kiện cần là các biểu thức trong căn phải không âm để tồn tại bán kính thực.

Cuối cùng, kiểm tra vế phải của phương trình – đây chính là bình phương bán kính. Giá trị này phải dương để mặt cầu có thể tồn tại trong không gian thực.

Ví dụ minh họa cụ thể

Xét phương trình: x² + y² + z² – 2x + 4y – 6z + 9 = 0
Khai triển và thu gọn: (x² – 2x) + (y² + 4y) + (z² – 6z) = -9
Hoàn chỉnh bình phương: (x – 1)² + (y + 2)² + (z – 3)² = 1

Qua phép biến đổi, ta xác định được:

• Tâm mặt cầu có tọa độ (1, -2, 3)
• Bán kính R = 1 > 0

Do đó phương trình trên thỏa mãn điều kiện và biểu diễn một mặt cầu trong không gian ba chiều.

Ứng dụng và bài tập về điều kiện phương trình mặt cầu

Điều kiện phương trình mặt cầu là yếu tố quan trọng giúp xác định tính chất hình học của mặt cầu trong không gian. Việc nắm vững các điều kiện và ứng dụng sẽ giúp giải quyết nhiều bài toán phức tạp liên quan đến mặt cầu và các đối tượng hình học khác.

Khi nghiên cứu về phương trình tọa độ, ta cần chú ý đến các yếu tố như tâm, bán kính và mối quan hệ với các đối tượng hình học khác. Những kiến thức này có ứng dụng rộng rãi trong thiết kế kiến trúc, công nghệ vệ tinh và nhiều lĩnh vực kỹ thuật khác.

Bài tập về xác định điều kiện

Để xác định điều kiện của mặt cầu, cần phân tích kỹ các thành phần trong phương trình. Một phương trình mặt cầu tổng quát có dạng (x-a)² + (y-b)² + (z-c)² = R², trong đó (a,b,c) là tọa độ tâm và R là bán kính.

Việc kiểm tra tính hợp lệ của các hệ số trong phương trình là bước quan trọng. Nếu R² < 0, mặt cầu không tồn tại trong thực tế. Nếu R² = 0, mặt cầu suy biến thành một điểm.

Các tính chất mặt cầu như tính đối xứng và tính liên tục cũng cần được xem xét kỹ lưỡng khi giải quyết bài toán điều kiện.

Bài tập về mối quan hệ giữa mặt cầu và mặt phẳng

Mặt cầu và mặt phẳng có thể có ba dạng quan hệ chính: cắt nhau theo đường tròn, tiếp xúc tại một điểm, hoặc không có điểm chung. Việc xác định quan hệ này phụ thuộc vào khoảng cách từ tâm mặt cầu đến mặt phẳng.

Khi giải các bài toán về giao tuyến, cần sử dụng công thức tính khoảng cách từ tâm mặt cầu đến mặt phẳng và so sánh với bán kính mặt cầu. Điều này giúp xác định chính xác dạng giao của hai đối tượng.

Trong thực tế, mối quan hệ này được ứng dụng trong thiết kế các công trình kiến trúc hình cầu, như nhà vòm hay các công trình thể thao.

Phương pháp giải các dạng bài tập điển hình

Phương pháp giải bài tập về mặt cầu thường bao gồm các bước cơ bản sau:

• Xác định các yếu tố đã cho trong đề bài
• Thiết lập phương trình mặt cầu dựa trên các điều kiện
• Kiểm tra tính hợp lý của nghiệm

Ứng dụng mặt cầu trong thực tế rất đa dạng, từ thiết kế kiến trúc đến công nghệ vệ tinh. Ví dụ, trong thiết kế nhà vòm Olympic Montreal, các kỹ sư đã sử dụng tính chất của mặt cầu để tạo ra kết cấu vững chắc và thẩm mỹ.

Việc nắm vững phương pháp giải sẽ giúp giải quyết hiệu quả các bài toán từ cơ bản đến nâng cao về mặt cầu trong không gian ba chiều.

Việc nắm rõ điều kiện phương trình mặt cầu là yếu tố quan trọng giúp bạn xác định và ứng dụng tính chất của mặt cầu trong không gian. Bài viết đã cung cấp những kiến thức cơ bản về yếu tố cấu thành phương trình, điều kiện cần thiết, cũng như các phương pháp kiểm tra. Hiểu biết này không chỉ giúp bạn giải quyết bài tập mà còn phát triển tư duy hình học trong toán học.