Hình chữ nhật có bao nhiêu trục đối xứng? Ứng dụng trục đối xứng của hình chữ nhật trong thực thế như thế nào? Tất cả sẽ được chúng tôi giải đáp cụ thể, chi tiết ngay trong bài viết dưới đây.
Định nghĩa về trục đối xứng
Trục đối xứng của một hình bất kỳ là đường thẳng mà khi gấp hình theo đường thẳng đó, hai nửa của hình sẽ khớp nhau hoàn toàn. Như vậy, với đặc điểm và tính chất của hình chữ nhật thì loại hình này sẽ có hai trục chính.
Trục đối xứng của hình chữ nhật là gì?
Trục đối xứng của hình chữ nhật là các đường thẳng chia hình thành hai phần bằng nhau. Đó là đường thẳng đi qua trung điểm của hai cạnh đối diện.
Để hiểu hơn về trục đối xứng của hình chữ nhật, bạn cần phân biệt sự khác nhau giữa trung điểm và trục, cụ thể như sau:
- Trục đối xứng: Là đường thẳng chia tách HCN thành hai nửa bằng nhau, mỗi phần là ảnh phản chiếu của phần kia. Một hình chữ nhật bao giờ cũng chỉ có 2 trục.
- Trung điểm: Là điểm chính giữa của một cạnh hình chữ nhật. Hcn có bốn trung điểm, mỗi trung điểm nằm ở giữa một cạnh.
Tóm lại, trục đối xứng là đường thẳng chia đôi HCN, còn trung điểm là điểm giữa của một cạnh.
Xem thêm: Hình chữ nhật là gì? Tính chất, định nghĩa và bài tập ứng dụng
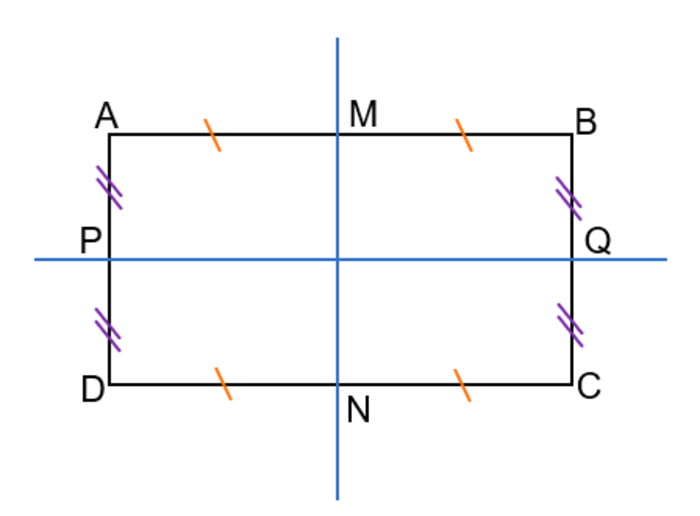
Hình chữ nhật có mấy trục đối xứng?
Hình chữ nhật có 2 trục đối xứng. Các trục này đi qua trung điểm của hai cạnh đối diện. Cụ thể:
- Trục đối xứng thứ nhất: Đây là trục đối xứng chia hcn thành hai nửa trên và dưới. Trục này đi qua trung điểm của hai cạnh ngắn của hình chữ nhật và song song với cạnh dài.
- Trục đối xứng thứ hai: Đây là trục đối xứng chia hình chữ nhật thành hai nửa trái và phải. Trục này đi qua trung điểm của hai cạnh dài của hcn và song song với cạnh ngắn.
Cụ thể hơn, khi xét một hình chữ nhật có chiều dài là a và chiều rộng là b:
- Trục đối xứng thứ nhất sẽ là đường thẳng nằm ngang tại y=b/2.
- Trục đối xứng thứ hai sẽ là đường thẳng đứng tại x=a/2.
Vì hình chữ nhật có hai cặp cạnh đối song song và bằng nhau, nên nó chỉ có hai trục đối xứng này. Các đường chéo của hcn không phải là trục đối xứng, vì chúng không chia hình chữ nhật thành hai phần gương đối xứng nhau.
Tìm hiểu thêm: Tính chất hình chữ nhật có 2 đường chéo vuông góc
Ví dụ trực quan về trục đối xứng của hình chữ nhật
Để hiểu rõ hơn về trục đối xứng trong hình chữ nhật, chúng ta có thể xem các ví dụ sau:
- Ví dụ 1: Xét một hình chữ nhật ABCD, với AB và CD là hai cạnh dài, BC và AD là hai cạnh ngắn. Trục đối xứng thứ nhất đi qua trung điểm của BC và AD, song song với các cạnh dài (AB và CD).
- Ví dụ 2: Đường thẳng đi qua trung điểm của AB và CD sẽ là trục đối xứng thứ hai. Đường thẳng này sẽ song song với các cạnh ngắn (BC và AD).
Hình chữ nhật có bao nhiêu trục đối xứng? Như vậy, hình chữ nhật có 2 trục đối xứng. Bạn có thể vẽ một hình chữ nhật, đánh dấu trung điểm của mỗi cạnh và kẻ hai đường thẳng qua các điểm này. Mỗi đường thẳng này sẽ chia hình chữ nhật thành hai nửa đối xứng (nửa trên, nửa dưới và nửa bên phải, nửa bên trái) qua mỗi trục.
| Trục đối xứng | Điểm qua | Song song với |
| Trục 1 | Trung điểm của BC và AD | Cạnh AB và CD |
| Trục 2 | Trung điểm của AB và CD | Cạnh BC và AD |
Xem ngay: Các dấu hiệu nhận biết hình chữ nhật hay, chi tiết
Mô tả chi tiết trục đối xứng của hình chữ nhật
Hình chữ nhật có hai trục đối xứng, mỗi trục đi qua trung điểm của hai cạnh đối diện và vuông góc với nhau. Cụ thể:
- Trục đối xứng thứ nhất: Đi qua trung điểm của hai cạnh ngắn hơn và song song với hai cạnh dài hơn. Điểm A (x1, y1) và A’ (x1′, y1′) trên cạnh này đối xứng qua trục, nghĩa là x1 = x1’ và y1 = -y1’ qua trục.
- Trục đối xứng thứ hai: Đi qua trung điểm của hai cạnh ngắn hơn và song song với hai cạnh dài hơn. Điểm B (x2, y2) và B’ (x2′, y2′) trên cạnh này đối xứng qua trục, nghĩa là x2 = x2’ và y2 = -y2’ qua trục.
Vẽ một hình chữ nhật và đánh dấu trung điểm của mỗi cạnh, sau đó kẻ hai đường thẳng qua các điểm này để thấy các trục đối xứng.
| Trục đối xứng | Điểm trên hình | Điểm phản chiếu |
| Trục 1 | A (x1, y1) | A’ (x1, -y1) |
| Trục 2 | B (x2, y2) | B’ (x1, -y2) |
Tìm hiểu: Cách tính diện tích hình chữ nhật đơn giản và dễ hiểu nhất
Lợi ích khi hiểu các trục đối xứng trong học tập và ứng dụng
Việc hiểu về trục đối xứng sẽ rất hữu ích trong nhiều lĩnh vực khác nhau. Dưới đây là cụ thể các lợi ích mà bạn có thể đạt được:
- Giải quyết vấn đề: Hiểu về trục đối xứng giúp học sinh và nhà thiết kế dễ dàng giải quyết các vấn đề về tính đối xứng, phát triển tư duy logic và kỹ năng phân tích.
- Ứng dụng trong kiến trúc và thiết kế: Trong kiến trúc, nghệ thuật và thiết kế sản phẩm, trục đối xứng giúp tạo ra các công trình hài hòa, cân đối, có tính thẩm mỹ cao.
- Giảng dạy: Giáo viên có thể sử dụng trục đối xứng như một công cụ để giúp học sinh hình dung và hiểu rõ hơn về các khái niệm toán học, khoa học tự nhiên.
Bài tập về trục đối xứng giúp học sinh rèn luyện tư duy, tăng cường khả năng ứng dụng kiến thức vào thực tiễn. Bên cạnh đó, hiểu về trục đối xứng còn giúp người học phát triển khả năng sáng tạo và giải quyết các tình huống phức tạp.

Ứng dụng trục đối xứng của hình chữ nhật trong thực tiễn
Trục đối xứng không chỉ là khái niệm trong hình học mà còn có nhiều ứng dụng thực tế quan trọng. Một số lĩnh vực nổi bật bao gồm:
- Kiến trúc: Trong thiết kế kiến trúc, trục đối xứng giúp tạo ra sự cân bằng và hài hòa. Nhiều công trình như lâu đài, nhà thờ, tòa nhà chính phủ thường có cấu trúc đối xứng.
- Nghệ thuật: Trong nghệ thuật, đối xứng là yếu tố quan trọng để tạo ra vẻ đẹp hài hòa và cân đối. Các tác phẩm nghệ thuật đối xứng thường thu hút, mang lại cảm giác thoải mái dễ chịu cho người xem.
- Công nghệ: Trong công nghệ, trục đối xứng được áp dụng trong thiết kế các bộ phận máy móc và thiết bị điện tử, giúp tối ưu hóa hiệu suất, độ bền của sản phẩm.
Ngoài ra, trục đối xứng còn xuất hiện trong tự nhiên và sinh học, ví dụ như sự đối xứng trong cấu trúc của động thực vật. Việc nghiên cứu, ứng dụng nguyên lý đối xứng đã mở ra nhiều cơ hội mới trong khoa học và kỹ thuật.
Vậy hình chữ nhật có mấy trục đối xứng? Câu trả lời là 2. Nếu còn thắc mắc nào khác, bạn đọc đừng ngần ngại để lại bình luận bên dưới để được đội ngũ chuyên gia giải đáp.
Nội dung bài viết
- 1. Định nghĩa về trục đối xứng
- 2. Trục đối xứng của hình chữ nhật là gì?
- 3. Hình chữ nhật có mấy trục đối xứng?
- 4. Ví dụ trực quan về trục đối xứng của hình chữ nhật
- 5. Mô tả chi tiết trục đối xứng của hình chữ nhật
- 6. Lợi ích khi hiểu các trục đối xứng trong học tập và ứng dụng
- 7. Ứng dụng trục đối xứng của hình chữ nhật trong thực tiễn




