Đường chéo hình vuông là kiến thức cơ bản trong hình học, có nhiều công dụng trong tính toán thực tiễn. Tuy nhiên các bạn học sinh thường không nắm chắc được và làm sai trong quá trình học. Hiểu rõ về tính chất và tham khảo các bài tập minh họa sẽ cải thiện đáng và giúp các em học sinh lấy lại căn bản nhanh chóng.
Tìm hiểu tính chất của đường chéo của hv
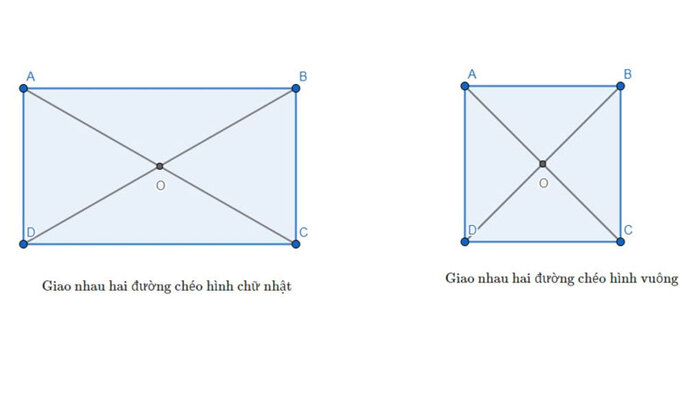
Hình vuông có hai đường chéo cắt nhau và chúng sẽ chia hình vuông thành 4 hình tam giác vuông cân bằng nhau. Các đường chéo đều sở sở hữu các tính chất sau:
- Đường chéo của hv luôn luôn bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
- Mỗi đường chéo là cạnh huyền của hai tam giác vuông cân.
- Hai đường chéo cắt nhau tạo thành 2 đường thẳng vuông góc.
Xem thêm: Hv là gì? Những tính chất của hình vuông
Cách tính đường chéo hình vuông
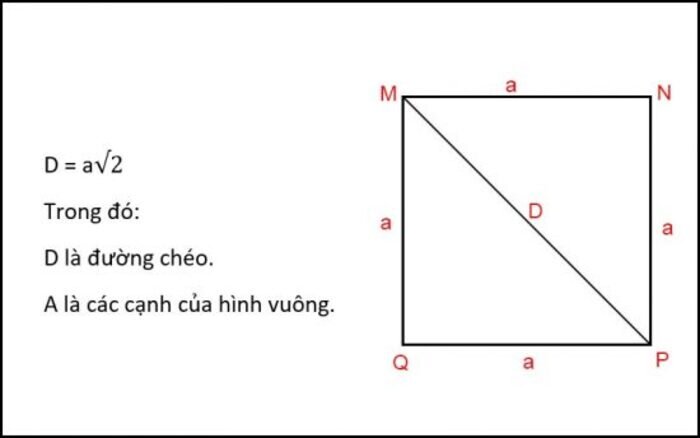
Khi có được độ dài của hình vuông, ta có thể áp dụng công thức tính của hình tam giác vuông để đo độ dài đường chéo trong hình vuông. Khi đó độ dài đường chéo là độ dài cạnh huyền của tam giác vuông cân, công thức tính sẽ như sau:
$$d=a\sqrt2$$
Trong đó: d là chiều dài cạnh huyền, a là chiều dài của một cạnh hình vuông.
Xem thêm: Dấu hiệu nhận biết hình vuông là gì?
Ví dụ bài toán cách tính đường chéo hình vuông
Áp dụng cách tính đường chéo hình vuông vào bài tập, xét ví dụ dưới đây:
Ví dụ 1: Cho một hình vuông có độ dài cạnh là 4cm. Hãy tính độ dài đường chéo hình vuông đó.
Áp dụng công thức d = a√2 vào bài toán, ta có chiều dài đường chéo của hình vuông đã cho như sau:
d = 4√2
Sử dụng máy tính bỏ túi thì kết quả sẽ bằng xấp xỉ 5,656 cm.
Ví dụ 2: Một mảnh đất hình vuông có chiều dài 1 cạnh là 6m. Người ta cần làm hàng rào để chia mảnh đất thành 2 khu hình tam giác bằng nhau. Hãy tính chiều dài của hàng rào đó.
Hàng rào cần thực hiện chính là đường chéo của hv. Áp dụng công thức sẽ có độ dài của hàng rào là: d = 6√2 ~ 8,485 m.
Xem thêm: Dạng bài tập chứng minh hình vuông
Ứng dụng tính chất trong thực tế
Trong thực tế, công thức tính đường chéo của hv được ứng dụng rất rộng rãi. Phổ biến nhất là ở các lĩnh vực như thiết kế, xây dựng, trang trí,… Cụ thể những ứng dụng này như sau:
- Trong xây dựng: Tính đường chéo hv chính xác giúp kiến trúc sư đảm bảo được bản vẽ thiết kế đúng, khi thi công sẽ an toàn, vuông vức và đẹp mắt.
- Trong thiết kế nội thất: Tối ưu hoá không gian là vấn đề quan trọng mà bất cứ công trình nào cũng cần chú ý. Việc tính toán đường chéo sẽ giúp kiến trúc sư biết được vị trí sắp xếp các vật dụng, đảm bảo hiệu quả sử dụng và tính thẩm mỹ.
- Trong khoa học công nghệ: Tất cả các thiết bị điện tử có sử dụng màn hình hiện nay đều áp dụng công thức tính đường chéo để làm đơn vị đo lường màn hình hiển thị.
- Trong bản đồ và đo đạc: Nhờ có đường chéo, ta cũng có thể dễ dàng ước lượng một cách chính xác diện tích, khoảng cách của mảnh đất nhỏ hay của một vùng rộng lớn.

Lý thuyết toán học đằng sau công thức tính đường chéo hv
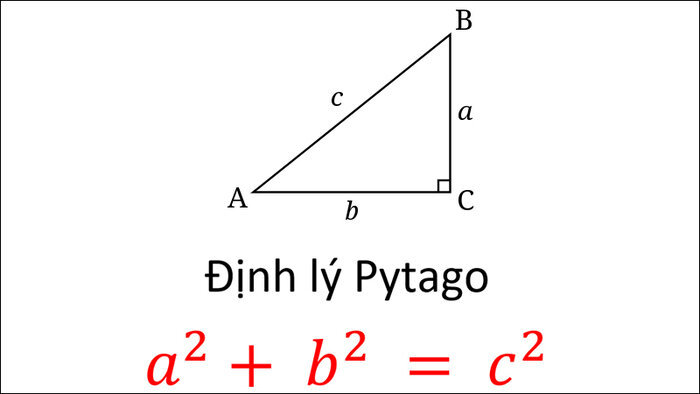
Công thức tính đường chéo hình vuông hiện nay được phát triển từ định lý Pythagoras. Đây là định lý được nhà toán học Pythagoras công bố và là một trong những định lý cơ bản nhất của hình học.
Khi định lý Pythagoras áp dụng cho tam giác vuông, ta có bình phương của cạnh huyền sẽ bằng tổng bình phương của hai cạnh góc vuông. Trong một hv, đường chéo sẽ chia nó thành hai tam giác vuông bằng nhau. Mỗi một cạnh hv tương ứng là 1 cạnh của tam giác vuông, đường chéo sẽ là cạnh huyền. Từ đó áp dụng công thức tính cạnh huyền sẽ tính được đường chéo hình vuông bằng a√2.
Với lý thuyết Pythagoras, ta có thể thấy dễ dàng cách tính đường chéo hv mà không cần phải nhớ công thức một cách máy móc. Nó cũng phản ánh được tính đối xứng và hài hoà của hv khi hai đường chéo bằng nhau, cắt nhau tại trung điểm mỗi đường và tạo với nhau góc 90 độ. Có thể nói đây là tính chất đặc biệt mà chỉ hình vuông mới có.
Xem thêm: Cách tính diện tích hình vuông
Mẹo nhớ công thức tính đường chéo hv đơn giản nhất
Công thức tính đường chéo hình vuông là a√2. Tuy nhiên nếu công thức này khó nhớ, bạn có thể sử dụng một số mẹo đơn giản nhưng hiệu quả tốt. Cụ thể như sau:
- Nhớ công thức đường chéo hv máy móc, chỉ cần lấy cạnh của hv nhân với √2 là ra kết quả.
- Nhớ công thức dựa vào định lý Pythagoras. Biết rằng đường chéo sẽ chia đôi hv và tạo thành 2 tam giác vuông cân. Từ đó có thể coi đường này là cạnh huyền. Tính cạnh huyền tam giác vuông cân sẽ ra được kết quả độ dài đường chéo hv.
Trên đây là bài viết thông tin chi tiết về đường chéo của hình vuông. Những thông tin này sẽ giúp ích rất nhiều cho bạn đọc trong tiến trình học tập cũng như ứng dụng thực tế sắp tới. Nếu có bất kỳ thắc mắc hay ý tưởng mới mẻ, hãy bình luận ngay bên dưới nhé!