Cách chứng minh hình tam giác đều chi tiết, đơn giản nhất

Chứng minh hình tam giác đều là dạng toán thường gặp trong hình học. Từ những dấu hiệu nhận biết, bạn có thể chứng minh hình theo đề bài đưa ra. Một số hướng dẫn chi tiết và đơn giản nhất mà học sinh và bạn đọc có thể áp dụng.

Giới thiệu về tam giác đều

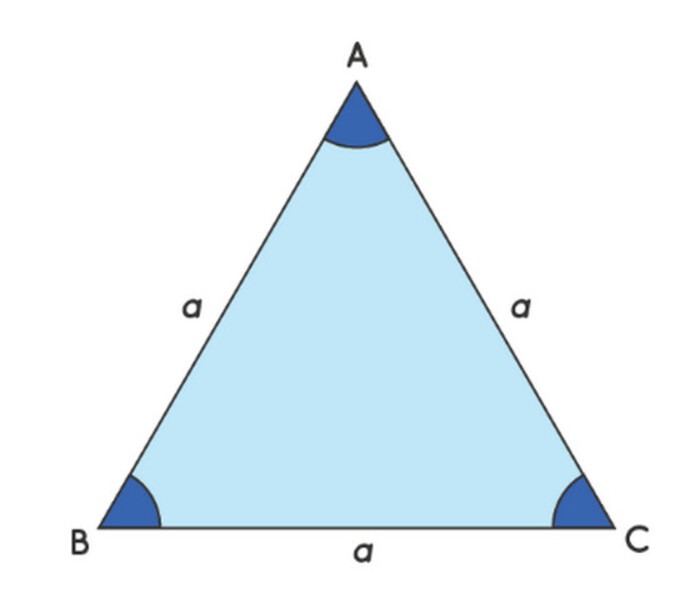
Tam giác đều là một hình tam giác có tính đối xứng tuyệt đối với 3 cạnh bằng nhau, 3 góc bằng nhau và bằng 60 độ.

Xem thêm: Định nghĩa, tính chất của hình tam giác cân

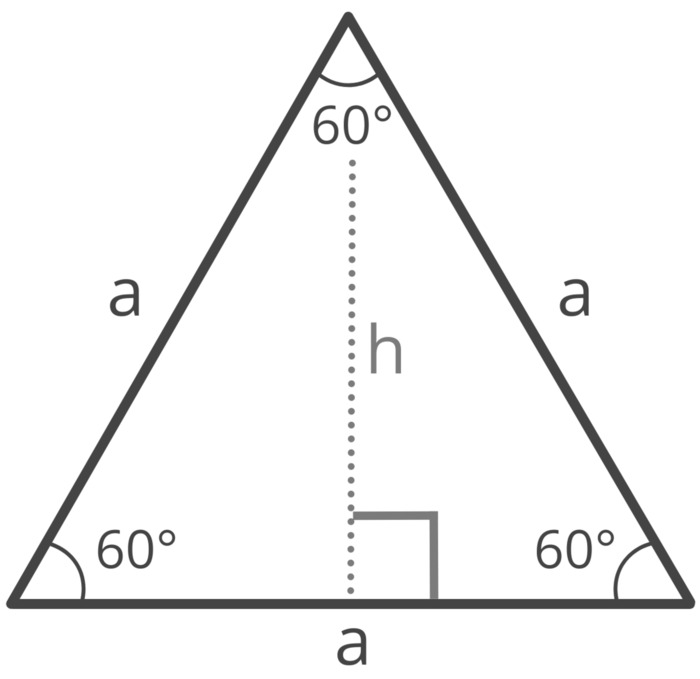
Cách chứng minh hình tam giác đều chi tiết

Cách chứng minh hình tam giác đều sẽ xoay quanh các tính chất của hình tam giác. Trong đó một số phương pháp phổ biến nhất là chứng minh 3 cạnh tam giác bằng nhau, 3 góc trong bằng nhau hoặc sử dụng định lý Pytago. Chi tiết các phương pháp sẽ như sau:

Phương pháp 1: Chứng minh ba cạnh bằng nhau

Với phương pháp này, ta cần chứng minh các cạnh của hình tam giác có độ dài bằng nhau. Từ đó suy ra đây là hình tam giác đều. Tuỳ vào dữ kiện của đề bài mà sẽ có các bước làm khác nhau. Phương pháp phổ biến thường sử dụng nhất là định lý Pythagoras. Cách thực hiện như sau:

• Bước 1: Vẽ hình tam giác và xác định tọa độ. Tam giác ABC có các đỉnh tọa độ là A(x1,y1); B(x2,y2); C(x3,y3).
• Bước 2: Áp dụng công thức khoảng cách Euclide để tìm ra chiều dài của các cạnh như sau:

Độ dài cạnh AB:

$$\mathrm{dA}B=\sqrt{(x2-x1{)}^2+(y2-y1{)}^{\mathrm{2<span\; style="font-family:\; Arial,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;\; font-size:\; 16px;"></span>}}}$$

Độ dài cạnh BC:

$$\mathrm{dB}C=\sqrt{(x3-x2{)}^2+(y3-y2{)}^{\mathrm{2<span\; style="font-family:\; Arial,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;\; font-size:\; 16px;"></span>}}}$$

Độ dài cạnh CA:

$$\mathrm{dC}A=\sqrt{(x3-x1{)}^2+(y3-y1{)}^{\mathrm{2<span\; style="font-family:\; Arial,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;\; font-size:\; 16px;"></span>}}}$$

• Bước 3: So sánh kết quả độ dài 3 cạnh. Nếu chúng bằng nhau thì đây là tam giác đều.

Phương pháp 2: Chứng minh ba góc bằng nhau

Ngoài chứng minh các cạnh, ta có thể chứng minh tam giác có 3 góc bằng nhau là tam giác đều. Tổng 3 góc trong của tam giác là 180 độ, nên suy ra mỗi góc trong tam giác là 60 độ. Khi đã có tam giác với 2 góc là 60 độ thì chắc chắn đây là một hình tam giác đều.

Phương pháp 3: Chứng minh tam giác cân và có một góc bằng 60°

Nếu là một hình tam giác cân, hai cạnh bên bằng nhau thì hai góc tạo bởi các cạnh bên với cạnh đáy cũng sẽ bằng nhau. Nếu tam giác có một góc bằng 60 độ thì chắc chắn hai góc còn lại cũng sẽ là 60 độ. Do đó nếu chứng minh được tam giác cân có 1 góc bằng 60 độ thì đây sẽ là tam giác đều.

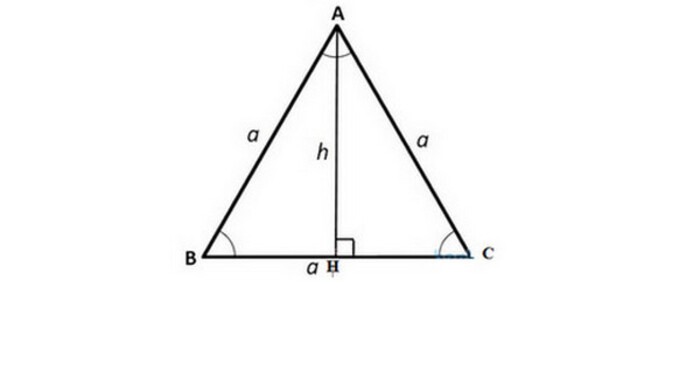
Phương pháp 4: Chứng minh từ tính chất đường trung tuyến

Trong một tam giác đều, các đường trung tuyến sẽ vừa là đường cao, vừa là đường phân giác và cũng là đường trung trực. Đường thẳng này sẽ chia tam giác đều thành hai tam giác bằng nhau. Nếu chứng minh được đường trung tuyến vừa là các đường trên thì có thể khẳng định đó là hình tam giác đều.

Công thức áp dụng để chứng minh hình tam giác đều trong trường hợp này như sau:

• Công thức định lý sin và cos để tính ra độ dài cạnh và góc.
• Sử dụng thước và các thiết bị đo đạc chính xác trong thực nghiệm để tính ra các cạnh và các góc.

Xem thêm: Cách tính đường cao hình tam giác

Bài tập ví dụ các bước chứng minh tam giác đều

Để áp dụng phương pháp chứng minh tam giác đều được nhanh và tốt nhất, bạn có thể lưu ý luyện tập đều đặn với dạng bài tập như dưới đây:

Bài tập 1: Dùng các công cụ như thước kẻ để đo độ dài các cạnh hình. Tam giác đó có đều hay không?

Gợi ý giải: Với hình tam giác đề bài đã cho, sử dụng thước đo sẽ thấy chiều dài của cả 3 cạnh đều cùng một độ dài. Do đó đây là một hình tam giác đều.

Bài tập 2: Vẽ một tam giác ABC đều

Gợi ý giải: Sử dụng thước kẻ, compa hoặc thước đo độ để vẽ. Vẽ một đoạn thẳng với chiều dài là a, dùng thước đo góc vẽ góc 60 độ, sau đó một cạnh bằng với cạnh ban đầu, Cuối cùng nối 2 điểm còn lại với nhau tạo thành tam giác đều.

Bài tập 3: Cho tam giác ABC là tam giác đều, chứng minh $$AB^2\;+\;AC^2=BC^2$$

Gợi ý giải: Áp dụng định lý Pytago trong một tam giác đều để chứng minh.

Ứng dụng của tam giác đều trong thực tế

Không chỉ áp dụng trong làm bài toán học, các cách chứng minh hình tam giác đều còn có nhiều ứng dụng hữu ích trong cuộc sống. Cụ thể chúng được ứng dụng trong các lĩnh vực như sau:

• Ngành kiến trúc: Những thiết kế yêu cầu tính đối xứng cao rất cần áp dụng bố cục tam giác đều. Như vậy sẽ đảm bảo được sự thẩm mỹ cho không gian.
• Ngành kỹ thuật: Trong quy trình sản xuất hàng hoá, máy móc, thiết bị, sự chính xác là vô cùng cần thiết. Có những công đoạn đòi hỏi tính chính xác tuyệt đối. Nguyên tắc cân bằng của tam giác đều sẽ giúp đạt được hiệu quả tối ưu
• Ngành thiết kế đồ hoạ: Trong khi thiết kế, ứng dụng tính đối xứng của tam giác đều cũng tạo nên những tác phẩm có tính cân đối và hài hoà. Trong đó trọng tâm tam giác đều được ứng dụng làm điểm cân bằng nhiều nhất.
• Ngành khoa học tự nhiên: Nhiều hiện tượng khoa học được chứng minh có liên quan đến cấu trúc của tam giác đều như hiện tượng quang học,…

Hiểu rõ về hình tam giác đều và áp dụng những cách chứng minh hình tam giác đều sẽ giúp các em học sinh ứng dụng được vào bài tập hiệu quả. Học toán dễ dàng hơn bao giờ hết khi nắm chắc những kiến thức từ cơ bản đến nâng cao tại hocthenao.vn.