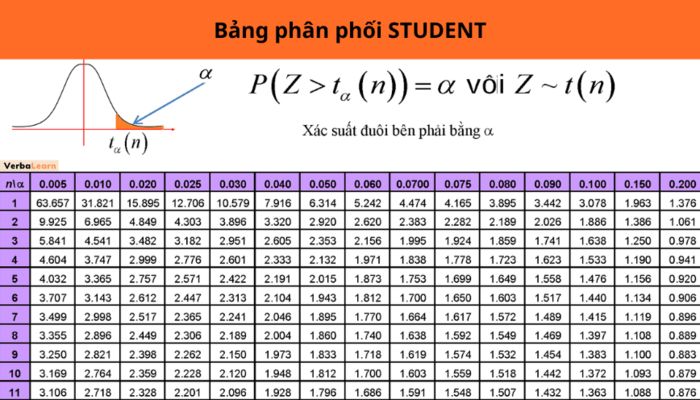
Bảng phân phối Student là một phân phối xác suất liên tục được sử dụng rộng rãi trong các môn học đại cương của ngành kinh tế học, đặc biệt là: Xác suất thống kê và Kinh tế lượng. Nội dung này được đánh giá là có khối lượng kiến thức khổng lồ và rất khó tiếp cận với không ít người. Bài viết dưới đây, chúng tôi sẽ cung cấp cho các bạn đầy đủ thông tin về nội dung này.
Bảng phân phối Student là gì?
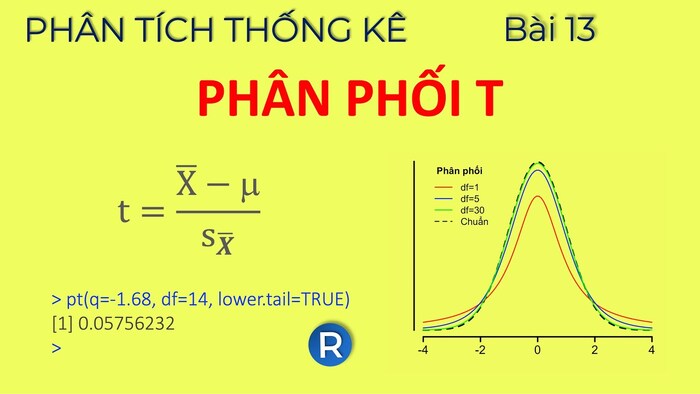
Bảng phân phối Student (bảng phân phối t) là một biểu diễn mối quan hệ giữa xác suất (hay vùng diện tích dưới đường cong phân phối) và giá trị quan sát t, với các bậc tự do khác nhau. Đây là bảng thống kê quan trọng được sử dụng rộng rãi trong nhiều lĩnh vực nghiên cứu và phân tích dữ liệu.
Phân phối Student được đặt tên theo nhà toán học William Sealy Gosset, người đã phát triển ra phân phối này vào đầu thế kỷ 20 khi làm việc cho nhà máy bia Guinness ở Dublin, Ai-len. Ông đã sử dụng bút danh “Student” khi công bố nghiên cứu của mình về phân phối xác suất này, do đó nó mang tên gọi hiện nay. Tên trong tiếng anh là T Distribution hay Student’s t-distribution.
Bảng Student trong xác suất thống kê có rất nhiều ứng dụng, đặc biệt là khi làm việc với mẫu nhỏ và phương sai của tổng thể chưa được biết. Nó được sử dụng để tính toán xác suất, khoảng tin cậy, kiểm định giả thuyết và nhiều tình huống khác liên quan đến suy luận thống kê.
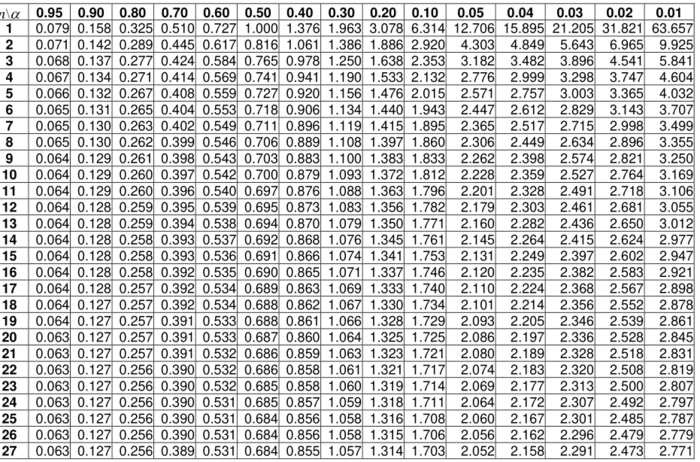
Bảng phân phối Student đầy đủ
Bảng phân phối Student PDF sẽ được chúng tôi cung cấp ngay sau đây:
Cách Tra bảng phân phối Student đơn giản
Dưới đây là quy trình tra bảng tra Student dễ dàng và chính xác nhất.
Bước 1: Xác định bậc tự do
Cách tra bảng Student, điều đầu tiên cần làm là xác định bậc tự do (degrees of freedom). Bậc tự do phản ánh kích thước mẫu và được tính bằng công thức n – 1, trong đó n là số lượng quan sát trong mẫu. Ví dụ, nếu có 15 quan sát trong mẫu, bậc tự do sẽ là 15 – 1 = 14.
Bước 2: Xác định giá trị t quan sát
Tiếp theo, cần xác định giá trị quan sát t. Giá trị quan sát t là giá trị thống kê mà chúng ta cần tìm xác suất hoặc vùng diện tích tương ứng trên đường cong phân phối Student. Giá trị này có thể được tính từ dữ liệu mẫu hoặc được cho sẵn trong bài toán.
Bước 3: Tìm hàng và bậc tương ứng
Sau khi có bậc tự do và giá trị quan sát t, bước tiếp theo là tìm hàng tương ứng với bậc tự do đã xác định trong bảng t Student. Sau đó, di chuyển ngang qua các cột cho đến khi gặp giá trị quan sát t gần nhất với giá trị đã cho.
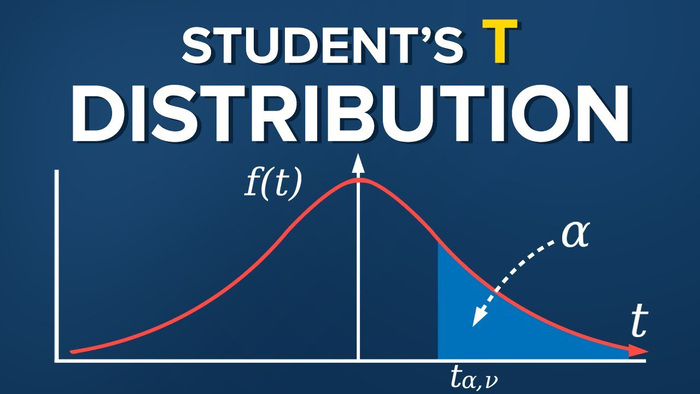
Bước 4: Xác định xác suất hoặc vùng diện tích
Điểm giao giữa hàng bậc tự do và cột giá trị quan sát t trong bảng phân vị Student sẽ cho ta xác suất hoặc vùng diện tích tương ứng dưới đường cong phân phối Student. Cần lưu ý rằng bảng tra t thường cung cấp vùng diện tích một phía (one-tailed area), tức vùng diện tích từ vô cùng về phía trái đến giá trị quan sát t.
Bước 5: Tính xác suất 2 phía(nếu cần)
Nếu cần tìm xác suất hai phía (two-tailed area), chỉ cần nhân đôi xác suất một phía đã tìm được ở bước trước. Ví dụ, nếu xác suất một phía là 0,025, thì xác suất hai phía sẽ là 0,025 * 2 = 0,05 hoặc 5%.
Quy trình sử dụng bảng tra phân phối Student đòi hỏi sự cẩn thận và chính xác, đảm bảo rằng chúng ta đang sử dụng đúng bậc tự do, giá trị quan sát t và hiểu rõ ý nghĩa của xác suất hoặc vùng diện tích thu được. Từ đó, chúng ta có thể áp dụng kết quả để giải quyết các vấn đề liên quan đến kiểm định giả thuyết, tính khoảng tin cậy và các bài toán thống kê khác.
Các tính chất quan trọng của bảng Student
Bảng phân phối Student đầy đủ có các tính chất quan trọng sau:
Hình dạng phân phối
Một tính chất quan trọng của bảng tra Student là bậc tự do (degrees of freedom). Bậc tự do ảnh hưởng đến hình dạng của phân phối. Khi bậc tự do tăng lên, đường cong phân phối Student trở nên nhọn hơn và tiệm cận về phân phối chuẩn. Ngược lại, khi bậc tự do giảm xuống, đường cong phân phối Student trở nên dẹt hơn và có đuôi dày hơn.
Tâm và đối xứng
Phân phối Student là một phân phối đối xứng quanh tâm 0 và xác định trên toàn bộ trục thực, từ âm vô cùng đến dương vô cùng. Một tính chất quan trọng khác là khi bậc tự do tiến về vô cùng, phân phối Student sẽ tiệm cận về phân phối chuẩn tiêu chuẩn. Tuy nhiên, khi bậc tự do nhỏ, phân phối Student sẽ khác xa so với phân phối chuẩn.
Phạm vi giá trị
Bảng Student PDF được sử dụng rộng rãi trong thống kê suy luận, đặc biệt là khi làm việc với mẫu nhỏ và phương sai của tổng thể chưa được biết. Nó được áp dụng trong các bài toán kiểm định giả thuyết, tính khoảng tin cậy, phân tích hồi quy, và nhiều tình huống khác liên quan đến suy luận thống kê. Những tính chất độc đáo của phân phối Student làm cho nó trở nên rất hữu ích và được sử dụng phổ biến trong nhiều lĩnh vực nghiên cứu và phân tích dữ liệu.
Ứng dụng của bảng phân phối T trong thực tiễn
Bảng phân bố Student có nhiều ứng dụng quan trọng trong lĩnh vực thống kê suy luận. Dưới đây là một số ứng dụng chính:
Tìm khoảng tin cậy
Một trong những ứng dụng phổ biến nhất của bảng Student là tính toán khoảng tin cậy cho giá trị trung bình của tổng thể khi phương sai của tổng thể chưa được biết và kích thước mẫu nhỏ. Bằng cách sử dụng bảng phân phối Student, chúng ta có thể xác định khoảng tin cậy cho giá trị trung bình tổng thể dựa trên giá trị trung bình mẫu, độ lệch chuẩn mẫu và bậc tự do.
Kiểm định giả thuyết
Bảng pp Student cũng được sử dụng rộng rãi trong kiểm định giả thuyết về giá trị trung bình của tổng thể khi phương sai tổng thể chưa biết và kích thước mẫu nhỏ. Quy trình này bao gồm việc tính toán giá trị quan sát t, sau đó so sánh với giá trị quan sát t tới hạn từ bảng phân phối Student để quyết định có chấp nhận hay bác bỏ giả thuyết hay không.
Phân tích hồi quy tuyến tính
Ngoài ra, bảng t còn được áp dụng trong phân tích hồi quy tuyến tính, đặc biệt là khi kiểm tra tính đáng tin cậy của các hệ số hồi quy. Trong trường hợp này, các giá trị quan sát t được tính từ các hệ số hồi quy và sai số chuẩn của chúng, sau đó so sánh với giá trị quan sát t tới hạn từ bảng tra Student để đánh giá tính đáng tin cậy của các hệ số.
Lời kết
Tóm lại, bảng phân phối Student là một công cụ hữu ích và quan trọng trong thống kê suy luận, đặc biệt khi làm việc với mẫu nhỏ và phương sai của tổng thể chưa được biết. Nó giúp các nhà nghiên cứu và chuyên gia thống kê đưa ra các kết luận đáng tin cậy dựa trên dữ liệu mẫu.