Cát tuyến là gì cùng cách vẽ, tính chất và ứng dụng trong hình học

Cát tuyến là gì là một khái niệm quan trọng trong hình học, giúp bạn hiểu rõ về mối liên hệ giữa các hình và các tính chất của chúng. Khám phá cát tuyến không chỉ đơn thuần là lý thuyết, mà còn mang đến ứng dụng thực tế trong giải toán. Hãy tiếp tục theo dõi để nắm vững kiến thức và cách áp dụng hiệu quả.

Cát tuyến là gì?

Cát tuyến là gì – một loại tuyến nội tiết nằm ở vùng cổ, phía trước khí quản và ngay dưới thanh quản. Tuyến này có hình dạng giống con bướm với hai thùy bên được nối với nhau bởi eo tuyến, có màu nâu đỏ và kích thước khoảng 4-6cm.

Đây là một trong những tuyến nội tiết quan trọng nhất của cơ thể, đóng vai trò sản xuất và tiết ra các hormone điều hòa quá trình trao đổi chất. Khi được hỏi “cát tuyến là j“, các bác sĩ thường giải thích đây chính là tuyến giáp – một bộ phận không thể thiếu trong việc duy trì sự sống của con người.

Tuyến này sản xuất ra hai loại hormone chính là T3 (triiodothyronine) và T4 (thyroxine), tham gia vào nhiều quá trình sinh lý quan trọng như điều hòa nhịp tim, huyết áp, nhiệt độ cơ thể và tốc độ trao đổi chất. Ngoài ra, cát tuyến còn đóng vai trò thiết yếu trong sự phát triển não bộ của thai nhi và trẻ nhỏ.

Các tính chất quan trọng của cát tuyến trong hình học phẳng

Cát tuyến là một khái niệm quan trọng trong hình học phẳng, có nhiều ứng dụng trong việc giải các bài toán hình học. Để hiểu rõ về tính chất cát tuyến, cần nắm vững các đặc điểm và mối quan hệ của nó với các yếu tố hình học khác.

Định nghĩa và đặc điểm cơ bản của cát tuyến

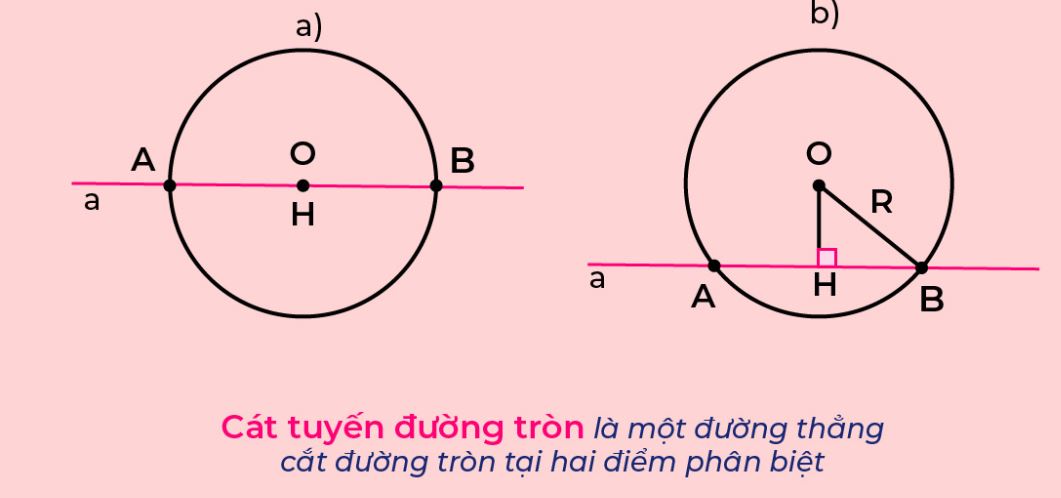
Cát tuyến là đường thẳng cắt một đường tròn tại hai điểm phân biệt. Khác với đường trung tuyến là gì, cát tuyến không nhất thiết phải đi qua tâm đường tròn. Khoảng cách từ tâm đường tròn đến cát tuyến luôn nhỏ hơn bán kính đường tròn.

Một đặc điểm quan trọng của cát tuyến là nó tạo ra hai dây cung bằng nhau trên đường tròn. Điều này dẫn đến việc hai góc tạo bởi cát tuyến và tiếp tuyến tại điểm cắt cũng bằng nhau.

Mối quan hệ giữa cát tuyến và đường tròn

Khi một cát tuyến cắt đường tròn, nó tạo ra hai điểm cắt và chia đường tròn thành hai phần. Khoảng cách từ tâm đường tròn đến cát tuyến có mối liên hệ với bán kính đường tròn thông qua công thức Pythagore.

Nếu khoảng cách từ tâm đến cát tuyến tiến dần đến bán kính, cát tuyến sẽ tiến dần đến vị trí tiếp tuyến của đường tròn. Ngược lại, nếu khoảng cách này tiến về 0, cát tuyến sẽ trở thành đường kính.

Tính chất đặc biệt của cát tuyến trong tam giác

Cát tuyến trong tam giác có những tính chất độc đáo khi tam giác được nội tiếp hoặc ngoại tiếp trong đường tròn. Khi một cát tuyến đi qua một đỉnh của tam giác nội tiếp, nó sẽ chia cạnh đối diện thành hai phần có tỷ số nhất định.

Trong trường hợp tam giác ngoại tiếp, các cát tuyến của đường tròn nội tiếp tạo với các cạnh tam giác những đoạn có tích không đổi. Tính chất này thường được áp dụng để giải các bài toán về tỷ số và diện tích trong tam giác.

Hướng dẫn chi tiết cách vẽ và xác định cát tuyến

Để vẽ và xác định cát tuyến chính xác, người học cần nắm vững các nguyên tắc cơ bản và thực hiện theo trình tự các bước. Việc xác định cát tuyến đóng vai trò quan trọng trong việc phân tích lực và chuyển động của vật thể trong không gian.

Các bước vẽ cát tuyến chuẩn xác

Bước đầu tiên khi vẽ cát tuyến là xác định điểm đặt lực và hướng tác dụng của lực. Điều này giúp định hình được vị trí và phương của cát tuyến cần vẽ. vecto pháp tuyến là gì sẽ giúp xác định chính xác góc nghiêng của cát tuyến.

Tiếp theo, cần vẽ đường thẳng vuông góc với phương của lực tại điểm đặt. Đường thẳng này chính là cách vẽ cát tuyến cơ bản nhất. Độ dài của cát tuyến được xác định bằng khoảng cách từ điểm đặt lực đến giao điểm với phương của lực.

Phương pháp xác định điểm cát tuyến

Việc xác định điểm cát tuyến đòi hỏi sự chính xác cao trong phép đo và tính toán. Điểm cát tuyến thường được xác định thông qua phép chiếu vuông góc từ điểm đặt lực lên phương của lực.

Khi xác định điểm cát tuyến, cần chú ý đến góc giữa phương của lực và đường thẳng vuông góc. Góc này phải đảm bảo đúng 90 độ để tạo ra cát tuyến là gì chính xác nhất trong bài toán.

Trong nhiều trường hợp, việc xác định điểm cát tuyến có thể được hỗ trợ bởi các công cụ đo lường hoặc phần mềm chuyên dụng, giúp tăng độ chính xác của kết quả.

Những lưu ý khi vẽ cát tuyến

Khi vẽ cát tuyến, độ chính xác của các phép đo và tính toán góc là yếu tố then chốt. Sai số nhỏ trong quá trình vẽ có thể dẫn đến kết quả sai lệch đáng kể.

Công cụ vẽ như thước, compa cần được chuẩn bị đầy đủ và đảm bảo chất lượng. Việc sử dụng các công cụ này đúng cách sẽ giúp tạo ra các đường nét chính xác và rõ ràng.

Ngoài ra, cần kiểm tra lại kết quả sau khi vẽ bằng cách đo đạc lại các góc và khoảng cách. Điều này giúp phát hiện và điều chỉnh các sai sót có thể xảy ra trong quá trình thực hiện.

Ứng dụng của cát tuyến trong giải toán hình học

Cát tuyến đóng vai trò quan trọng trong việc giải các bài toán hình học phức tạp. Việc nắm vững các công thức cát tuyến giúp học sinh có thêm công cụ hiệu quả để giải quyết nhiều dạng toán về tam giác và tứ giác.

Theo Học Thế Nào, việc áp dụng cát tuyến trong giải toán không chỉ giúp rút ngắn thời gian giải mà còn mang lại cách tiếp cận mới, sáng tạo hơn cho nhiều bài toán tưởng chừng phức tạp.

Các công thức liên quan đến cát tuyến

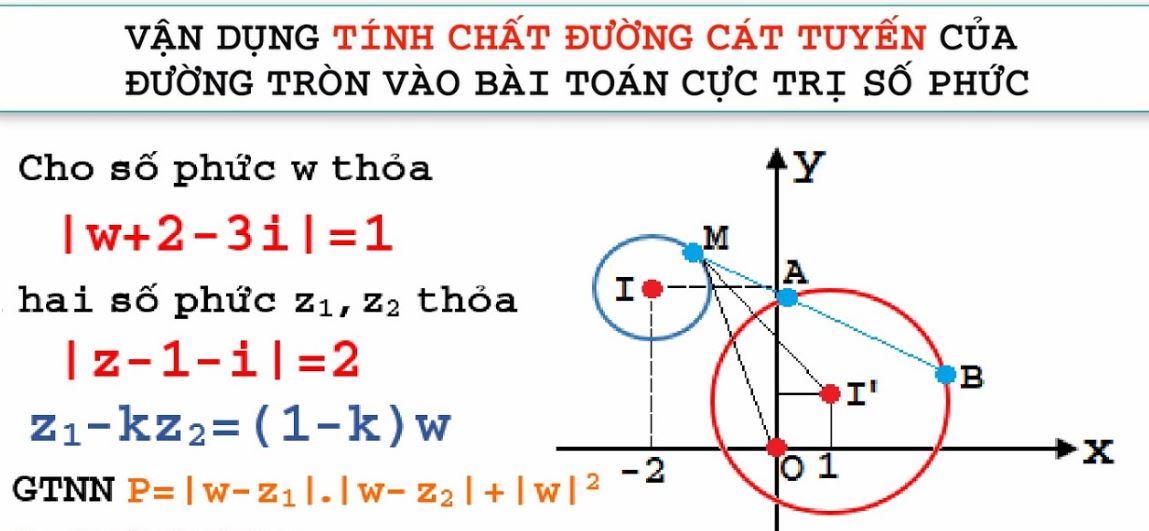
Trong tam giác ABC, nếu D là điểm nằm trên BC thì AD được gọi là cát tuyến. Tỷ số của các đoạn thẳng trên cát tuyến tuân theo các quy luật nhất định và có mối liên hệ chặt chẽ với diện tích các tam giác tạo thành.

Khi áp dụng các ứng dụng cát tuyến, ta cần chú ý đến tỷ số phân chia của cát tuyến trên cạnh tam giác. Điều này giúp thiết lập các phương trình và bất phương trình để tìm ra lời giải.

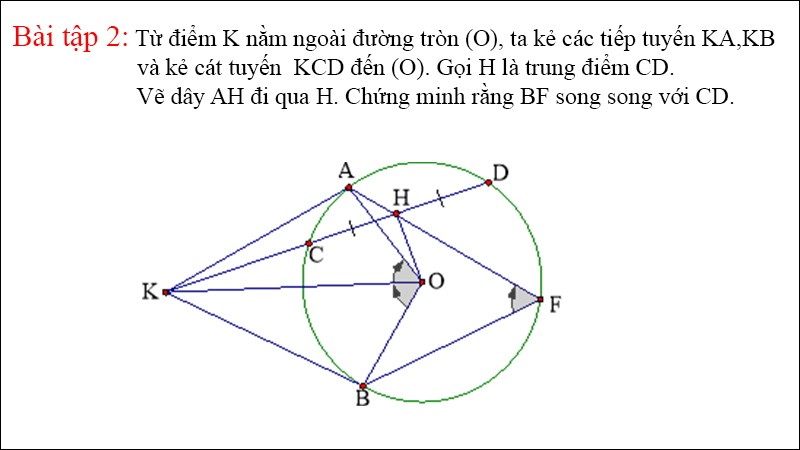
Bài tập áp dụng về cát tuyến

Để vận dụng tốt kiến thức về cát tuyến, học sinh cần thực hành qua nhiều dạng bài tập đa dạng. Các bài toán thường yêu cầu tìm tỷ số phân chia, chứng minh đường thẳng là cát tuyến hoặc tính toán các yếu tố liên quan.

Việc giải các bài tập về cát tuyến đòi hỏi sự linh hoạt trong tư duy và khả năng kết hợp nhiều kiến thức hình học. Học sinh cần rèn luyện kỹ năng nhận diện và vận dụng các định lý cát tuyến phù hợp với từng dạng bài.

Định lý quan trọng về cát tuyến

Định lý về cát tuyến trong tam giác là nền tảng quan trọng để giải quyết nhiều bài toán phức tạp. Định lý này khẳng định mối quan hệ giữa độ dài các đoạn thẳng được tạo ra khi cát tuyến chia cạnh tam giác thành các phần tỷ lệ.

Ngoài ra, định lý về trọng tâm tam giác cũng liên quan mật thiết đến cát tuyến, khi ba cát tuyến từ ba đỉnh đến trung điểm các cạnh đối diện đồng quy tại một điểm và chia nhau theo tỷ số 2:1.

Mối quan hệ giữa cát tuyến và đường tròn trong hình học

Cát tuyến của đường tròn là đường thẳng cắt đường tròn tại hai điểm phân biệt. Mối quan hệ giữa cát tuyến và đường tròn thể hiện qua việc cát tuyến tạo ra hai dây cung bằng nhau khi cắt đường tròn.

Khi một đường thẳng cắt đường tròn, nó có thể tạo thành tiếp tuyến hoặc cát tuyến. Cát tuyến và đường tròn có mối liên hệ đặc biệt thông qua định lý về độ dài các đoạn cát tuyến kẻ từ một điểm ngoài đường tròn.

Trong không gian ba chiều, cát tuyến là gì còn được mở rộng để mô tả đường thẳng cắt mặt cầu. Điều này cho thấy tầm quan trọng của khái niệm cát tuyến trong hình học không gian.

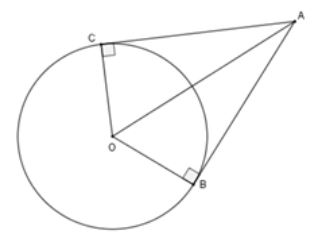
Cát tuyến của đường tròn và các tính chất

Một trong những tính chất quan trọng nhất của cát tuyến là định lý về tích các đoạn cát tuyến. Nếu từ một điểm P nằm ngoài đường tròn kẻ hai cát tuyến cắt đường tròn tại các cặp điểm A, B và C, D thì PA × PB = PC × PD.

Tính chất thứ hai liên quan đến góc giữa cát tuyến và tiếp tuyến. Khi cát tuyến của đường tròn cắt tiếp tuyến tại một điểm, góc tạo bởi cát tuyến và tiếp tuyến bằng góc trong đường tròn ở phía đối diện.

Ngoài ra, cát tuyến còn có tính chất về đường vuông góc. Đường vuông góc từ tâm đến cát tuyến là đường trung trực của dây cung tạo bởi cát tuyến đó.

Ứng dụng trong các bài toán về đường tròn

Cát tuyến được ứng dụng rộng rãi trong việc giải các bài toán về đường tròn. Trong xây dựng, kiến trúc sư thường sử dụng tính chất của cát tuyến để thiết kế các cấu trúc hình tròn và vòm.

Trong thiết kế công nghiệp, nguyên lý về cát tuyến giúp tính toán góc cắt chính xác cho các chi tiết máy có dạng hình tròn. Ví dụ, công ty Boeing áp dụng tính chất cát tuyến trong thiết kế cánh máy bay để tối ưu khí động học.

Lĩnh vực quang học cũng áp dụng các tính chất của cát tuyến trong thiết kế thấu kính và gương cầu. Các nhà khoa học sử dụng mối quan hệ giữa cát tuyến và đường tròn để tính toán đường đi của tia sáng.

Phương pháp giải các dạng bài tập liên quan

Để giải các bài tập về cát tuyến, cần nắm vững các bước cơ bản sau:

• Xác định vị trí tương đối giữa điểm và đường tròn
• Áp dụng định lý về tích các đoạn cát tuyến
• Sử dụng các tính chất về góc và đường vuông góc

Khi giải bài tập phức tạp, việc vẽ hình chính xác và đầy đủ các yếu tố cho trước rất quan trọng. Điều này giúp nhận diện được các quan hệ hình học cần thiết.

Một phương pháp hiệu quả là chuyển bài toán về cát tuyến thành bài toán về tam giác đồng dạng. Cách

Cát tuyến là khái niệm quan trọng trong hình học, giúp người học hiểu rõ hơn về các hình học phẳng và đường tròn. Thông qua các tính chất, cách vẽ và ứng dụng của cát tuyến, bạn sẽ nắm bắt được những kiến thức cần thiết để giải quyết các bài toán hình học một cách hiệu quả. Việc nắm vững cát tuyến là gì không chỉ giúp bạn học tốt môn toán mà còn tăng cường khả năng tư duy logic.