Chéo hóa ma trận là gì? Bài tập và phương pháp giải

Chéo hoá ma trận có thể được hiểu là quá trình đi tìm ma trận chéo hoá B và ma trận nghịch đảo T trong đại số và hình học giải tích. Các dạng toán liên quan đến chủ đề này thường không quá khó, mấu chốt để giải là chúng ta cần phải nắm được các giá trị riêng và các vectơ riêng của ma trận. Bài viết dưới đây sẽ hướng dẫn bạn từng bước chi tiết, từ định nghĩa, lý thuyết, đến các ví dụ và ứng dụng thực tế, giúp bạn hiểu rõ và thành thạo kỹ thuật Toán học này.

Chéo hoá ma trận là gì?

Chéo hóa ma trận là quá trình biến đổi ma trận vuông (A) thành ma trận chéo (B) thông qua ma trận chuyển đổi (T) sao cho thỏa mãn điều kiện B = T^-1AT. Từ đó, ta có thể nói ma trận T làm chéo hoá ma trận A và ma trận B là dạng ma trận chéo của A. Hay nói cách khác, kỹ thuật chéo hoá ma trận A là tìm ra ma trận nghịch đảo T và trở thành ma trận chéo B.

Ta có: $$A=TBT^{-1}$$

Nếu ta cần tính An thì dựa theo công thức như sau:

$$A^n={(TBT^{-1})}^n=TB^nT^{-1}$$

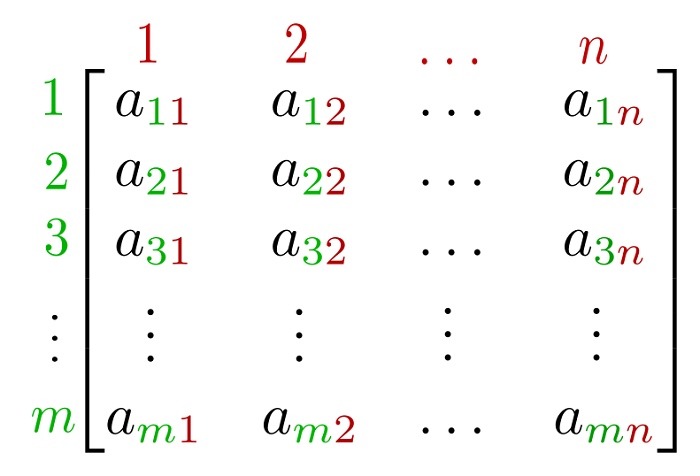
Các khái niệm cơ bản

Để giải được các bài toán về ma trận nói chung và ma trận chéo hoá nói riêng, bạn cần nắm được các khái niệm cơ bản như sau:

• Giá trị riêng (λ): Là các giá trị thỏa mãn phương trình (A – λI)x = 0, với x ≠ 0. Ma trận (A – λI) được gọi là ma trận đặc trưng của A.
• Vector riêng (v): Là các vectơ phi tầm thường thỏa mãn phương trình Av = λv. Mỗi giá trị riêng λ tương ứng với một tập con vectơ riêng chứa các vectơ v thỏa mãn Av = λv.
• Ma trận chéo là gì: Ma trận đường chéo B chứa các giá trị riêng của A trên đường chéo chính và các phần tử khác đều bằng 0.
• Ma trận chuyển đổi (T): Có các cột là các vector riêng tuyến tính độc lập của A.

Ma trận chéo hoá được khi nào?

Vậy ma trận chéo hoá được khi nào? Dưới đây là hai điều kiện cần và đủ để một ma trận chéo hoá được:

1. Ma trận khả nghịch

Điều kiện tiên quyết để một ma trận có thể chéo hóa được là nó phải khả nghịch. Nghĩa là, ma trận đó phải có ma trận nghịch đảo. Ký hiệu:

• A là ma trận cần chéo hóa.
• T là ma trận chuyển đổi.
• B là ma trận đường chéo chứa các giá trị riêng của A.

Công thức:

$$A=TBT^{-1}$$

Trong đó A là ma trận cần chéo hóa, T là ma trận chuyển đổi, và B là ma trận đường chéo chứa các giá trị riêng của A.

Ví dụ:

• Ma trận A = [[1, 2], [3, 4]] khả nghịch vì nó có ma trận nghịch đảo $$A^{-1}=\lbrack\lbrack-2,1\rbrack,\lbrack1,-1\rbrack\rbrack$$
• Ma trận B = [[1, 0], [0, 0]] không khả nghịch vì nó không có ma trận nghịch đảo.

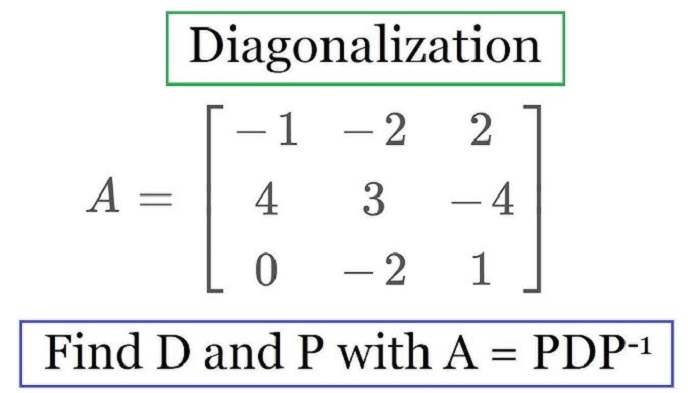
2. Tập con vectơ riêng đầy đủ

Ma trận A chỉ có thể chéo hóa được nếu mỗi giá trị riêng λ của A có tập con vectơ riêng đầy đủ.

Định nghĩa:

Tập con vectơ riêng đầy đủ: Là tập con vectơ chứa số vectơ riêng tuyến tính độc lập bằng độ đa thức tối tiểu của giá trị riêng λ.

Ví dụ:

• Ma trận A = [[1, 2], [3, 4]] có thể chéo hóa được vì mỗi giá trị riêng λ1 = 2 và λ2 = 5 đều có tập con vectơ riêng đầy đủ.
• Ma trận B = [[1, 0], [0, 0]] không thể chéo hóa được vì giá trị riêng λ = 0 chỉ có một vectơ riêng.

Các bước chéo hoá ma trận

Để giải các bài toán liên quan tới chéo hoá ma trận, bạn cần thực hiện theo 5 bước như sau:

+ Bước 1: Tìm giá trị riêng: Giải phương trình đặc trưng (A – λI)x = 0 để tìm các giá trị riêng λ.

+ Bước 2: Tìm vector riêng: Đối với mỗi giá trị riêng λ, giải phương trình Av = λv để tìm các vector riêng v tương ứng.

+ Bước 3: Xây dựng ma trận chuyển đổi: Sắp xếp các vector riêng tuyến tính độc lập thành các cột của ma trận T.

+ Bước 4: Xây dựng ma trận đường chéo: Đặt các giá trị riêng tìm được lên đường chéo chính của ma trận B.

+ Bước 5: Chéo hóa ma trận: Áp dụng công thức A = TBT^-1 để tìm ma trận chéo hóa.

Ví dụ minh hoạ về ma trận chéo

Để minh họa cho khái niệm chéo hóa ma trận, ta sẽ thực hiện chéo hóa ma trận A bằng cách tìm ma trận chuyển đổi T và ma trận đường chéo B.

Bước 1: Tìm giá trị riêng và vector riêng của ma trận A

Ma trận A (2×2): A =[2; 1; −1; 2]

• Xác định phương trình đặc trưng:(A−λI)x=0
• Giải phương trình đặc trưng:det(A−λI)=0(2−λ)(2−λ)+(−1)(1)=0(λ−2)2=0

Vậy, ma trận A có hai giá trị riêng trùng nhau λ = 2.

Tìm vector riêng tương ứng với giá trị riêng: λ = 2:(A−2I)x=0[01−10][x1x2]=[00]

Giải hệ phương trình, ta tìm được vector riêng v1 = [1, 1]T.

Vì giá trị riêng λ = 2 là giá trị riêng trùng nhau, ta cần tìm thêm một vector riêng nữa sao cho v1 và vector riêng mới v2 tuyến tính độc lập.

Ta có thể chọn v2 = [-1, 1]T.

Bước 2: Tạo ma trận chuyển đổi T

Ma trận chuyển đổi T được tạo thành từ các vector riêng v1 và v2 được sắp xếp thành cột:

P=[11−11]

Bước 3: Tạo ma trận đường chéo B

Ma trận đường chéo B chứa các giá trị riêng của A trên đường chéo chính và các phần tử khác đều bằng 0:

D=[2002]

Bước 4: Chéo hóa ma trận A

Sử dụng công thức chéo hóa ma trận:

A = TBT^−1

A=[11−11][2002][11−11]^-1

Tính toán, ta thu được:

A=[21−12]

Kết luận:

Qua ví dụ trên, ta đã thực hiện chéo hóa ma trận A thành ma trận đường chéo B bằng cách sử dụng ma trận chuyển đổi T. Ma trận B chứa các giá trị riêng của A, và T là ma trận được tạo thành từ các vector riêng của A.

Bài tập về chéo hoá ma trận

Để giúp bạn luyện tập và củng cố kiến thức giải bài tập về chéo hóa ma trận, chúng tôi đã tổng hợp một số bài tập với mức độ khó khác nhau.

Bài tập 1:

Chéo hóa ma trận A (2×2) = {1; 2; -2; 3}

Lời giải:

Tìm giá trị riêng và vector riêng của A:

Xác định phương trình đặc trưng: (A−λI)x=0

Giải phương trình đặc trưng: (λ−1)(λ−4)=0

Vậy, A có hai giá trị riêng λ1 = 1 và λ2 = 4.

Tìm vector riêng tương ứng với mỗi giá trị riêng:

λ1 = 1: (A – I)x = 0 ⇒ x = [2, -1]T

λ2 = 4: (A – 4I)x = 0 ⇒ x = [1, 2]T

Tạo ma trận chuyển đổi T: T=[2; −1; ​1; 2​]

Tạo ma trận đường chéo B: B=[1; 0;​ 0; 4​]

Chéo hóa ma trận A: A=TBT^−1=[2; −1; ​1; 2​][1; 0;​ 0; 4​][2; −1; ​1; 2​]^−1=[1; −2; ​2; 3​]

Bài tập 2:

Chứng minh rằng ma trận B là ma trận đường chéo:

B (3×3) =​{λ1;​ 0; 0; ​0; λ2; ​0; ​0; 0; λ3}

Chứng minh:

Ma trận B được gọi là ma trận đường chéo nếu tất cả các phần tử nằm ngoài đường chéo chính đều bằng 0.

Theo đề bài, B có dạng: B=​{λ1;​ 0; 0; ​0; λ2; ​0; ​0; 0; λ3}

Như ta thấy, tất cả các phần tử nằm ngoài đường chéo chính của B đều bằng 0. Do đó, B là ma trận đường chéo.

​​​Bài tập 3:

Cho ma trận A:

A (3×3) =​ {1;4;7;​2;5;8;​3;6;9}​​

Xác định xem ma trận A có thể chéo hóa được hay không. Nếu có, hãy tìm ma trận chuyển đổi P và ma trận đường chéo D để chéo hóa A.

Giải:

Xác định khả năng chéo hóa:

Tính định thức của ma trận A:det(A)=−3<0. Vậy, A khả nghịch.

Ma trận A có 3 giá trị riêng khác nhau (1, 2, 3).

Do đó, A có thể chéo hóa được.

Tìm ma trận chuyển đổi P và ma trận đường chéo D:

Tìm vector riêng tương ứng với mỗi giá trị riêng:

λ1​=1: v1​=[1,−1,1]T

λ2​=2: v2​=[2,1,−1]T

λ3​=3: v3​=[1,2,3]T

Tạo ma trận chuyển đổi T: T=​1−11​21−1​123​​

Tạo ma trận đường chéo B: B=​ {1;0;0;​0;2;0;​0;0;3}​​

Chéo hóa ma trận A theo công thức: A = TBT^−1

Lời kết

Nắm được những kiến thức nền tảng của chéo hóa ma trận sẽ giúp bạn khám phá thêm nhiều ứng dụng thú vị trong Đại số Tuyến tính và các lĩnh vực liên quan. Hãy kiên trì luyện tập và áp dụng kiến thức đã học để gặt hái thành công trong hành trình chinh phục tri thức của bạn.