Chu vi hình tam giác cân là công thức quan trọng trong toán học, nó không chỉ được sử dụng để giải quyết các bài toán mà còn ứng dụng thực tiễn rất nhiều. Cùng theo dõi bài viết dưới đây để tìm hiểu chi tiết phần kiến thức này.
Định nghĩa hình tam giác cân
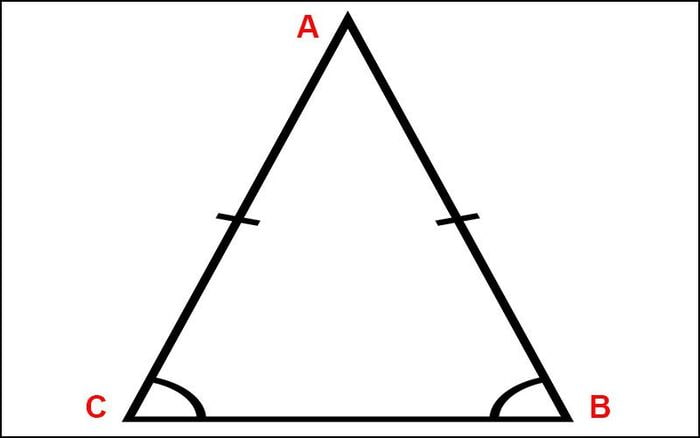
Hình tam giác cân là gì? Là tam giác sở hữu 2 cạnh bên bằng nhau, đỉnh của tam giác cân là giao điểm của hai cạnh bên. Góc được tạo nên từ hai cạnh bên là góc ở đỉnh, còn lại là 2 góc nhọn. Theo tính chất, 2 góc nhọn của tam giác cân bằng nhau.
Ví dụ minh họa:
Cho tam giác ABC cân tại A, suy ra:
- AB = AC
- góc ABC = góc ACB (tính chất 2 góc nhọn của tam giác cân)
- góc A là góc đỉnh
- góc ABC, góc ACB là 2 góc nhọn
Công thức tính chu vi hình tam giác cân
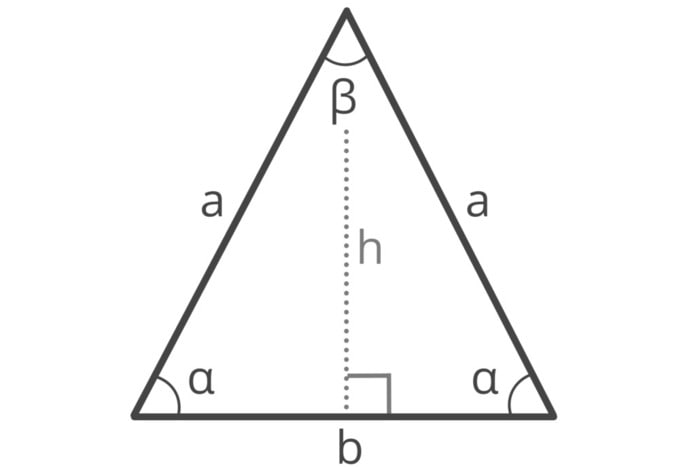
Để tính chu vi hình tam giác cân, chỉ cần biết độ dài các cạnh bên, cạnh đáy và áp dụng công thức đơn giản dưới đây. Công thức này được ứng dụng rất rộng rãi, không chỉ trong các dạng bài toán học mà còn giúp tính toán các vấn đề liên quan đến xây dựng và thiết kế kỹ thuật.
Công thức tính chu vi hình tam giác cân:
$$P\;=\;2a\;+\;b$$
Trong đó:
- a là độ dài của mỗi cạnh bên của tam giác cân.
- b là độ dài cạnh đáy của tam giác cân.
Ví dụ minh họa:
Cho một tam giác cân OAB cân tại O, ta có OA = OB = 5 cm và AB = 7 cm. Tính chu vi tgc OAB.
Hướng dẫn giải: Chu vi tam giác cân OAB là: $$P\;=\;2\;\times\;5\;+\;7\;=\;17\;cm$$
Xem thêm: Đường cao tam giác cân là một thông số quan trọng
Một số bài toán về chu vi tgc
Dưới đây là một số bài toán áp dụng cách tính chu vi hình tam giác cân:
Bài tập minh họa 1: Cho tam giác ABC cân tại A, biết AB = AC = 7 cm và BC = 9 cm. Tính chu vi tam giác cân ABC.
Hướng dẫn giải:
Áp dụng công thức tính chu vi hình tam giác cân, ta có: $$P(ABC)\;=\;2\times7+9\;=\;23\;cm$$
Vậy chu vi tam giác ABC là 23 cm.
Bài tập minh họa 2: Cho tam giác OAB cân tại O, biết OA = OB = 8 cm và chu vi tam giác OAB là 21 cm. Tính cạnh đáy AB?
Hướng dẫn giải:
Áp dụng công thức ta được, $$P(OAB)\;=\;2\times OA+AB\;=>\;AB\;=\;P(OAB)-2\times OA\;=\;21\;-\;2\;\times\;8\;=\;5\;cm.$$
Vậy cạnh đáy AB là 5 cm.
Bài tập minh họa 3: Cho tam giác OXY cân tại O, biết cạnh đáy XY là 7 cm và chu vi tam giác OXY là 27 cm. Tính 2 cạnh bên OX và OY?
Hướng dẫn giải:
Áp dụng công thức ta được, $$P(OXY)\;=\;2\times OX+XY\;=>\;OX\;=\frac{(P\;-\;XY)}2=\;\frac{\displaystyle(27\;-\;7)}{\displaystyle2}\;=\;10\;cm$$
Vậy 2 cạnh bên OX = OY = 10 cm.
Bài tập minh họa 4:
Cho tam giác cân CDE với CD = CE và độ dài cạnh đáy DE = 6 cm. Biết rằng chiều cao từ đỉnh C xuống DE là 4 cm. Tính chu vi của tam giác cân này.
Hướng dẫn giải:
*) Tính độ dài cạnh bên CD = CE:
Do tam giác cân CDE cân tại C, đường cao CX cũng là đường trung tuyến. Do đó, X là trung điểm của DE, tức DX = XE = DE/2 = 6/2 = 3 cm.
Xét tam giác vuông CDX với CX = 4 cm và DX = 3 cm, ta có:
$$CD=\surd(CX^2+DX^2)=\surd(4^2+3^2)=\surd(16+9)=5cm.$$
*) Tính chu vi tam giác CDE là tổng độ dài 3 cạnh:
$$P\;=\;5\;+\;5\;+\;6\;=\;16\;cm.$$
Tham khảo thêm: Cách chứng minh tam giác cân nhanh chóng và chuẩn xác
Lưu ý cần biết khi tính chu vi
Khi tính chu vi hình tam giác, các bạn cần lưu ý một số lỗi thường mắc phải như sau:
- Sử dụng đúng công thức: Cần áp dụng đúng công thức P = 2a + b. Nhiều trường hợp sử dụng sai công thức, đặc biệt các bài toán phức tạp, bạn cần xác định chuẩn xác độ dài của cạnh bên và cạnh đáy.
- Sai trong quá trình đo độ dài: Cần lưu ý đo chuẩn xác độ dài các cạnh, sử dụng công cụ chất lượng giúp đảm bảo kết quả chuẩn xác.
- Cần xác định chuẩn xác góc tại đỉnh, góc nhọn để đảm bảo đây là một hình tam giác cân. Công thức tính trên chỉ đúng khi đây là tam giác cân.
- Đặc biệt, những bài toán cho số đo của các cạnh khác đơn vị đo thì cần đổi lại cho trùng khớp.
Có thể bạn quan tâm: Những DHNB hình tam giác cân mà bạn cần biết
Ứng dụng của chu vi tam giác cân trong thực tiễn
Không chỉ được sử dụng trong lĩnh vực toán học mà công thức tính tam giác cân còn được ứng dụng phổ biến trong thực tiễn, như sau:
- Kiến trúc và xây dựng: Các kỹ sư, nhà thiết kế ứng dụng công thức chu vi để tính toán, đo đạc kết cấu cho các công trình như cầu, mái vòm và các thiết kế yêu cầu độ đối xứng và cân bằng.
- Thiết kế sản phẩm: Trong thiết kế công nghiệp, việc nắm được công thức chi vi giúp tiết kiệm không gian trong sản xuất các dụng cụ, bộ phận máy móc hay đồ gia dụng.
- Trang trí và nghệ thuật: chu vi tam giác cân còn ảnh hưởng đến sự cân bằng thẩm mỹ của tác phẩm, từ điêu khắc đến trang trí nội thất.
- Nghiên cứu và giáo dục: công thức này được sử dụng để tính toán ở nhiều dạng bài khác nhau, chúng xuất hiện xuyên suốt quá trình học tập trên ghế nhà trường.

Tính chu vi hình tam giác cân là kiến thức học thuật quan trọng mà các bạn cần nắm vững. Chúng được áp dụng không chỉ trong các bài toán học, mà còn được ứng dụng thực tiễn rất nhiều như kiến trúc, thiết kế, trang trí, nghệ thuật và giáo dục.




