Chu vi hình thang là một khái niệm quan trọng trong hình học và có ứng dụng rộng rãi trong thực tế. Việc tính CV không chỉ giúp chúng ta hiểu rõ hơn về cấu trúc của hình thang mà còn áp dụng vào các vấn đề đo lường và thiết kế trong cuộc sống hàng ngày. Trong bài viết này, hãy cùng chúng tôi tìm hiểu công thức tính chu vi ht và những ứng dụng của nó trong các tình huống thực tế!
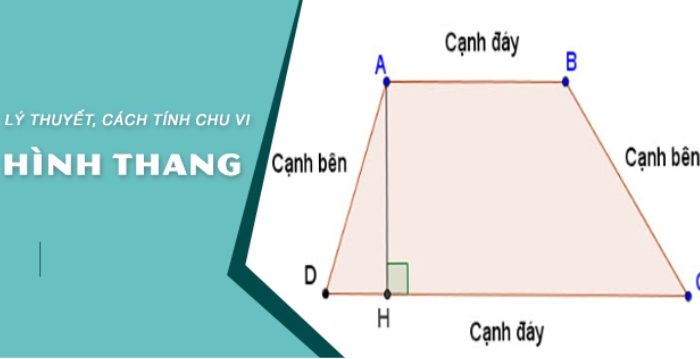
Công thức tính chu vi hình thang
Chu vi hình thang được tính bằng công thức:
$$Chu\;vi\;ht\;=\;a\;+\;b\;+\;c\;+\;d$$
Diễn đạt bằng lời: CV hình thang bằng tổng độ dài của các cạnh cộng lại với nhau.
Ví dụ:
Nếu đề cho hình thang ABCD với các cạnh cho sẵn: AB = 4, CD = 6, AD = 3, và BC = 7, để tính chu vi hình ABCD, bạn cộng tổng độ dài của các cạnh lại với nhau:
Chu vi = AB + CD + AD + BC = 4 + 6 + 3 + 7 = 20.

Đọc ngay: Hình thang là gì? Cách tính diện tích, CV của hình thang
Các bước tính chu vi hình thang
Để tính CV của một hình thang bất kỳ, bạn cần làm theo các bước sau:
- Bước 1: Xác định độ dài các cạnh của hình thang. Đặt hai cạnh bên là (c, d) hai cạnh đáy là (a, b)
- Bước 2: Tính tổng độ dài của các cạnh bằng cách sử dụng công thức chu vi ht = a + b + c + d. Trong đó, a, b, c, d là giá trị độ dài của các cạnh tương ứng.
- Bước 3: Thực hiện phép tính để có kết quả CV của hình thang.
Ví dụ hướng dẫn:
Đề bài: Cho hình thang ABCD có các cạnh như sau: AB = 5 cm, CD = 7 cm, AD = 4 cm, và BC = 8 cm. Tính chu vi ht ABCD?
Các bước làm
- Bước 1: Xác định độ dài 2 cạnh đáy: a = 5, b = 7; độ dài 2 cạnh bên c = 4, d = 8
- Bước 2: Tính tổng độ dài các cạnh: a + b + c + d = 5 + 7 + 4 + 8.
- Bước 3: Kết quả chu vi ht ABCD là 24 cm.

Tham khảo thêm: Các cách chứng minh hình thang chi tiết
Một số dạng bài tập minh hoạ
Dạng bài cho đáy lớn, đáy nhỏ và chiều cao, chưa có 2 cạnh bên:
VD: Cho hình thang với đáy lớn là a, đáy nhỏ là b và chiều cao là h. Yêu cầu tính chu vi ht.
Hướng dẫn thực hiện
Bước 1: Xác định độ dài các cạnh: Gọi a là đáy lớn, b là đáy nhỏ, và h là chiều cao.
Bước 2: Tính tổng độ dài 4 cạnh của hình thang:
- Cạnh đáy lớn: a
- Cạnh đáy nhỏ: b
- Hai cạnh bên: c và c (các cạnh này có độ dài giống nhau)
Cạnh bên áp dụng công thức Pythagore để tính:
$$h^2+{(\frac{a-b}2)}^2\\$$
Bước 3: Tính tổng độ dài 4 cạnh.
Bước 4: Kết quả của tổng độ dài 4 cạnh chính là chu vi của ht đề cho.
Bài tập mẫu: Cho hình thang ABCD với đáy lớn a = 6 cm, đáy nhỏ b = 4 cm và chiều cao h = 3 cm. Yêu cầu tính CV hình thang.
Giải
Bước 1: a = 6 cm, b = 4 cm, h = 3 cm
Bước 2: Tính cạnh bên:
$$c=3^2+{(\frac{6-4}2)}^2=\;9\;+\;1\;=\;10$$
Bước 3: Tính tổng độ dài 4 cạnh:
Tổng a + b + c + c = 6 + 4 + 10 + 10 = 10 + 210
Bước 4: Chu vi ht là 10 + 210 cm
Xem ngay: Có các dấu hiệu hình thang nào? Các bài tập mẫu vận dụng
Ứng dụng của chu vi hình thang trong thực tế
Tính chu vi ht không chỉ là một khái niệm trong sách giáo khoa mà còn có ứng dụng rất rộng rãi trong cuộc sống hàng ngày và trong nhiều lĩnh vực khác nhau:
- Trong học tập, việc tính chu vi hình giúp chúng ta áp dụng kiến thức toán học vào thực tiễn. Khi làm các bài tập về hình học, việc này giúp chúng ta hiểu rõ hơn về cấu trúc và tính chất của hình thang, từ đó áp dụng vào việc giải quyết các bài toán phức tạp hơn. Ví dụ như việc tính chu vi của sân bóng đá, hồ bơi, hoặc diện tích một khu đất trong môn địa lý.
- Trong cuộc sống hàng ngày, việc tính chu vi hình thang cũng rất hữu ích. Nếu muốn xây dựng hoặc thiết kế một không gian mới trong nhà, bạn cần tính toán kích thước và chu vi của các hình này để chọn được loại vật liệu phù hợp cũng như ước tính được chi phí. Như vậy, việc áp dụng công thức tính cv ht đặc biệt quan trọng trong lĩnh vực kiến trúc, xây dựng, và quy hoạch đô thị.
Đọc ngay: Đường chéo hình thang là gì? Công thức tính và hướng dẫn giải bài tập mẫu
Hy vọng bài viết đã giúp bạn nắm được công thức tính chu vi hình thang cũng như biết cách vận dụng để giải các bài toán cơ bản. Đừng quên theo dõi các bài viết khác của Học Thế Nào để có thêm nhiều kiến thức toán học bổ ích khác nhé!