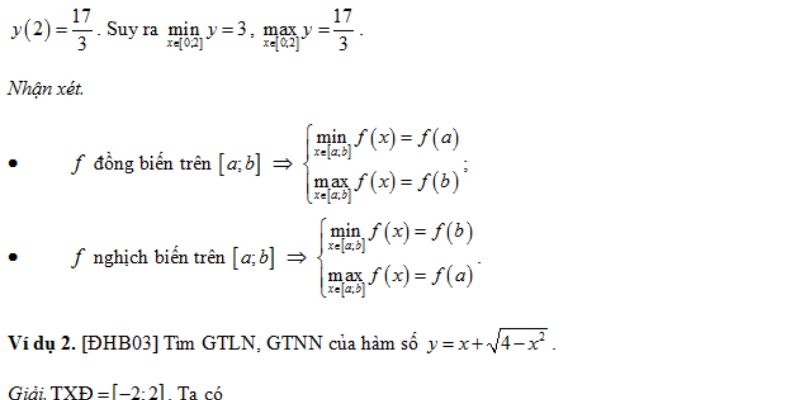Tìm giá trị lớn nhất nhỏ nhất của hàm số và các phương pháp hiệu quả nhất

Tìm giá trị lớn nhất nhỏ nhất của hàm số là một vấn đề cơ bản trong giải tích, giúp xác định các cực trị quan trọng của hàm. Kỹ năng này không chỉ hỗ trợ trong giải bài toán mà còn có ứng dụng rất lớn trong nhiều lĩnh vực. Hãy cùng khám phá các phương pháp và quy trình để tìm ra giá trị lớn nhất và nhỏ nhất của hàm số một cách hiệu quả.

Tìm giá trị lớn nhất nhỏ nhất của hàm số là gì và tại sao cần tìm?

Tìm giá trị lớn nhất nhỏ nhất của hàm số là quá trình xác định các điểm cực trị của hàm số, từ đó tìm ra giá trị lớn nhất và nhỏ nhất mà hàm số có thể đạt được trong một khoảng xác định. Đây là một phần quan trọng trong lý thuyết giải tích và có nhiều ứng dụng thực tiễn.

Việc tìm cực trị giúp ta hiểu được đặc điểm và quy luật biến thiên của hàm số. Trong thực tế, các bài toán tối ưu hóa thường yêu cầu tìm giá trị tốt nhất (lớn nhất hoặc nhỏ nhất) của một đại lượng nào đó. Ví dụ như tìm chi phí sản xuất thấp nhất, lợi nhuận cao nhất hay diện tích lớn nhất.

Ngoài ra, việc xác định cực trị còn giúp ta dự đoán và kiểm soát được các trường hợp giới hạn của hệ thống. Trong kỹ thuật, việc biết được giá trị lớn nhất và nhỏ nhất mà một hệ thống có thể đạt tới giúp đảm bảo an toàn và hiệu quả trong vận hành. Chẳng hạn như xác định tải trọng tối đa của cầu, áp suất tối đa của bình chứa hay nhiệt độ giới hạn của thiết bị.

Các phương pháp cơ bản để xác định giá trị lớn nhất và nhỏ nhất của hàm số

Cách tìm giá trị lớn nhất nhỏ nhất của hàm số thường được thực hiện thông qua 3 phương pháp chính: dùng đạo hàm tìm cực trị, khảo sát dấu đạo hàm và sử dụng bất đẳng thức. Mỗi phương pháp có những ưu điểm và phạm vi áp dụng riêng, giúp xác định chính xác giá trị lớn nhất và giá trị nhỏ nhất của hàm số trong từng trường hợp cụ thể.

Phương pháp dùng đạo hàm để tìm cực trị

Phương pháp này dựa trên việc tìm các điểm cực trị của hàm số bằng cách giải phương trình đạo hàm bằng 0. Khi đã xác định được các điểm cực trị, ta so sánh giá trị hàm số tại các điểm này với giá trị tại biên để tìm ra giá trị lớn nhất và nhỏ nhất.

Phương pháp này đặc biệt hiệu quả với các hàm số liên tục trên khoảng xác định và có đạo hàm. Ví dụ như hàm bậc 2, bậc 3 hay các hàm đa thức, việc tìm đạo hàm và giải phương trình đạo hàm sẽ cho ta cái nhìn tổng quan về sự biến thiên của hàm số.

Phương pháp khảo sát dấu của đạo hàm

Việc khảo sát dấu của đạo hàm giúp ta xác định được các khoảng đơn điệu tăng giảm của hàm số. Khi đạo hàm dương, hàm số tăng. Ngược lại khi đạo hàm âm, hàm số giảm.

Bằng cách lập bảng biến thiên và xét dấu đạo hàm tại các điểm và khoảng, ta có thể xác định được xu hướng biến thiên của hàm số. Điều này giúp ta dễ dàng nhận biết vị trí đạt giá trị lớn nhất và nhỏ nhất của hàm số trên tập xác định.

Phương pháp dùng bất đẳng thức

Phương pháp này thường áp dụng cho các bài toán đặc biệt, khi ta có thể biến đổi biểu thức của hàm số thành dạng bất đẳng thức quen thuộc như Cauchy, Bunhiacopxki hay bất đẳng thức giữa trung bình cộng và trung bình nhân.

Ưu điểm của phương pháp này là có thể tìm được giá trị lớn nhất hoặc nhỏ nhất mà không cần phải tính đạo hàm. Tuy nhiên, việc áp dụng đòi hỏi kinh nghiệm trong việc nhận dạng và biến đổi biểu thức phù hợp với các dạng bất đẳng thức chuẩn.

Các bước chi tiết tìm giá trị lớn nhất của hàm số

Để tìm được giá trị lớn nhất của một hàm số, cần thực hiện quy trình phân tích có hệ thống. Quá trình này giúp xác định chính xác các điểm có khả năng đạt giá trị lớn nhất và so sánh chúng một cách logic. Việc tìm giá trị lớn nhất của hàm số đòi hỏi sự tỉ mỉ và tuân thủ các bước cơ bản.

Xác định tập xác định của hàm số

Bước đầu tiên là xác định chính xác miền xác định của hàm số. tìm tập xác định của hàm số 12 sẽ giúp giới hạn phạm vi cần khảo sát. Việc này giúp tránh bỏ sót các điểm quan trọng có thể chứa giá trị cực đại.

Khi xác định tập xác định, cần chú ý đến các điều kiện đặc biệt như mẫu số khác 0, biểu thức dưới dấu căn không âm. Điều này đảm bảo tính chính xác của kết quả cuối cùng.

Tìm các điểm cực trị và giá trị bất thường

Sau khi có tập xác định, tiến hành tìm các điểm cực trị bằng phương pháp đạo hàm. cách tìm giá trị bất thường cũng rất quan trọng vì chúng có thể chứa giá trị lớn nhất của hàm số.

Các điểm cần xét bao gồm:

• Điểm có đạo hàm bằng 0
• Điểm không tồn tại đạo hàm
• Các điểm đầu mút của khoảng xác định
• Các điểm gián đoạn của hàm số

So sánh các giá trị để tìm GTLN

Sau khi có danh sách các điểm cần khảo sát, thay từng giá trị vào hàm số ban đầu để tính giá trị hàm. Việc so sánh cần được thực hiện một cách có hệ thống và ghi chép cẩn thận để tránh nhầm lẫn.

Giá trị lớn nhất sẽ là giá trị lớn nhất trong tất cả các giá trị đã tính được. Cần kiểm tra lại kết quả bằng cách vẽ đồ thị hoặc xét dấu đạo hàm để đảm bảo không bỏ sót điểm nào.

Quy trình xác định giá trị nhỏ nhất của hàm số

Để tìm giá trị nhỏ nhất của hàm số, cần thực hiện một quy trình gồm 3 bước chính: xác định điểm cực tiểu, xét giá trị tại biên và so sánh các giá trị để tìm ra giá trị nhỏ nhất của hàm số. Mỗi bước đều đóng vai trò quan trọng trong việc xác định chính xác kết quả.

Tìm các điểm cực tiểu

Bước đầu tiên là tìm các điểm cực tiểu bằng cách khảo sát đạo hàm của hàm số. Khi đạo hàm bằng 0 hoặc không tồn tại, ta sẽ có các điểm tới hạn tiềm năng.

Sau khi có các điểm tới hạn, cần kiểm tra đạo hàm cấp 2 để xác định điểm nào là cực tiểu. Nếu đạo hàm cấp 2 dương tại một điểm, điểm đó chính là cực tiểu. Như giá trị cực đại là x hay y đã đề cập, việc phân biệt cực đại và cực tiểu rất quan trọng trong quá trình này.

Xét giá trị tại biên

Việc xét giá trị tại biên là bước không thể bỏ qua trong quá trình tìm giá trị nhỏ nhất. Tại các điểm biên của miền xác định, hàm số có thể đạt giá trị nhỏ hơn các điểm cực tiểu bên trong.

Với hàm số có miền xác định là khoảng hữu hạn [a,b], cần tính giá trị hàm số tại a và b. Đối với miền vô hạn, cần xét giới hạn của hàm số khi x tiến đến dương vô cực và âm vô cực.

So sánh để tìm GTNN

Sau khi có đầy đủ các giá trị cần thiết, bước cuối cùng là so sánh chúng với nhau. Các giá trị cần đưa vào so sánh bao gồm giá trị tại các điểm cực tiểu và giá trị tại các điểm biên.

Giá trị nhỏ nhất trong tất cả các giá trị đã tìm được chính là cách tính giá trị nhỏ nhất của hàm số. Kết quả này sẽ cho ta biết điểm nào trên đồ thị hàm số có tọa độ y thấp nhất.

Ví dụ minh họa và bài tập áp dụng tìm GTLN-GTNN

Việc tìm giá trị lớn nhất nhỏ nhất của hàm số đòi hỏi sự thành thạo trong việc áp dụng các phương pháp khác nhau. Để nắm vững kỹ năng này, ta cần xem xét các ví dụ cụ thể và thực hành qua các bài tập đa dạng.

Trước khi đi vào chi tiết các ví dụ, cần lưu ý rằng việc xác định giới hạn của hàm số là bước quan trọng giúp ta xác định chính xác các điểm cực trị. Điều này sẽ được minh họa rõ qua các ví dụ sau.

Ví dụ với hàm bậc 2

Xét hàm số f(x) = -x² + 4x – 3 trên R. Để tìm GTLN-GTNN, ta thực hiện các bước sau:

Bước 1: Tìm đạo hàm f'(x) = -2x + 4
Bước 2: Giải f'(x) = 0 => x = 2
Bước 3: Kiểm tra dấu f'(x):

• Khi x < 2: f'(x) > 0, hàm số tăng
• Khi x > 2: f'(x) < 0, hàm số giảm

Do đó tại x = 2, hàm số đạt GTLN = 1.

Ví dụ với hàm mũ và logarit

Xét hàm số g(x) = ln(x) – x + 2 trên (0,+∞). Đây là một ví dụ điển hình về GTLN GTNN của hàm số có chứa logarit.

Tìm đạo hàm: g'(x) = 1/x – 1
Giải g'(x) = 0 => x = 1

Kiểm tra biến thiên cho thấy:

• Khi 0 < x < 1: g'(x) > 0, hàm số tăng
• Khi x > 1: g'(x) < 0, hàm số giảm

Vậy tại x = 1, hàm số đạt GTLN = 1.

Bài tập tự luyện có lời giải

Để giúp người học nắm vững phương pháp, ta giải quyết bài tập sau từ Học Thế Nào:

Tìm GTLN-GTNN của hàm số h(x) = x³ – 3x² trên [-1,2]

Lời giải:

• Tìm đạo hàm: h'(x) = 3x² – 6x
• Giải h'(x) = 0 => x(3x – 6) = 0 => x = 0 hoặc x = 2
• Lập bảng biến thiên và so sánh giá trị tại:
• x = -1: h(-1) = -1 + 3 = 2
• x = 0: h(0) = 0
• x = 2: h(2) = 8 – 12 = -4

Kết luận: GTLN = 2 tại x = -1, GTNN = -4 tại x = 2.

Trong toán học, việc tìm giá trị lớn nhất nhỏ nhất của hàm số đóng vai trò quan trọng trong việc phân tích và hiểu rõ tính chất của các hàm. Bài viết đã trình bày các phương pháp xác định giá trị cực trị, từ việc sử dụng đạo hàm đến khảo sát dấu đạo hàm, giúp người học dễ dàng áp dụng vào các bài toán cụ thể. Nắm vững kiến thức này sẽ hỗ trợ học sinh trong quá trình giải quyết các bài tập liên quan đến hàm số hiệu quả hơn.