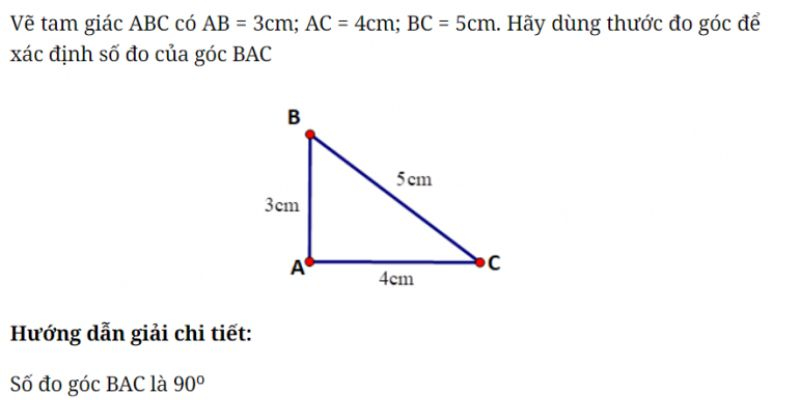
Định lý Pytago: Công thức, chứng minh và ứng dụng trong giải toán dễ hiểu

Định lý Pytago là một trong những kiến thức căn bản quan trọng trong hình học. Bài viết này bàn luận về phát biểu và chứng minh định lý này, cũng như công thức và ứng dụng trong giải toán. Đặc biệt, bạn sẽ khám phá mối liên hệ giữa định lý Pytago và các lĩnh vực khác trong toán học, từ đó nâng cao kỹ năng tư duy và giải quyết bài toán.

Định lý Pytago và ý nghĩa trong hình học

Định lý Pytago là một trong những định lý quan trọng nhất trong hình học, phát biểu rằng trong tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh góc vuông. Công thức toán học của định lý được biểu diễn là a² + b² = c², trong đó c là cạnh huyền, a và b là hai cạnh góc vuông.

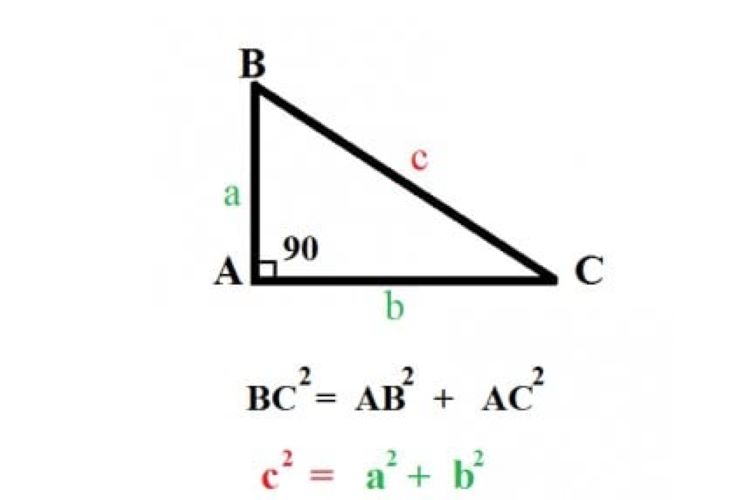
Ý nghĩa của định lý pythagore thể hiện rõ nét trong việc tính toán khoảng cách và độ dài trong không gian hai chiều. Định lý giúp xác định chính xác độ dài cạnh còn lại của tam giác vuông khi biết hai cạnh, đồng thời cũng là công cụ để kiểm tra một tam giác có phải là tam giác vuông hay không.

Trong thực tế, định lý được ứng dụng rộng rãi trong nhiều lĩnh vực như xây dựng, kiến trúc và đo đạc. Ví dụ, khi cần đo chiều cao của một tòa nhà cao tầng, người ta có thể sử dụng định lý này bằng cách đo khoảng cách từ điểm quan sát đến chân tòa nhà và góc ngẩng từ mắt người quan sát đến đỉnh tòa nhà.

Ngoài ra, định lý còn là nền tảng cho nhiều phát triển quan trọng trong toán học hiện đại như hình học giải tích, lượng giác và vector. Các ứng dụng của định lý trong công nghệ định vị GPS, thiết kế game 3D hay tính toán quỹ đạo vệ tinh đều dựa trên nguyên lý cơ bản này.

Phát biểu và chứng minh định lý Pytago trong tam giác vuông

Định lý Pytago là một trong những định lý quan trọng nhất trong hình học. Định lý này được phát hiện bởi nhà toán học Pythagoras người Hy Lạp cổ đại và có ứng dụng rộng rãi trong nhiều lĩnh vực. Theo Học Thế Nào VN, đây là một trong những định lý cơ bản nhất mà học sinh cần nắm vững.

Định lý pitago đã được chứng minh bằng nhiều phương pháp khác nhau, trong đó phổ biến nhất là phương pháp diện tích và phương pháp đại số. Mỗi phương pháp đều có những ưu điểm riêng giúp người học hiểu sâu hơn về bản chất của định lý.

Phát biểu định lý Pytago

Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Nếu gọi a, b là độ dài hai cạnh góc vuông và c là độ dài cạnh huyền, ta có Pytago công thức: c² = a² + b².

Định lý này áp dụng cho mọi tam giác vuông, không phụ thuộc vào kích thước hay tỷ lệ các cạnh. Điều kiện duy nhất là tam giác phải có một góc vuông 90 độ.

Chứng minh định lý Pytago bằng phương pháp diện tích

Phương pháp diện tích sử dụng việc so sánh diện tích các hình vuông và tam giác để chứng minh định lý. Ta vẽ hình vuông cạnh (a+b) và chia thành các phần như sau:

Một hình vuông lớn có cạnh (a+b) chứa bốn tam giác vuông bằng nhau và một hình vuông nhỏ ở giữa. Các tam giác này có các cạnh góc vuông là a và b, cạnh huyền là c.

Diện tích hình vuông lớn có thể tính theo hai cách:

• Cách 1: S = (a+b)²
• Cách 2: S = c² + 4(ab/2) = c² + 2ab

Chứng minh định lý Pytago bằng phương pháp đại số

Phương pháp đại số sử dụng các phép biến đổi toán học để chứng minh định lý. Xuất phát từ đẳng thức (a+b)² = (a+b)(a+b).

Ta có thể khai triển:
(a+b)² = a² + 2ab + b²

Từ kết quả chứng minh bằng phương pháp diện tích, ta đã có:
(a+b)² = c² + 2ab

Do đó: a² + 2ab + b² = c² + 2ab
Rút gọn: a² + b² = c²

Đây chính là công thức của định lý Pytago mà ta cần chứng minh.

Công thức định lý Pytago và cách áp dụng trong giải toán

Công thức định lý Pytago là một trong những công thức quan trọng nhất trong hình học, được sử dụng rộng rãi để tính toán độ dài các cạnh trong tam giác vuông. Công thức này có mối liên hệ mật thiết với lượng giác toán và được ứng dụng trong nhiều bài toán thực tế.

Để áp dụng hiệu quả định lý này, cần nắm vững công thức cơ bản và các dạng bài tập thường gặp. Việc thực hành giải nhiều bài tập đa dạng sẽ giúp củng cố kiến thức và phát triển kỹ năng vận dụng công thức một cách linh hoạt.

Công thức cơ bản của định lý Pytago

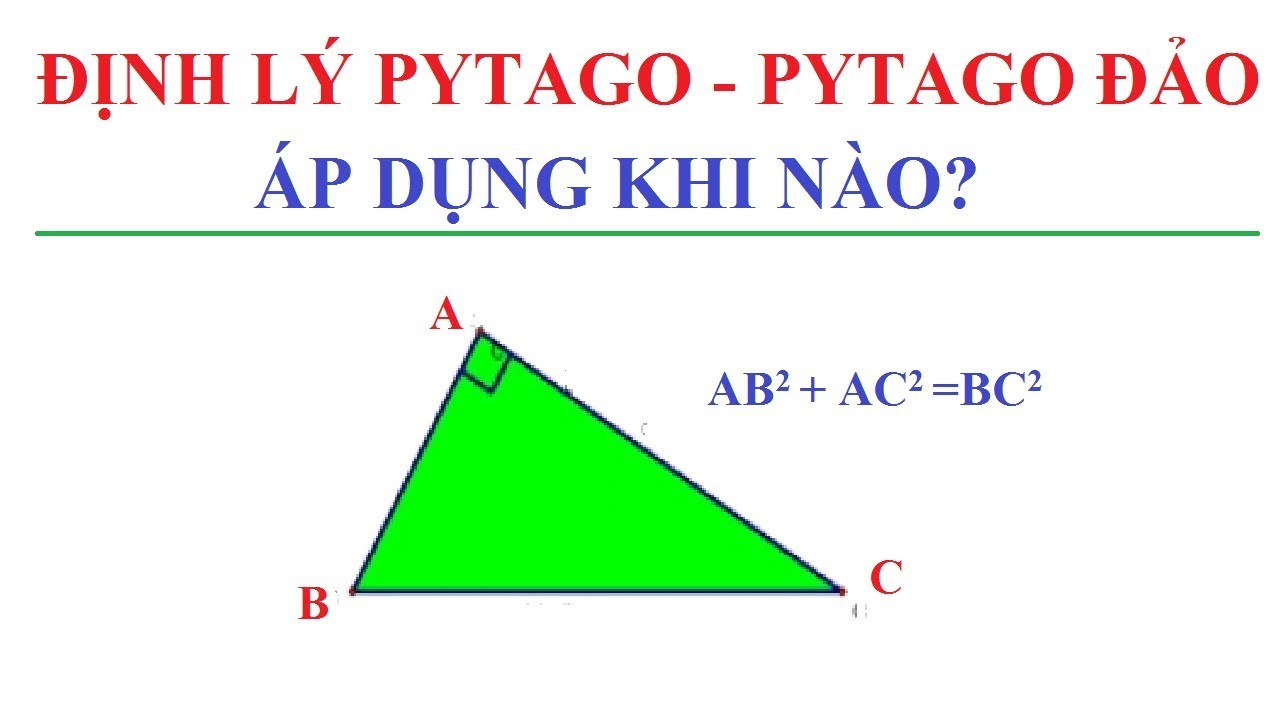
Trong tam giác vuông ABC vuông tại A, công thức pythagoras phát biểu rằng bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Công thức được viết dưới dạng: BC² = AB² + AC².

Công thức này áp dụng cho mọi tam giác vuông, không phụ thuộc vào kích thước hay tỷ lệ các cạnh. Điều kiện duy nhất là tam giác phải có một góc vuông 90 độ.

Ngoài ra, công thức còn có thể viết dưới dạng tổng quát: a² = b² + c², trong đó a là cạnh huyền, b và c là hai cạnh góc vuông của tam giác.

Các dạng bài tập thường gặp

Bài toán tìm cạnh huyền khi biết hai cạnh góc vuông là dạng cơ bản nhất. Đây là ứng dụng trực tiếp của định lý pythagoras trong việc tính toán độ dài cạnh còn thiếu.

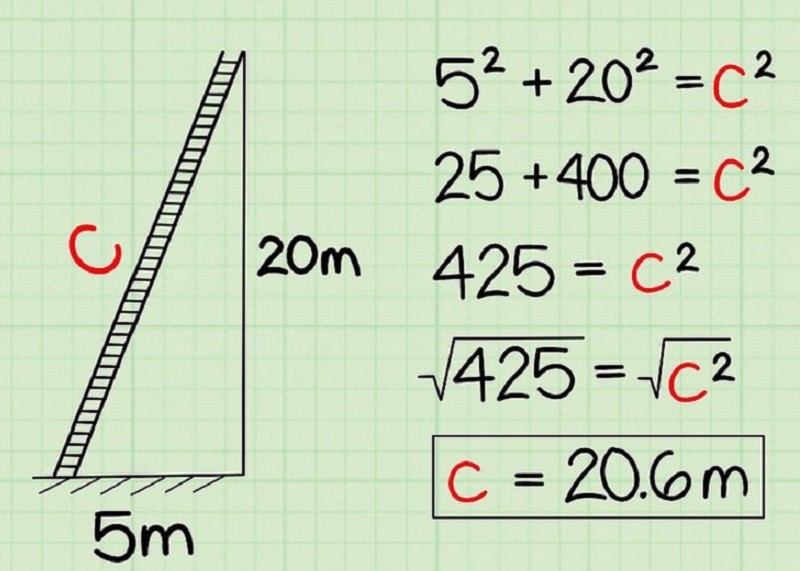
Dạng bài tập nâng cao thường yêu cầu tìm độ dài đường cao, đường trung tuyến hoặc các đoạn thẳng đặc biệt khác trong tam giác vuông. Những bài toán này đòi hỏi khả năng phân tích và kết hợp nhiều kiến thức hình học.

Một số bài tập ứng dụng thực tế như tính khoảng cách, độ cao tòa nhà hay độ dài cầu thang cũng thường xuyên xuất hiện và có ý nghĩa thực tiễn cao.

Phương pháp giải bài tập áp dụng định lý Pytago

Bước đầu tiên khi giải bài tập là xác định tam giác vuông trong bài toán. Nhiều khi tam giác vuông không được cho trực tiếp mà cần phải chứng minh hoặc tạo ra từ các yếu tố cho trước.

Sau khi xác định được tam giác vuông, cần phân tích kỹ các yếu tố đã biết và cần tìm. Việc vẽ hình chính xác, ghi rõ các số đo đã cho sẽ giúp quá trình giải toán trở nên dễ dàng hơn.

Cuối cùng, áp dụng công thức phù hợp và thực hiện các phép tính một cách cẩn thận. Trong nhiều trường hợp, có thể cần kết hợp định lý Pytago với các định lý khác để giải quyết bài toán hoàn chỉnh.

Định lý Pytago đảo và ứng dụng trong kiểm tra tam giác vuông

Định lý Pytago đảo là một phần quan trọng trong hình học, giúp kiểm tra một tam giác có phải là tam giác vuông hay không dựa trên độ dài các cạnh. Định lý này có mối liên hệ chặt chẽ với định lý Pytago cơ bản và được ứng dụng rộng rãi trong thực tế.

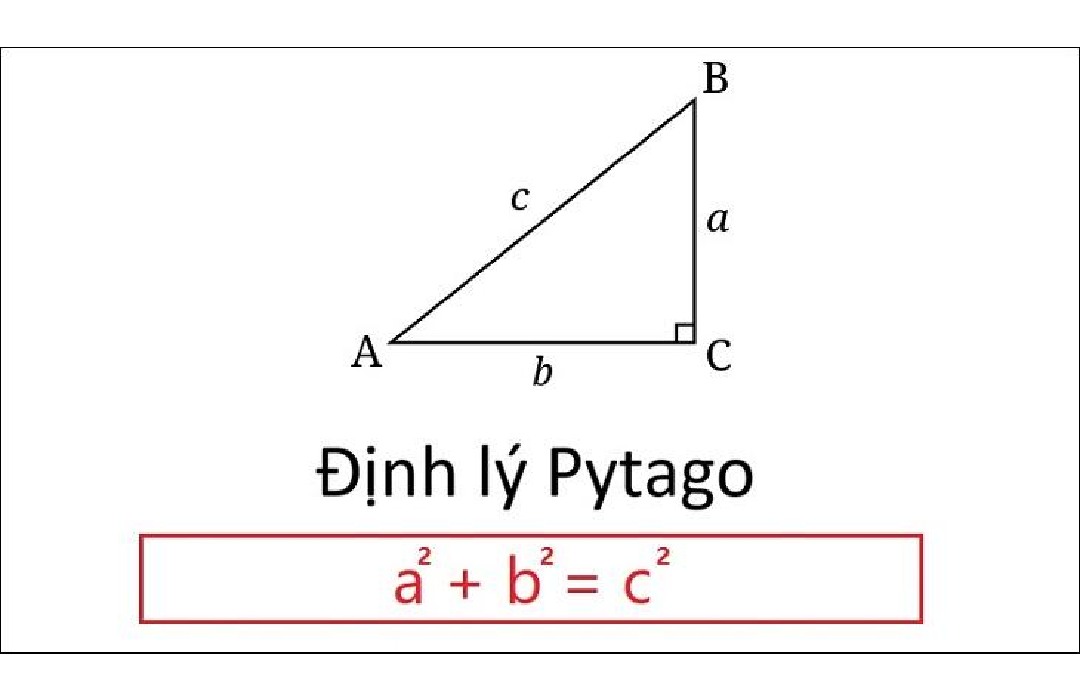
Phát biểu định lý Pytago đảo

Định lý Pytago đảo phát biểu rằng: Trong một tam giác, nếu bình phương độ dài cạnh lớn nhất bằng tổng bình phương độ dài hai cạnh còn lại thì tam giác đó là tam giác vuông. Nói cách khác, với tam giác ABC có c là cạnh dài nhất, nếu c² = a² + b² thì tam giác ABC là tam giác vuông tại đỉnh đối diện với cạnh c.

Định lý này có ý nghĩa quan trọng vì nó cung cấp một điều kiện đủ để xác định một tam giác là tam giác vuông mà không cần đo góc trực tiếp. Công thức định lý pytago đảo giúp giải quyết nhiều bài toán thực tiễn trong xây dựng và thiết kế.

Chứng minh định lý Pytago đảo

Để chứng minh định lý này, ta sử dụng phương pháp phản chứng. Giả sử tam giác ABC có c² = a² + b² nhưng không vuông tại A. Khi đó, ta có thể dựng một tam giác vuông A’BC sao cho BC = c và BA’ = a.

Theo định lý Pytago trong tam giác vuông A’BC:
c² = a² + (CA’)²

So sánh với giả thiết ban đầu:
c² = a² + b²

Do đó: (CA’)² = b²
Suy ra: CA’ = b = CA

Điều này chứng tỏ điểm A trùng với A’, nghĩa là tam giác ABC vuông tại A.

Ứng dụng trong bài toán kiểm tra tam giác vuông

Pytago đảo được áp dụng rộng rãi trong việc kiểm tra tam giác vuông. Trong thực tế xây dựng, thợ xây thường sử dụng nguyên lý này để kiểm tra độ vuông góc của các bức tường.

Một ví dụ điển hình là phương pháp 3-4-5: Nếu ba cạnh của một tam giác có tỷ lệ 3:4:5 (hay các bội số của chúng như 6:8:10, 9:12:15), tam giác đó chắc chắn là tam giác vuông. Điều này được áp dụng phổ biến trong công tác đo đạc và xây dựng nhà ở.

Ngoài ra, công thức định lý pytago đảo còn được ứng dụng trong thiết kế các công trình kiến trúc, đặc biệt là việc tính toán và kiểm tra độ vuông góc của các cấu trúc lớn như nhà cao tầng hay cầu đường.

Mối liên hệ giữa định lý Pytago và các định lý khác trong hình học

Định lý Pytago có mối liên hệ chặt chẽ với nhiều định lý quan trọng khác trong hình học. Định lý này không chỉ là nền tảng để chứng minh các định lý phức tạp hơn mà còn được ứng dụng rộng rãi trong việc giải các bài toán hình học.

Sự kết hợp giữa định lý này với các định lý khác tạo nên những công cụ mạnh mẽ để giải quyết các bài toán phức tạp. Đặc biệt trong các bài toán về tam giác, đường tròn và hình học không gian.

Định lý Pytago và định lý Tales

Định lí pitago và định lý talet có mối quan hệ bổ trợ cho nhau trong nhiều bài toán hình học. Khi áp dụng định lý Tales để chia tỷ số các đoạn thẳng, định lý Pytago giúp tính được độ dài chính xác của các cạnh.

Trong các bài toán về tam giác đồng dạng, việc kết hợp hai định lý này giúp giải quyết nhiều tình huống phức tạp. Ví dụ khi cần tìm tỷ số đồng dạng của hai tam giác vuông, ta có thể dùng định lý Tales để thiết lập tỷ số, sau đó áp dụng định lý Pytago để kiểm chứng.

Định lý Pytago và các bài toán về đường tròn

Định lí pi ta go đóng vai trò then chốt trong việc giải các bài toán liên quan đến đường tròn. Định lý này giúp tính được độ dài dây cung, khoảng cách từ tâm đến dây, bán kính đường tròn nội tiếp và ngoại tiếp tam giác.

Trong trường hợp đường tròn nội tiếp tam giác vuông, định lý Pytago kết hợp với các công thức diện tích giúp tìm được bán kính đường tròn một cách dễ dàng. Tương tự, với đường tròn ngoại tiếp, định lý này giúp thiết lập mối quan hệ giữa các cạnh và bán kính.

Định lý Pytago trong không gian ba chiều

Trong không gian ba chiều, định lý Pytago được mở rộng để tính khoảng cách giữa hai điểm bất kỳ. Công thức này trở thành công cụ cơ bản trong hình học không gian và được ứng dụng rộng rãi trong thực tế.

Khi xét các khối đa diện, định lý này giúp tính được độ dài đường chéo, khoảng cách từ đỉnh đến mặt phẳng, góc giữa đường thẳng và mặt phẳng. Đây là cơ sở để giải quyết nhiều bài toán phức tạp trong hình học không gian.

Việc áp dụng định lý trong không gian ba chiều đòi hỏi sự hiểu biết sâu sắc về phép chiếu vuông góc và các quan hệ hình học cơ bản. Điều này mở rộng khả năng ứng dụng của định lý trong các lĩnh vực như kiến trúc, xây dựng và thiết kế 3D.

Khi tìm hiểu về định lý Pytago, chúng ta không chỉ nắm vững công thức mà còn nhận ra tầm quan trọng của nó trong hình học và giải bài tập. Các khái niệm như định lý Pytago đảo cũng mở rộng ứng dụng thực tiễn, nhất là trong việc kiểm tra tính vuông góc của tam giác. Kiến thức vững chắc về định lý này sẽ giúp học sinh phát triển tư duy logic và giải quyết bài toán hiệu quả.