Tính chất và ứng dụng của sinx + cosx trong toán học và lượng giác

Sinx + cosx bằng gì? Đây là câu hỏi thú vị trong lượng giác, mở đầu cho những khám phá về tính chất và ứng dụng của hàm số này. Biểu thức này không chỉ đơn thuần là tổng của hai hàm số, mà còn liên quan đến những công thức và hình học sâu sắc. Khám phá ngay những thông tin quan trọng để hiểu rõ hơn về sinx + cosx trong toán học!

sinx + cosx bằng gì?

Biểu thức sinx + cosx bằng gì có thể được biểu diễn dưới dạng √2sin(x + π/4). Đây là một trong những công thức lượng giác quan trọng được sử dụng phổ biến trong toán học và các ứng dụng thực tế.

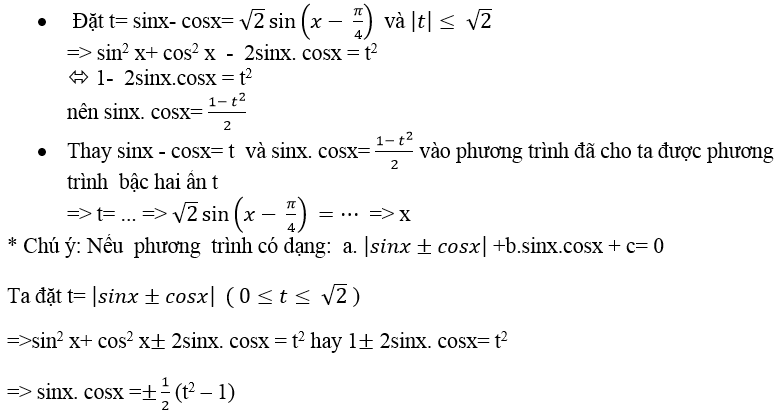
Để hiểu rõ hơn về biểu thức sinx+cosx bằng gì, ta có thể áp dụng phương pháp biến đổi lượng giác. Khi đó, sinx + cosx = √2[sin(x)cos(π/4) + cos(x)sin(π/4)] do sin(π/4) = cos(π/4) = 1/√2. Sau khi rút gọn, ta được kết quả cuối cùng là √2sin(x + π/4).

Trong nhiều bài toán phức tạp, việc biến đổi âm cộng dương bằng gì thường được áp dụng song song với công thức này. Điều này giúp đơn giản hóa các phép tính và tìm ra lời giải nhanh chóng hơn. Ví dụ như khi giải các phương trình lượng giác có dạng sinx + cosx = k, ta có thể đưa về dạng √2sin(x + π/4) = k để giải quyết dễ dàng hơn.

Các tính chất cơ bản của biểu thức sinx + cosx trong lượng giác

Biểu thức sinx + cosx là một trong những biểu thức lượng giác cơ bản và thường xuyên xuất hiện trong các bài toán. Biểu thức này có mối liên hệ chặt chẽ với định lý hàm cos và các công thức lượng giác khác.

Để hiểu rõ hơn về tính chất của biểu thức này, ta cần phân tích các đặc điểm quan trọng như giá trị cực trị, chu kỳ và đồ thị của nó. Mỗi tính chất sẽ giúp ta có cái nhìn toàn diện về cách biểu thức này hoạt động trong không gian lượng giác.

Giá trị lớn nhất và nhỏ nhất của sinx + cosx

Để tìm giá trị lớn nhất và nhỏ nhất, ta có thể biến đổi biểu thức thành dạng √2.sin(x + π/4) thông qua công thức biến đổi tổng thành tích. Từ đó ta thấy giá trị lớn nhất của biểu thức là √2 (khi x = π/4 + 2kπ) và giá trị nhỏ nhất là -√2 (khi x = 5π/4 + 2kπ).

Điều này có ý nghĩa quan trọng trong việc giải các bất phương trình và tìm miền giá trị của các biểu thức chứa sinx + cosx. Giá trị này cũng thường được sử dụng trong các ứng dụng thực tế như phân tích dao động điều hòa.

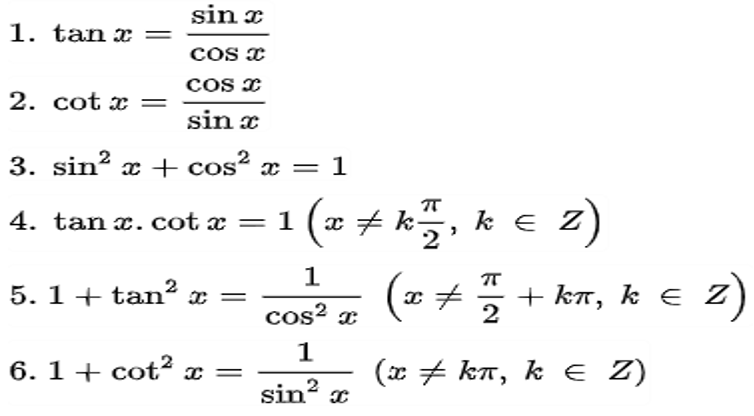
Chu kỳ của biểu thức sinx + cosx

Chu kỳ của biểu thức sinx + cosx là 2π, giống như chu kỳ của hàm sin và cos riêng lẻ. Điều này được chứng minh thông qua việc xét tính chất tuần hoàn của các hàm lượng giác cơ bản.

Khi x tăng thêm 2π, cả sin(x+2π) và cos(x+2π) đều trở về giá trị sin(x) và cos(x) ban đầu. Do đó tổng của chúng cũng có cùng tính chất tuần hoàn với chu kỳ 2π.

Đồ thị của hàm số y = sinx + cosx

Đồ thị của hàm số y = sinx + cosx là một đường cong hình sin dịch chuyển, có biên độ √2 và được dịch pha so với hàm sin thuần túy một góc π/4. Đường cong này cắt trục hoành tại các điểm x = 3π/4 + kπ, với k là số nguyên.

Đồ thị thể hiện tính tuần hoàn của hàm với chu kỳ 2π và dao động đều đặn giữa giá trị cực đại √2 và cực tiểu -√2. Hình dạng của đồ thị giúp ta hình dung rõ ràng về sự biến thiên của hàm số và các điểm đặc biệt của nó.

Phương pháp biến đổi và đơn giản hóa biểu thức sinx + cosx

Biểu thức simplify sinx + cosx là một trong những biểu thức lượng giác cơ bản thường gặp trong toán học. Việc biến đổi và đơn giản hóa biểu thức này giúp ta dễ dàng tính toán và giải quyết các bài toán phức tạp hơn.

Có nhiều phương pháp khác nhau để biến đổi biểu thức này thành dạng đơn giản hơn. Hai cách phổ biến nhất là chuyển về dạng √2.sin(x + π/4) hoặc sử dụng các công thức biến đổi tương đương khác. sin sang cos

Chuyển đổi sinx + cosx về dạng √2.sin(x + π/4)

Để chuyển đổi biểu thức sinx + cosx về dạng √2.sin(x + π/4), ta cần áp dụng công thức cộng của hàm sin. Đầu tiên, nhân cả tử và mẫu cho √2, ta được:
(sinx + cosx) = √2/√2(sinx + cosx) = √2(sinx/√2 + cosx/√2)

Tiếp theo, áp dụng công thức sin(A + B) = sinA.cosB + cosA.sinB với A = x và B = π/4, ta thu được kết quả cuối cùng là √2.sin(x + π/4).

Các dạng biến đổi tương đương khác

Ngoài cách biến đổi về dạng √2.sin(x + π/4), biểu thức sinx + cosx identity còn có thể được biến đổi theo nhiều cách khác. Một trong những cách phổ biến là sử dụng công thức lượng giác kép.

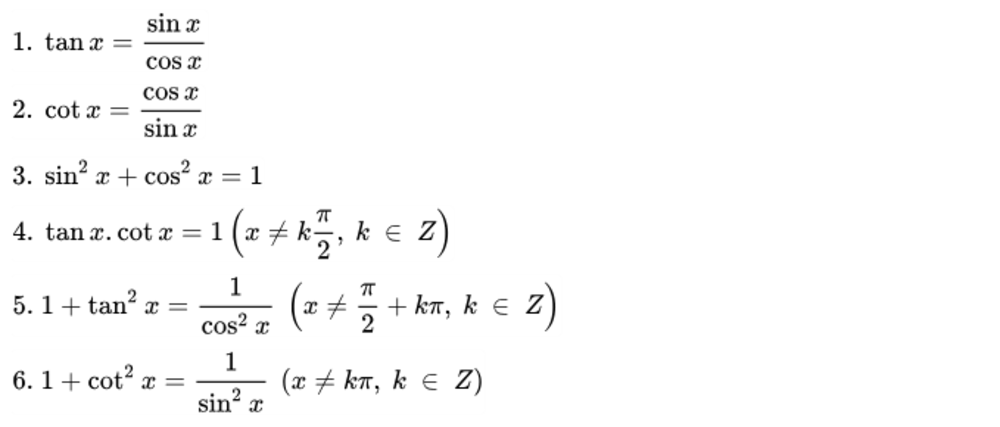
Ta có thể viết lại biểu thức dưới dạng 2sin(x/2)cos(x/2) + 2cos²(x/2) – 1. Cách này đặc biệt hữu ích khi giải các phương trình lượng giác phức tạp.

Một phương pháp khác là sử dụng các hằng đẳng thức lượng giác để chuyển đổi về dạng R.sin(x + α), trong đó R và α là các hằng số. Phương pháp này thường được áp dụng trong các bài toán dao động điều hòa.

Các phép tính với biểu thức sinx + cosx trong giải tích

Biểu thức sinx + cosx là một trong những biểu thức lượng giác cơ bản và thường xuyên xuất hiện trong các bài toán giải tích. Biểu thức này có nhiều tính chất đặc biệt và ứng dụng quan trọng trong việc tính toán đạo hàm, tích phân cũng như giải các phương trình lượng giác.

Khi làm việc với biểu thức này, ta cần lưu ý rằng nó có thể được biến đổi thành dạng √2.sin(x + π/4) thông qua công thức lượng giác. Điều này giúp đơn giản hóa nhiều phép tính phức tạp và tạo điều kiện thuận lợi cho việc giải quyết các bài toán liên quan.

Đạo hàm của sinx + cosx

Đạo hàm của biểu thức lượng giác này tuân theo quy tắc đạo hàm tổng và các công thức đạo hàm cơ bản của hàm sin và cos. Khi tính đạo hàm của sinx, ta được cosx. Ngược lại, đạo hàm của cosx cho kết quả là -sinx.

Khi kết hợp hai kết quả này, đạo hàm của formula for sinx + cosx sẽ là cosx – sinx. Đây là một kết quả quan trọng thường được sử dụng trong việc tìm cực trị của hàm số hoặc khảo sát sự biến thiên.

Tích phân của sinx + cosx

Tích phân của biểu thức này được thực hiện bằng cách tích phân từng thành phần riêng biệt. Khi tích phân sinx, ta được -cosx + C, và khi tích phân cosx, kết quả là sinx + C.

Vậy tích phân của sinx + cosx derivative sẽ cho kết quả là sinx – cosx + C. Công thức này có ý nghĩa quan trọng trong việc tính diện tích các hình phẳng giới hạn bởi đường cong y = sinx + cosx và trục hoành, cũng như trong nhiều ứng dụng thực tế khác của giải tích.

Ứng dụng của biểu thức sinx + cosx trong bài toán thực tế

Biểu thức sinx + cosx có nhiều ứng dụng quan trọng trong việc giải quyết các bài toán thực tiễn, đặc biệt trong lĩnh vực vật lý và kỹ thuật. Theo Hocthenao.vn, biểu thức này thường xuất hiện trong các phương trình dao động và các bài toán hình học lượng giác.

Việc áp dụng biểu thức này giúp đơn giản hóa nhiều tính toán phức tạp và mô tả chính xác các hiện tượng trong thực tế. Các ứng dụng chính bao gồm hai nhóm bài toán cơ bản là dao động điều hòa và các bài toán về góc trong tam giác lượng giác.

Bài toán dao động điều hòa

Trong vật lý, dao động điều hòa là một dạng chuyển động tuần hoàn quan trọng. Phương trình dao động điều hòa thường chứa tổng của hàm sin và cos để mô tả chính xác vị trí của vật theo thời gian.

Khi một vật dao động, vị trí của nó có thể được biểu diễn dưới dạng x = Asin(ωt) + Bcos(ωt), trong đó A và B là các hằng số phụ thuộc vào điều kiện ban đầu. Việc hiểu và vận dụng tốt biểu thức này giúp các kỹ sư thiết kế chính xác các hệ thống giảm xóc, máy móc công nghiệp.

Bài toán về góc và tam giác lượng giác

Trong hình học, biểu thức sin và cos kết hợp thường xuất hiện khi giải các bài toán liên quan đến tam giác và góc. Các công thức này đặc biệt hữu ích trong việc tính toán khoảng cách, độ cao và góc trong các ứng dụng thực tế như xây dựng, đo đạc địa hình.

Ví dụ trong ngành xây dựng, khi cần xác định độ nghiêng của một mái nhà, kỹ sư thường sử dụng tỷ số giữa chiều cao và chiều dài cơ sở, điều này liên quan trực tiếp đến biểu thức sin và cos của góc nghiêng. Việc tính toán chính xác các góc này đảm bảo độ an toàn và tính thẩm mỹ của công trình.

Trong lĩnh vực hàng hải, các thuyền trưởng sử dụng các công thức lượng giác để xác định hướng đi và vị trí của tàu dựa trên các góc đo được từ các điểm mốc trên bờ hoặc các thiên thể.

Các biểu thức liên quan đến sinx và cosx thường gặp

Trong lượng giác, các biểu thức chứa sinx và cosx xuất hiện rất phổ biến và có nhiều ứng dụng quan trọng. Hai biểu thức cơ bản nhất là tích và hiệu của chúng, mỗi biểu thức đều mang những đặc điểm và ý nghĩa riêng trong việc giải các bài toán lượng giác.

Việc nắm vững các công thức liên quan đến sinx và cosx giúp đơn giản hóa nhiều phép tính phức tạp, đặc biệt trong các bài toán về dao động điều hòa và phân tích Fourier. Các biểu thức này thường xuất hiện dưới dạng tích hoặc hiệu và có thể biến đổi qua lại giữa các dạng khác nhau.

Tích sinx.cosx và ý nghĩa

sinx.cosx bằng gì là câu hỏi thường gặp trong học tập. Tích này bằng 1/2.sin(2x), đây là một trong những công thức lượng giác cơ bản nhất. cosx.sinx bằng gì cũng cho kết quả tương tự do tính chất giao hoán của phép nhân.

Ý nghĩa hình học của tích này thể hiện rõ trong việc tính diện tích các hình có liên quan đến đường tròn lượng giác. Trong vật lý, công thức này đóng vai trò quan trọng khi nghiên cứu về sóng và dao động, đặc biệt trong hiện tượng giao thoa sóng.

Các nhà khoa học tại MIT đã ứng dụng công thức này trong việc phát triển các thuật toán xử lý tín hiệu số, giúp tối ưu hóa việc truyền tải dữ liệu trong các hệ thống viễn thông hiện đại.

Hiệu sinx – cosx và đặc điểm

sinx-cosx bằng gì là một biểu thức không thể đơn giản hóa thành một hàm lượng giác đơn lẻ như tích của chúng. sinx – cosx bằng gì thường được biến đổi thành dạng √2.sin(x – π/4) để thuận tiện trong tính toán.

Đặc điểm quan trọng của hiệu này là chu kỳ 2π và tính đối xứng qua điểm gốc. Biểu thức này có giá trị cực trị là ±√2, xuất hiện tại các điểm x = π/4 + πn, với n là số nguyên.

Trong thực tế, hiệu sinx – cosx thường được ứng dụng trong các bài toán về dao động điều hòa tổng hợp, nơi cần phân tích sự chênh lệch giữa hai thành phần dao động vuông góc với nhau. Các kỹ sư âm thanh sử dụng biểu thức này trong việc thiết kế bộ lọc tín hiệu và xử lý âm thanh kỹ thuật số.

Khi nghiên cứu về sinx + cosx bằng gì, bạn sẽ khám phá được nhiều tính chất thú vị của biểu thức này trong lượng giác. Biểu thức không chỉ có giá trị lớn nhất và nhỏ nhất rõ ràng mà còn có đồ thị mô tả các đặc điểm của hàm số. Hơn nữa, những biến đổi khi đơn giản hóa biểu thức cũng giúp bạn dễ dàng áp dụng vào thực tiễn trong các bài toán liên quan đến dao động hay tam giác lượng giác.