Công thức Logarit là một nội dung toán học thường xuyên được sử dụng trong suốt quá trình học trung học phổ thông và đại học. Logarit luôn được đánh giá là mảng kiến thức khó học vì có nhiều công thức dễ nhầm lẫn với nhau. Bài viết dưới đây, chúng tôi sẽ cung cấp cho bạn toàn bộ các công thức Logarit theo chương trình mới nhất năm 2024.
Giới thiệu chung về Logarit
Logarit là một phép toán nghịch đảo của lũy thừa, cho phép “giải” phương trình mũ.
Logarit cơ số a của một số dương x, ký hiệu là log_a(x), là số mũ y mà cơ số a phải lũy thừa để cho ra kết quả x. Nói cách khác, nếu a^y = x, thì y = log_a(x). Trong định nghĩa này, a được gọi là cơ số của logarit và phải là một số dương khác 1. Số x, được gọi là đối số của logarit, phải là một số dương.
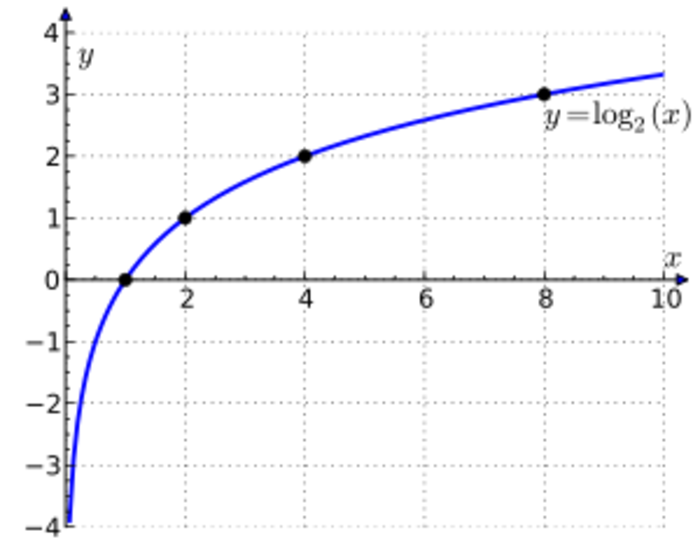
Logarit có ứng dụng rộng rãi trong nhiều lĩnh vực, từ việc đơn giản hóa các phép tính phức tạp đến việc mô tả các hiện tượng trong tự nhiên như cường độ động đất, âm thanh, hay độ pH. Các công thức Logarit cũng là công cụ quan trọng trong việc chuyển đổi các mối quan hệ phi tuyến thành các mối quan hệ tuyến tính, giúp đơn giản hóa nhiều bài toán trong khoa học và kỹ thuật.
Các công thức cơ bản của Logarit
Dưới đây là tổng hợp công thức Logarit chi tiết và đầy đủ nhất.
Logarit của tích và thương
Đối với tích, chúng ta có công thức:
$$\log_{a\;}(x\times y)=\log_{a\;}(y)$$
Còn đối với thương, công thức là:
$$\log_{a\;}(\frac xy)=\log_{a\;}(x)-\log_{a\;}(y)$$
Công thức Logarit của tích và thương là hai công thức quan trọng giúp đơn giản hóa các phép tính phức tạp. Hai ct logarit này cho phép chuyển đổi phép nhân và chia thành phép cộng và trừ tương ứng, làm cho các phép tính trở nên dễ dàng hơn.
Logarit của lũy thừa
Logarit của lũy thừa được biểu diễn bằng công thức:
$$\log_{a\;}(x^n)=n\times\log_{a\;}(x)$$
Công thức Log này rất hữu ích khi làm việc với các số mũ lớn hoặc phức tạp, cho phép chúng ta đơn giản hóa các biểu thức mũ thành các phép nhân đơn giản hơn.
Đổi cơ số Logarit
Với a và b là các cơ số logarit bất kỳ (thỏa mãn 0 < a ≠ 1 và 0 < b ≠ 1) và x là một số thực dương, ta có:
- $$\log_{a\;}(x)=\;\frac{\log_{b\;}(x)}{\log_{b\;}(a)}\;hay\;\log_{b\;}(a)\times\;\log_{a\;}(x)=\log_{b\;}(x)$$
- $$\log_{a\;}(x)=\;\frac1{\log_{X^a}}\;hay\;\log_{a\;}(x)\;\times\;\log_{x\;}(a)=1$$
- $$\log_{a^\alpha\;}(x)=\;\frac1\alpha\;\log_{a\;}(x)$$
- $$a^{\log_bc}=c^{\log_ba}$$
Công thức đổi cơ số logarit là một công cụ quan trọng cho phép chuyển đổi giữa các hệ logarit khác nhau. Điều này đặc biệt hữu ích khi cần làm việc với nhiều loại logarit khác nhau trong cùng một bài toán.
Các công thức Logarit đặc biệt
Các công thức đặc biệt như logarit của 1 (log_a(1) = 0) và logarit của cơ số (log_a(a) = 1) là những trường hợp cơ bản nhưng quan trọng. Chúng thường được sử dụng trong việc đơn giản hóa các biểu thức logarit phức tạp.
Logarit của căn thức, được biểu diễn bằng công thức:
$$\log_a\sqrt x=\frac12\times\log_a(x)$$
Đây là một ứng dụng đặc biệt của logarit của lũy thừa. Các công thức Loga này rất hữu ích khi làm việc với các biểu thức chứa căn bậc hai.
Cuối cùng, điều quan trọng cần lưu ý là logarit của số âm không xác định trong tập số thực. Đây là một hạn chế cơ bản của logarit khi làm việc trong hệ số thực, và cần được xem xét cẩn thận khi giải quyết các bài toán liên quan đến logarit. Dưới đây là bảng công thức Logarit đầy đủ nhất.
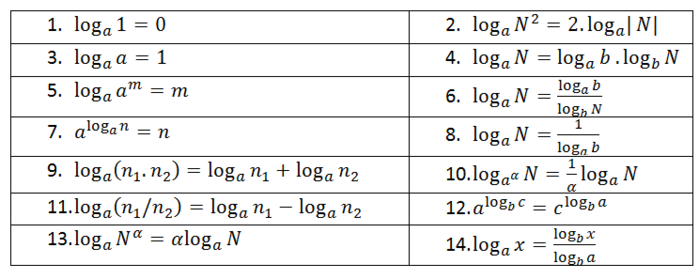
Các công thức mũ logarit cơ bản
Các công thức hàm số mũ cơ bản là nền tảng quan trọng trong toán học, đặc biệt khi làm việc với các biểu thức lũy thừa. Dưới đây là những công thức chính:
Tích, thương của các lũy thừa
Tích của các lũy thừa cùng cơ số được tính bằng cách giữ nguyên cơ số và cộng các số mũ:
$$a^m\times\;{a^n=a^{\left(m+n\right)}}$$
Công thức mũ này cho phép đơn giản hóa các biểu thức chứa nhiều lũy thừa của cùng một cơ số.
Thương của các lũy thừa cùng cơ số được tính bằng cách giữ nguyên cơ số và trừ các số mũ:
$$\frac{a^m}{a^n}\;{=a^{\left(m-n\right)}}$$
Đây là công thức đối ngẫu của tích lũy thừa, giúp xử lý các phép chia giữa các lũy thừa.
Lũy thừa của các lũy thừa
Lũy thừa của lũy thừa được tính bằng cách giữ nguyên cơ số và nhân các số mũ:
$$\left(a^m\right)^n=a^{m\times n}$$
Công thức này đặc biệt hữu ích khi cần tính toán với các lũy thừa lồng nhau.
Lũy thừa của tích được tính bằng cách lũy thừa từng thừa số:
$$\left(a\times b\right)^n=a^n\times b^n$$
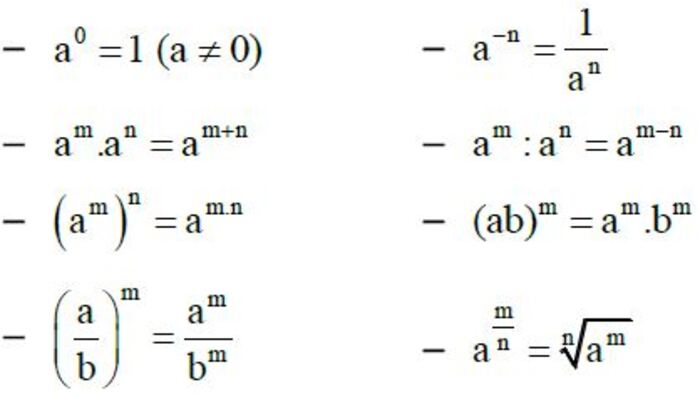
Tương tự, lũy thừa của thương được tính là:
$$\left(\frac ab\right)^n\;{=\frac{a^n}{b^n}}$$
Hai công thức này cho phép phân tách các lũy thừa phức tạp thành các thành phần đơn giản hơn.
Các trường hợp đặc biệt
Đối với số mũ âm, ta có công thức:
$$a^{\left(-n\right)}{=\frac1{a^n}}$$
Công thức số mũ này giúp chuyển đổi giữa lũy thừa dương và âm, đồng thời liên kết chặt chẽ với khái niệm về phân số.
Lũy thừa với số mũ 0 của bất kỳ số nào (trừ 0) đều bằng 1: a^0 = 1 (a ≠ 0). Đây là một trường hợp đặc biệt quan trọng trong nhiều tính toán.
Cuối cùng, đối với số mũ phân số, ta có công thức:
$$a^\frac mn=\sqrt[n]{a^m}$$
Công thức hàm số mũ Logarit này mở rộng khái niệm lũy thừa sang các số mũ không phải số nguyên, liên kết chặt chẽ với khái niệm về căn thức.
Ứng dụng thực tiễn của mũ và Logarit trong thực tế
Các công thức mũ và Logarit có nhiều ứng dụng trong thực tế, đóng vai trò thiết yếu trong nhiều lĩnh vực khoa học và đời sống hàng ngày:
- Tài chính: Lãi kép, tăng trưởng kinh tế, tỷ lệ lợi nhuận
- Vật lý: Phân rã phóng xạ, thang đo Richter (động đất)
- Sinh học: Tăng trưởng quần thể vi khuẩn, thang đo pH
- Âm học và điện tử: Thang đo decibel
- Khoa học máy tính: Thuật toán tìm kiếm và sắp xếp, mã hóa
- Y học: Dược động học, mô hình dịch tễ học
- Tâm lý học: Định luật Weber-Fechner (cảm nhận kích thích)
- Địa chất học: Đo độ axit của đất và nước
- Thiên văn học: Thang đo độ sáng sao
- Kỹ thuật: Tính toán độ bền vật liệu
Có thể thấy các công thức Logarit đầy đủ là những công cụ toán học mạnh mẽ với ứng dụng rộng rãi trong nhiều lĩnh vực của khoa học, kỹ thuật và đời sống hàng ngày
Lời kết
Công thức Logarit là một nội dung khá khó tiếp cận. Nó sở hữu khối lượng kiến thức đồ sộ, dễ nhầm lẫn với nhau. Tuy nhiên các công thức này lại có những ứng dụng quan trọng trong hầu hết các lĩnh vực hiện nay.