Công thức nguyên hàm cơ bản và phương pháp tính toán hiệu quả cho học sinh lớp 12

Công thức nguyên hàm là một phần quan trọng trong giải tích, cung cấp kiến thức cần thiết cho việc tính toán hàm số. Bài viết sẽ hướng dẫn chi tiết về bảng công thức nguyên hàm, phương pháp tính và ứng dụng trong các bài toán phổ biến, giúp bạn củng cố kỹ năng toán học hiệu quả.

Công thức nguyên hàm và các khái niệm cơ bản trong tính toán nguyên hàm

Nguyên hàm là một khái niệm quan trọng trong giải tích số, được định nghĩa là một hàm số mà đạo hàm của nó bằng hàm số ban đầu. Nói cách khác, nếu F(x) là nguyên hàm của f(x) thì F'(x) = f(x). Nguyên hàm của một hàm số không phải là duy nhất mà luôn tồn tại vô số nguyên hàm, chỉ khác nhau một hằng số.

Các công thức nguyên hàm cơ bản được xây dựng dựa trên quy tắc đạo hàm ngược. Ví dụ, nguyên hàm của hàm số xn là (xn+1)/(n+1) + C, với n ≠ -1 và C là hằng số tùy ý. Đối với hàm lượng giác, nguyên hàm của sin(x) là -cos(x) + C, và nguyên hàm của cos(x) là sin(x) + C.

Việc tính nguyên hàm đóng vai trò then chốt trong nhiều ứng dụng thực tế, từ tính diện tích dưới đường cong đến tính thể tích vật thể quay. Trong vật lý, nguyên hàm giúp tính công của lực, động năng của vật chuyển động. Trong kinh tế, nguyên hàm được sử dụng để tính tổng lợi nhuận hay chi phí tích lũy theo thời gian.

Bảng công thức nguyên hàm cơ bản và cách áp dụng trong giải toán

Việc nắm vững bảng công thức nguyên hàm cơ bản là nền tảng quan trọng để giải các bài toán tích phân. Tương tự như bảng đạo hàm, bảng nguyên hàm cung cấp các công thức tính sẵn giúp rút ngắn thời gian giải toán và tránh sai sót trong quá trình tính toán.

Bảng nguyên hàm cơ bản bao gồm các công thức tính nguyên hàm của các hàm số cơ bản như hàm lũy thừa, hàm mũ, hàm logarit và các hàm lượng giác. Mỗi công thức đều có điều kiện áp dụng riêng và cần được ghi nhớ chính xác để sử dụng hiệu quả.

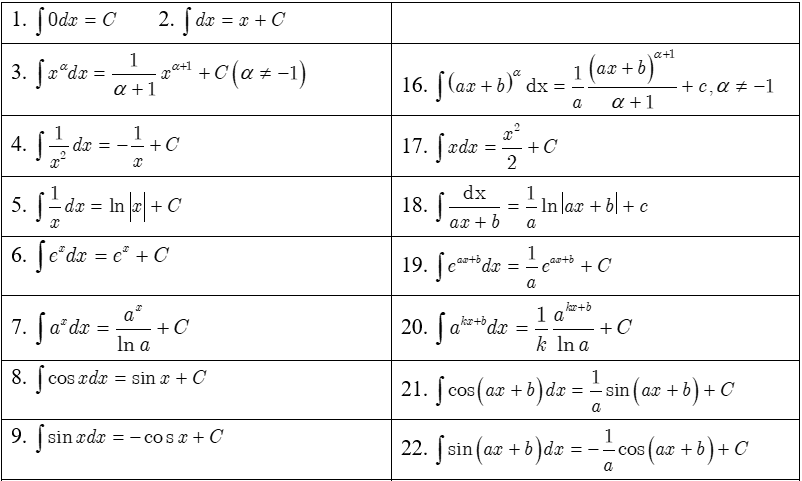
Khi áp dụng công thức nguyên hàm cơ bản, cần chú ý thêm hằng số tích phân C vào kết quả cuối cùng. Đây là điểm khác biệt quan trọng so với đạo hàm, vì một hàm số có thể có vô số nguyên hàm khác nhau, chỉ khác nhau một hằng số. Việc xác định giá trị của C phụ thuộc vào điều kiện cụ thể của từng bài toán.

Để sử dụng hiệu quả các công thức này, cần thực hành giải nhiều dạng bài tập khác nhau, từ cơ bản đến nâng cao. Việc thành thạo các kỹ thuật biến đổi và nhận dạng dạng toán sẽ giúp việc áp dụng công thức trở nên linh hoạt và chính xác hơn.

Phương pháp tính nguyên hàm của các dạng hàm số phổ biến

Tính nguyên hàm là một kỹ năng quan trọng trong giải tích, giúp ta tìm được hàm gốc từ một hàm đã cho. Việc nắm vững các phương pháp tính nguyên hàm của hàm số sẽ giúp giải quyết nhiều bài toán phức tạp trong thực tế. Dưới đây là các phương pháp tính nguyên hàm cho từng dạng hàm cụ thể.

Nguyên hàm của hàm mũ và logarit

Đối với hàm mũ, nguyên hàm a^x có dạng tổng quát là (a^x)/ln(a) + C, trong đó C là hằng số tích phân. Trường hợp đặc biệt với cơ số e, nguyên hàm e sẽ là chính nó cộng với hằng số C. Điều này làm cho việc tính toán trở nên đơn giản hơn nhiều.

Với hàm logarit, ta cần lưu ý mối quan hệ giữa đạo hàm của log và nguyên hàm lnx. Việc hiểu rõ mối liên hệ này sẽ giúp việc tính toán trở nên chính xác và nhanh chóng hơn.

Nguyên hàm của hàm lượng giác

Nguyên hàm của các hàm lượng giác tuân theo quy tắc đối ngẫu. Khi tính nguyên hàm của sin(x), kết quả sẽ là -cos(x) + C. Ngược lại, nguyên hàm của cos(x) là sin(x) + C.

Với các hàm lượng giác phức tạp hơn như tan(x), cot(x), sec(x) và cosec(x), ta cần áp dụng các công thức biến đổi đặc biệt để đưa về dạng cơ bản trước khi tính nguyên hàm.

Nguyên hàm của các hàm đặc biệt

Các hàm đặc biệt như hàm hữu tỷ, hàm vô tỷ thường đòi hỏi phương pháp tính riêng. Với hàm hữu tỷ, ta thường sử dụng phương pháp phân tích thành phân số thành phần trước khi tính nguyên hàm.

Đối với hàm vô tỷ, việc đặt ẩn phụ và biến đổi về dạng tích phân của hàm hữu tỷ là phương pháp thường được áp dụng. Quá trình này đòi hỏi sự kiên nhẫn và kỹ năng biến đổi đại số tốt.

Các tính chất và quy tắc tính nguyên hàm mở rộng

Nguyên hàm mở rộng là phép tính toán quan trọng trong giải tích, giúp tìm ra hàm số gốc từ đạo hàm của nó. Tính chất nguyên hàm và các quy tắc tính toán cần được nắm vững để áp dụng hiệu quả trong giải các bài toán phức tạp.

Việc thành thạo các phương pháp tính nguyên hàm sẽ giúp giải quyết nhiều dạng toán từ cơ bản đến nâng cao. Để tính nguyên hàm chính xác, cần nắm rõ các tính chất cơ bản và phương pháp tính phù hợp với từng dạng hàm số.

Tính chất cơ bản của nguyên hàm

Nguyên hàm của một hàm số luôn tồn tại vô số nghiệm, khác nhau một hằng số. Điều này xuất phát từ việc đạo hàm của một hằng số luôn bằng 0.

Khi tính đạo hàm nhanh của nguyên hàm, kết quả sẽ cho ra hàm số ban đầu. Đây là tính chất quan trọng giúp kiểm tra lại kết quả tính toán.

Nguyên hàm của tổng các hàm số bằng tổng nguyên hàm của từng hàm. Tương tự, nguyên hàm của tích một hằng số với một hàm số bằng tích hằng số đó với nguyên hàm của hàm số.

Phương pháp đổi biến số trong tính nguyên hàm

Phương pháp đổi biến số giúp đơn giản hóa biểu thức cần tính nguyên hàm bằng cách thay thế biến số ban đầu bằng một biến mới phù hợp. Việc chọn biến mới cần dựa vào dạng của hàm số.

Sau khi đổi biến và tính được nguyên hàm theo biến mới, cần thay ngược lại biến ban đầu để có kết quả cuối cùng. Phương pháp này đặc biệt hiệu quả với các hàm số có dạng phức tạp.

Một số trường hợp điển hình áp dụng phương pháp đổi biến như: hàm số chứa căn thức, hàm số mũ, hàm lượng giác phức tạp. Công thức nguyên hàm 12 thường được áp dụng kết hợp với phương pháp này.

Phương pháp tích phân từng phần

Phương pháp tích phân từng phần thường được áp dụng khi tính nguyên hàm của tích hai hàm số. Phương pháp này dựa trên công thức đạo hàm của tích.

Việc chọn u và dv trong công thức tích phân từng phần cần dựa vào kinh nghiệm và một số quy tắc. Thông thường, chọn u là hàm đơn giản hơn khi lấy đạo hàm.

Phương pháp này đặc biệt hiệu quả với các dạng tích của hàm mũ với hàm lượng giác, tích của hàm đa thức với hàm mũ hoặc hàm lượng giác. Trong một số trường hợp, có thể cần áp dụng phương pháp này nhiều lần liên tiếp.

Ứng dụng của công thức nguyên hàm trong giải toán lớp 12

Công thức nguyên hàm lớp 12 được ứng dụng rộng rãi trong việc giải các bài toán tích phân, diện tích và thể tích. Việc nắm vững các công thức cơ bản sẽ giúp học sinh dễ dàng vận dụng vào các dạng toán phức tạp hơn. Như Học Thế Nào đã đề cập, việc hiểu rõ nguyên lý và thực hành nhiều sẽ giúp nâng cao kỹ năng giải toán.

Để áp dụng hiệu quả các công thức tính nguyên hàm, học sinh cần kết hợp kiến thức về đạo hàm cấp cao với các phương pháp tính nguyên hàm. Điều này tạo nền tảng vững chắc cho việc giải quyết các bài toán phức tạp.

Bài tập về tính nguyên hàm cơ bản

Các bài tập về nguyên hàm cơ bản thường yêu cầu học sinh áp dụng trực tiếp công thức để tìm nguyên hàm của một hàm số cho trước. Việc nắm vững các công thức cơ bản là chìa khóa để giải quyết thành công các bài toán này.

Khi giải các bài tập nguyên hàm, học sinh cần chú ý đến hằng số tích phân và các trường hợp đặc biệt. Việc kiểm tra kết quả bằng cách lấy đạo hàm của nguyên hàm tìm được là một bước quan trọng để đảm bảo tính chính xác.

Bài tập về tích phân

Bài tập về tích phân đòi hỏi sự kết hợp giữa kỹ năng tính nguyên hàm và khả năng xác định cận tích phân. Học sinh cần phân tích kỹ yêu cầu bài toán để chọn phương pháp giải phù hợp.

Một số bài tập tích phân phức tạp có thể yêu cầu sử dụng phương pháp đổi biến hoặc tích phân từng phần. Việc thực hành nhiều dạng bài tập khác nhau sẽ giúp học sinh phát triển khả năng tư duy và linh hoạt trong cách giải.

Bài tập về diện tích và thể tích

Ứng dụng quan trọng của tích phân trong việc tính diện tích và thể tích đòi hỏi học sinh phải có khả năng hình dung không gian tốt. Các bài toán này thường liên quan đến việc xác định miền tích phân và thiết lập công thức tính toán phù hợp.

Khi giải các bài toán về diện tích, việc vẽ hình và xác định chính xác đường biên là bước quan trọng. Đối với bài toán thể tích, học sinh cần hiểu rõ phương pháp tính thể tích khối tròn xoay và các trường hợp đặc biệt.

Việc kết hợp kiến thức hình học không gian với kỹ năng tính tích phân sẽ giúp học sinh giải quyết thành công các bài toán phức tạp về diện tích và thể tích.

Công thức nguyên hàm là một phần quan trọng trong toán học, đặc biệt trong việc giải quyết các bài toán tích phân. Bài viết đã cung cấp những kiến thức cơ bản về bảng nguyên hàm, phương pháp tính và ứng dụng trong các bài tập thực tế. Việc nắm vững công thức nguyên hàm sẽ giúp học sinh lớp 12 tự tin hơn trong kỳ thi và áp dụng hiệu quả vào học tập.