Nguyên hàm lnx và các công thức tính toán logarit tự nhiên dễ hiểu

Nguyên hàm lnx là một phần quan trọng trong giải tích, có vai trò trong việc tìm hiểu các tính chất của hàm logarit tự nhiên. Bài viết này sẽ cung cấp các phương pháp tính toán, công thức cơ bản và ứng dụng thực tế của nguyên hàm lnx. Hãy cùng khám phá cách áp dụng hiệu quả trong các bài toán liên quan.

Nguyên hàm lnx là phép tính tích phân của logarit tự nhiên

Nguyên hàm lnx là một phép tính quan trọng trong giải tích, được sử dụng để tìm hàm gốc của hàm logarit tự nhiên. Công thức tổng quát của nguyên hàm của ln là xlnx – x + C, trong đó C là hằng số tích phân.

Khi áp dụng công thức này, ta cần chú ý rằng miền xác định của hàm logarit tự nhiên là tập các số dương. Do đó, nguyên hàm ln cũng chỉ có nghĩa khi biến x dương. Điều này có ý nghĩa quan trọng khi giải các bài toán liên quan đến tích phân.

Việc tính nguyên hàm của logarit tự nhiên thường được thực hiện thông qua phương pháp tích phân từng phần. Phương pháp này giúp ta xử lý các biểu thức phức tạp hơn có chứa hàm logarit, như tích của logarit với các hàm đa thức hoặc lũy thừa.

Các công thức tính nguyên hàm lnx cơ bản và phương pháp áp dụng

Việc tính nguyên hàm ln x đòi hỏi nắm vững các công thức cơ bản và phương pháp áp dụng phù hợp. Theo Học Thế Nào VN, sinh viên cần hiểu rõ bản chất của logarit tự nhiên để có thể áp dụng hiệu quả vào bài toán cụ thể.

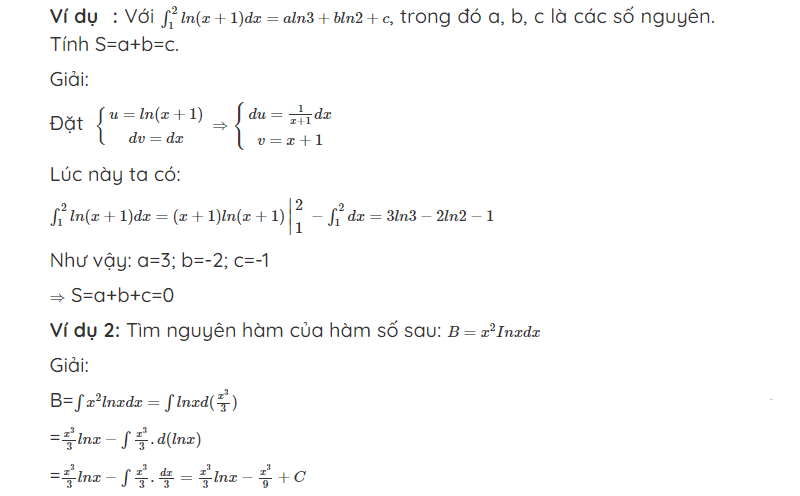
Khi giải các bài toán liên quan đến công thức ln(x), việc đầu tiên là xác định dạng của hàm số. Nếu là hàm đơn giản dạng ln(x), nguyên hàm sẽ là xlnx – x + C. Với các dạng phức tạp hơn, cần kết hợp các phương pháp tích phân như đổi biến số hoặc tích phân từng phần.

Để tính nguyên hàm lnx một cách chính xác, cần chú ý miền xác định của hàm số và điều kiện áp dụng công thức. Đối với các bài toán thực tế, việc kiểm tra kết quả bằng cách lấy đạo hàm của nguyên hàm thu được là bước quan trọng để đảm bảo tính chính xác của lời giải.

Phương pháp tính nguyên hàm của biểu thức chứa lnx

Việc tính nguyên hàm của ln x đòi hỏi sự linh hoạt trong việc áp dụng các phương pháp tích phân khác nhau. Tùy thuộc vào dạng biểu thức chứa lnx, ta có thể sử dụng phương pháp đổi biến số hoặc tích phân từng phần.

Khi gặp các biểu thức phức tạp chứa nguyên hàm của lnx, việc lựa chọn phương pháp phù hợp sẽ giúp đơn giản hóa quá trình tính toán. Mỗi phương pháp có những ưu điểm riêng và phù hợp với từng dạng biểu thức cụ thể.

Phương pháp đổi biến số với u = lnx

Khi biểu thức cần tích phân lnx có dạng phức tạp, việc đặt u = lnx thường mang lại hiệu quả cao. Phương pháp này giúp biến đổi biểu thức ban đầu thành dạng đơn giản hơn với biến u.

Sau khi đặt u = lnx, ta cần chú ý tới việc biến đổi dx thành du/x để đảm bảo tính chính xác của kết quả. Điều quan trọng là phải thực hiện đồng thời cả hai phép biến đổi này.

Phương pháp tích phân từng phần với lnx

Phương pháp tích phân từng phần thường được áp dụng khi lnx xuất hiện dưới dạng nhân với một hàm số khác. Công thức cơ bản là ∫udv = uv – ∫vdu, trong đó ta thường chọn u = lnx.

Việc lựa chọn đúng thành phần u và dv quyết định độ phức tạp của phép tính. Nếu chọn sai, ta có thể gặp phải các tích phân phức tạp hơn biểu thức ban đầu.

Khi áp dụng phương pháp này, cần kiểm tra kỹ lưỡng kết quả thu được để tránh sai sót trong quá trình tính toán.

Các trường hợp đặc biệt khi tính nguyên hàm lnx

Một số trường hợp đặc biệt như ∫lnx dx = xlnx – x + C hay ∫(lnx)² dx = x(lnx)² – 2xlnx + 2x + C cần được ghi nhớ để tiết kiệm thời gian tính toán.

Các công thức này thường xuất hiện trong nhiều bài toán và có thể được sử dụng làm cơ sở để giải quyết các bài toán phức tạp hơn. Việc nắm vững các trường hợp đặc biệt sẽ giúp quá trình tính toán trở nên nhanh chóng và chính xác hơn.

Ngoài ra, ta cũng cần lưu ý đến miền xác định của hàm số khi tính nguyên hàm có chứa lnx, vì lnx chỉ xác định khi x > 0.

Ứng dụng nguyên hàm lnx trong các bài toán thực tế

Nguyên hàm lnx có nhiều ứng dụng quan trọng trong việc giải quyết các bài toán thực tế, đặc biệt là tính toán diện tích và thể tích. Việc áp dụng công thức tích phân của hàm logarit tự nhiên giúp giải quyết nhiều bài toán phức tạp một cách hiệu quả.

Hai ứng dụng phổ biến nhất là tính diện tích giới hạn bởi đường cong logarit và tính thể tích vật thể xoay. Những bài toán này thường xuất hiện trong thiết kế kỹ thuật và nghiên cứu khoa học, đòi hỏi sự kết hợp giữa công thức nhị thức newton và tích phân logarit.

Bài toán tính diện tích giới hạn bởi đường cong y = lnx

Khi tính diện tích giới hạn bởi đường cong logarit, ta thường xét một vùng giới hạn bởi đường cong y = lnx, trục hoành và hai đường thẳng x = a và x = b. Diện tích này được tính bằng tích phân xác định của hàm logarit.

Trong thực tế, các kỹ sư xây dựng sử dụng phương pháp này để tính toán diện tích mặt cắt của các công trình có dạng logarit như mái vòm, cầu treo. Ví dụ, công ty thiết kế Bridge Engineering Ltd đã áp dụng phương pháp này để tính toán diện tích mặt cắt của cầu Golden Gate.

Việc áp dụng nguyen ham lnx trong tính toán diện tích đòi hỏi sự hiểu biết sâu sắc về tính chất của hàm logarit và kỹ năng tích phân. Kết quả thu được sẽ giúp tối ưu hóa thiết kế và tiết kiệm vật liệu xây dựng.

Bài toán tính thể tích vật thể xoay quanh trục Ox

Bài toán tính thể tích vật thể xoay được ứng dụng rộng rãi trong công nghiệp sản xuất, đặc biệt là thiết kế các sản phẩm có dạng hình trụ xoay. Lnx nguyên hàm đóng vai trò quan trọng trong việc tính toán thể tích này.

Phương pháp tính thể tích vật thể xoay được áp dụng trong nhiều ngành công nghiệp. Chẳng hạn như ngành sản xuất bình chứa, nơi các kỹ sư cần tính toán chính xác thể tích của các bình có dạng đặc biệt được tạo ra bởi đường cong logarit xoay quanh trục.

Trong ngành công nghiệp ô tô, các nhà thiết kế sử dụng phương pháp này để tối ưu hóa hình dạng của các bộ phận như ống xả, bình xăng. Toyota đã áp dụng thành công phương pháp này trong việc thiết kế hệ thống ống xả hiệu quả cho dòng xe Camry 2023.

Các dạng biến thể của nguyên hàm logarit tự nhiên

Nguyên hàm logarit tự nhiên có nhiều dạng biến thể khác nhau, mỗi dạng đều có những đặc điểm và cách giải riêng. Việc nắm vững các dạng này giúp giải quyết nhiều bài toán tích phân phức tạp.

Các biến thể thường gặp bao gồm nguyên hàm của hàm logarit đơn giản, nguyên hàm của tích hoặc thương giữa logarit với các hàm khác. Mỗi dạng đòi hỏi áp dụng các phương pháp tích phân khác nhau như đổi biến, tích phân từng phần.

Nguyên hàm của ln(u) với u là hàm số

Nguyên hàm của ln u là một trong những dạng cơ bản nhất. Khi u là một hàm số, ta thường áp dụng phương pháp đổi biến hoặc tích phân từng phần để tìm nguyên hàm.

Công thức tổng quát cho nguyên hàm ln(u) là: ∫ln(u)dx = uln(u) – u + C, trong đó u’ là đạo hàm của u theo x. Đây là công thức quan trọng cần ghi nhớ khi giải các bài toán liên quan.

Nguyên hàm của lnx/x và các biến thể

Nguyên hàm của lnx/x là một trường hợp đặc biệt thường xuất hiện trong các bài tập. Công thức tổng quát là: ∫(lnx/x)dx = (ln²x)/2 + C.

Khi gặp các biến thể phức tạp hơn như (lnx)²/x hay lnx/x², ta cần vận dụng linh hoạt các phương pháp tích phân cơ bản kết hợp với đổi biến để giải quyết. Nguyên hàm lnu trong những trường hợp này thường đòi hỏi kỹ năng phân tích và biến đổi phù hợp.

Bài tập mẫu và phương pháp giải

Xét bài toán: Tìm nguyen ham ln của biểu thức f(x) = ln(2x+1).
Bước 1: Đặt u = 2x+1

Bước 2: Áp dụng công thức ∫ln(u)dx = uln(u) – u + C
Bước 3: Kết quả: ∫ln(2x+1)dx = (2x+1)ln(2x+1) – (2x+1) + C

Một ví dụ khác với nguyen ham cua lnx: Tìm ∫(lnx)²dx
Phương pháp giải sử dụng tích phân từng phần hai lần:

• Lần 1: Đặt u = (lnx)², dv = dx
• Lần 2: Đặt u = lnx, dv = lnxdx

Kết quả: ∫(lnx)²dx = x(lnx)² – 2xlnx + 2x + C

Khi nghiên cứu về nguyên hàm lnx, bạn sẽ khám phá được nhiều phương pháp và ứng dụng thú vị trong toán học. Bài viết đã nêu rõ các công thức cơ bản, cách tính nguyên hàm của các biểu thức phức tạp và cách áp dụng vào thực tế. Việc nắm vững nguyên hàm không chỉ giúp bạn giải bài tập dễ dàng mà còn mở rộng hiểu biết về tích phân và ứng dụng của nó trong cuộc sống hàng ngày.