Công thức tính chu vi diện tích đường tròn và cách áp dụng trong toán học

Công thức tính chu vi diện tích đường tròn là kiến thức cơ bản trong hình học mà mọi học sinh cần nắm vững. Bằng cách hiểu và áp dụng công thức này, bạn có thể giải quyết nhiều bài toán toán học liên quan đến hình tròn một cách dễ dàng. Tìm hiểu các thành phần cơ bản, công thức, cách tính để nâng cao kỹ năng toán học của mình.

Công thức tính chu vi diện tích đường tròn và ý nghĩa trong toán học

Trong Hình học phẳng toán, công thức tính chu vi diện tích đường tròn là một trong những kiến thức nền tảng quan trọng. Với đường tròn có bán kính R, chu vi được tính bằng công thức C = 2πR, trong đó π ≈ 3,14. Còn diện tích đường tròn được tính theo công thức S = πR².

Ý nghĩa toán học của các công thức này thể hiện mối quan hệ chặt chẽ giữa các yếu tố của đường tròn. Chu vi đường tròn luôn gấp 2π lần bán kính, cho thấy tỷ lệ không đổi giữa chu vi và đường kính của mọi đường tròn. Điều này giúp ta dễ dàng tính toán kích thước của các vật thể hình tròn trong thực tế.

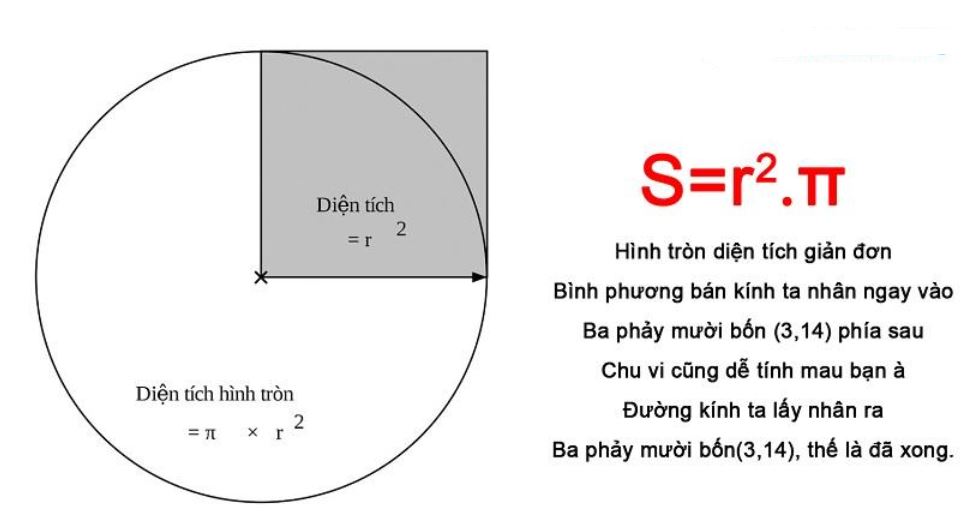
Về diện tích, công thức πR² phản ánh quy luật tăng trưởng theo bình phương của bán kính. Khi bán kính tăng gấp đôi, diện tích sẽ tăng gấp 4 lần. Đây là cơ sở quan trọng trong nhiều ứng dụng thực tiễn như thiết kế kiến trúc, quy hoạch đô thị hay tính toán trong kỹ thuật cơ khí.

Các thành phần cơ bản của hình tròn cần nắm vững để tính toán

Để tính toán chính xác công thức tính chu vi diện tích đường tròn, việc nắm vững các thành phần cơ bản của hình tròn là vô cùng quan trọng. Mỗi thành phần đều có vai trò riêng và mối liên hệ mật thiết với nhau trong các phép tính hình học.

Tâm và bán kính của đường tròn

Tâm là điểm nằm cách đều tất cả các điểm trên đường tròn. Đây là yếu tố quyết định vị trí của đường tròn trong mặt phẳng tọa độ. công thức tính tâm i và bán kính r giúp xác định chính xác các thông số này.

Bán kính là đoạn thẳng nối từ tâm đến một điểm bất kỳ trên đường tròn. Độ dài bán kính không đổi và là yếu tố quan trọng trong việc xác định kích thước của đường tròn.

Đường kính và mối quan hệ với bán kính

Đường kính là đoạn thẳng đi qua tâm và nối hai điểm đối diện trên đường tròn. Độ dài đường kính luôn bằng hai lần bán kính, tạo nên mối quan hệ cơ bản D = 2r.

Mối quan hệ này có ý nghĩa quan trọng trong nhiều bài toán thực tế. Ví dụ, khi thiết kế ống nước, kỹ sư thường sử dụng đường kính để mô tả kích thước, trong khi các tính toán lưu lượng lại dựa trên bán kính.

Số Pi (π) và vai trò trong tính toán

Số Pi là hằng số toán học đặc biệt, biểu thị tỷ số giữa chu vi và đường kính của mọi đường tròn. Giá trị gần đúng thường dùng là 3,14 hoặc 22/7.

Trong lịch sử toán học, các nhà khoa học đã tốn nhiều công sức nghiên cứu về số Pi. Archimedes (287-212 TCN) là người đầu tiên tính toán giá trị gần đúng của Pi bằng phương pháp đa giác nội tiếp và ngoại tiếp.

Số Pi đóng vai trò then chốt trong các công thức tính chu vi (C = 2πr) và diện tích (S = πr²) của hình tròn. Sự xuất hiện của Pi trong các công thức này phản ánh mối liên hệ tự nhiên và phổ quát giữa các yếu tố hình học của đường tròn.

Cách tính chu vi hình tròn chính xác và nhanh chóng

Để tính chu vi hình tròn bằng gì, cần nắm vững công thức cơ bản và các bước thực hiện. Việc tính toán chu vi hình tròn đóng vai trò quan trọng trong nhiều lĩnh vực từ toán học cơ bản đến ứng dụng thực tiễn như xây dựng, thiết kế.

Trước khi đi vào chi tiết cách tính, cần hiểu rõ mối quan hệ giữa chu vi và các yếu tố khác của hình tròn. Chu vi hình tròn luôn tỷ lệ thuận với bán kính và có mối liên hệ chặt chẽ với công thức phương trình đường tròn.

Công thức tính chu vi hình tròn cơ bản C = 2πR

Công thức C = 2πR là nền tảng để muốn tính chu vi hình tròn. Trong đó, C là chu vi hình tròn, π (pi) là hằng số có giá trị xấp xỉ 3,14 và R là bán kính hình tròn. Công thức này được phát hiện từ thời Hy Lạp cổ đại và vẫn được sử dụng phổ biến đến ngày nay.

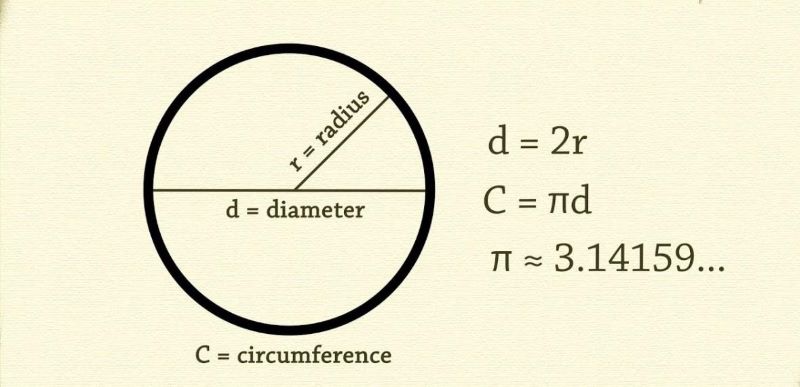
Giá trị của π có thể lấy chính xác đến nhiều chữ số thập phân tùy theo yêu cầu độ chính xác của bài toán. Trong tính toán thông thường, việc sử dụng π = 3,14 đã đủ độ chính xác cho hầu hết các ứng dụng thực tế.

Các bước tính chu vi hình tròn từ bán kính

Bước 1: Xác định chính xác bán kính R của hình tròn bằng cách đo từ tâm đến một điểm bất kỳ trên đường tròn.

Bước 2: Nhân bán kính với 2 để được 2R.

Bước 3: Nhân kết quả với π (3,14) để được chu vi hình tròn.

Việc thực hiện theo trình tự này giúp cách tính chu vi đường tròn trở nên đơn giản và tránh sai sót trong quá trình tính toán.

Ví dụ minh họa về tính chu vi hình tròn

Một ví dụ thực tế từ ngành xây dựng: Khi thiết kế bể chứa nước hình trụ, kiến trúc sư cần tính chu vi đáy để xác định lượng vật liệu cần thiết. Với bể có bán kính 2m, áp dụng công thức:

C = 2 × 3,14 × 2 = 12,56m

Một trường hợp khác trong thiết kế công nghiệp: Khi sản xuất ống thoát nước có bán kính 0,5m, chu vi ống được tính:

C = 2 × 3,14 × 0,5 = 3,14m

Những ví dụ này cho thấy việc tính chu vi hình tròn không chỉ là bài toán lý thuyết mà còn có nhiều ứng dụng thực tiễn quan trọng.

Phương pháp tính diện tích hình tròn hiệu quả

Việc tính diện tích hình tròn là một kỹ năng toán học cơ bản và thiết yếu. Phương pháp này giúp giải quyết nhiều bài toán thực tế như tính diện tích mặt bàn tròn, đáy bình chứa hay các công trình kiến trúc hình tròn.

Để tính chính xác diện tích, cần nắm vững công thức cơ bản và thực hành qua nhiều ví dụ. Việc áp dụng đúng phương pháp sẽ giúp kết quả tính toán chính xác và tiết kiệm thời gian.

Công thức tính diện tích hình tròn S = πR²

Công thức s hình tròn được xác định bằng tích của số π (pi ≈ 3,14) với bình phương bán kính. Đây là công thức phổ biến được áp dụng rộng rãi trong toán học và các ngành kỹ thuật.

Trong thực tế, giá trị π thường được làm tròn đến 2 chữ số thập phân là 3,14 để thuận tiện tính toán. Tuy nhiên với các bài toán yêu cầu độ chính xác cao, có thể sử dụng giá trị π = 3,14159.

Các bước tính diện tích hình tròn từ bán kính

Bước đầu tiên là xác định chính xác bán kính của hình tròn cần tính. Việc đo đạc cần thực hiện cẩn thận, sử dụng dụng cụ đo phù hợp như thước kẻ hay thước dây.

Tiếp theo, bình phương giá trị bán kính đã đo được. Đối với các số thập phân, cần chú ý giữ đúng số chữ số thập phân theo yêu cầu bài toán.

Cuối cùng, nhân kết quả với π để thu được diện tích đường tròn. Khi tính toán với công thức tính thể tích khối tròn xoay, ta có thể áp dụng kết quả này làm cơ sở.

Ví dụ thực hành tính diện tích hình tròn

Một ví dụ điển hình là tính diện tích mặt bàn tròn có bán kính 0,75m. Áp dụng công thức tính diện tích hình tròn, ta có:
S = π × 0,75² = 3,14 × 0,5625 = 1,77 m²

Trong công nghiệp, việc tính diện tích đáy bồn chứa hình tròn rất quan trọng. Với bồn chứa bán kính 2m, diện tích đáy sẽ là:
S = 3,14 × 2² = 12,56 m²

Kết quả tính toán giúp xác định chính xác lượng vật liệu cần thiết, từ đó tối ưu chi phí sản xuất và thi công.

Ứng dụng công thức tính chu vi diện tích đường tròn trong thực tế

Công thức tính chu vi diện tích đường tròn được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống. Từ thiết kế xây dựng, sản xuất công nghiệp đến các hoạt động thường ngày, công thức này giúp tính toán chính xác kích thước và diện tích các vật thể hình tròn.

Việc áp dụng công thức vào thực tế đòi hỏi sự linh hoạt và chính xác. Các kỹ sư, kiến trúc sư thường kết hợp công thức với các phần mềm thiết kế để tạo ra những công trình có độ chính xác cao.

Bài toán thực tế về chu vi hình tròn

Một công ty sản xuất đồng hồ cần tính lượng dây cao su để làm viền cho mặt đồng hồ có đường kính 4cm. Sử dụng công thức chu vi, họ tính được cần 12,56cm dây cao su cho mỗi sản phẩm. Điều này giúp tối ưu nguyên liệu và giảm chi phí sản xuất.

Trong thiết kế cảnh quan, các kiến trúc sư sử dụng công thức tính chu vi để xác định số lượng gạch lát cần thiết cho bồn hoa tròn hoặc đài phun nước. Việc tính toán chính xác giúp tiết kiệm vật liệu và tạo tính thẩm mỹ cao.

Bài toán thực tế về diện tích hình tròn

Theo nghiên cứu của Viện Kiến trúc Quốc gia, diện tích tròn được ứng dụng phổ biến trong thiết kế mái vòm. Ví dụ, một mái vòm có bán kính 5m sẽ cần 78,5m² vật liệu phủ. Việc tính toán chính xác giúp dự toán ngân sách và lên kế hoạch thi công hiệu quả.

Trong ngành công nghiệp thực phẩm, các nhà máy sản xuất bánh kẹo sử dụng công thức này để tính diện tích khuôn bánh, từ đó xác định lượng bột và nguyên liệu cần thiết. Điều này đảm bảo sản phẩm đồng đều và kiểm soát được chi phí.

Mối liên hệ với các hình học khác

Hình tròn có mối quan hệ mật thiết với nhiều hình học khác. Cách tính bán kính đường tròn ngoại tiếp tam giác là một ví dụ điển hình về sự kết hợp giữa hình tròn và tam giác trong toán học ứng dụng.

Trong không gian ba chiều, công thức tính bán kính mặt cầu được phát triển từ công thức của hình tròn. Mối liên hệ này thể hiện tính kế thừa và phát triển của toán học hình học.

Các công thức hình tròn còn được áp dụng trong tính toán diện tích hình trụ, hình nón và các hình học phức tạp khác. Sự kết hợp này tạo nên nền tảng cho nhiều ứng dụng trong kiến trúc và kỹ thuật hiện đại.

Các lỗi thường gặp khi tính chu vi và diện tích hình tròn

Khi áp dụng công thức tính chu vi diện tích đường tròn, nhiều người thường mắc phải một số sai lầm cơ bản. Việc hiểu rõ và tránh được những lỗi này sẽ giúp kết quả tính toán chính xác hơn. Dưới đây là phân tích chi tiết về các lỗi phổ biến và cách khắc phục.

Nhầm lẫn giữa bán kính và đường kính

Một trong những sai sót thường xuyên xảy ra là việc nhầm lẫn giữa bán kính và đường kính khi áp dụng công thức. Nhiều người sử dụng đường kính thay vì bán kính trong công thức diện tích S = πr², dẫn đến kết quả sai lệch gấp 4 lần.

Để tránh nhầm lẫn, cần xác định rõ đường kính bằng 2 lần bán kính. Trong một số trường hợp phức tạp như công thức định lý pytago đảo, việc phân biệt này càng trở nên quan trọng để tránh sai sót trong quá trình giải toán.

Sai sót khi sử dụng số Pi

Việc làm tròn số Pi không phù hợp có thể dẫn đến sai số đáng kể. Một số người chỉ sử dụng π = 3.14, trong khi các bài toán yêu cầu độ chính xác cao hơn cần dùng π = 3.14159.

Khi áp dụng công thức tính đường cao kết hợp với tính toán hình tròn, việc chọn giá trị Pi phù hợp càng quan trọng. Tùy theo yêu cầu độ chính xác của bài toán, ta có thể sử dụng các giá trị Pi khác nhau, nhưng cần đảm bảo tính nhất quán trong toàn bộ quá trình tính toán.

Cách kiểm tra kết quả tính toán

Để đảm bảo kết quả chính xác, cần thực hiện kiểm tra theo nhiều phương pháp khác nhau. Phương pháp đơn giản nhất là ước lượng kết quả trước khi tính chi tiết, giúp phát hiện những sai sót lớn.

Một cách kiểm tra khác là sử dụng mối quan hệ giữa chu vi và diện tích. Nếu chu vi tăng gấp đôi, diện tích sẽ tăng gấp 4 lần. Việc nắm vững các mối quan hệ này giúp phát hiện nhanh các kết quả bất thường trong quá trình tính toán.

Ngoài ra, việc sử dụng công cụ tính toán trực tuyến để đối chiếu kết quả cũng là một phương pháp hiệu quả. Tuy nhiên, không nên phụ thuộc hoàn toàn vào công cụ mà cần hiểu rõ nguyên lý tính toán cơ bản.

Cuối cùng, công thức tính chu vi diện tích đường tròn đóng vai trò quan trọng trong việc giải quyết nhiều bài toán hình học. Bằng cách hiểu rõ các thành phần như bán kính, đường kính và số Pi, bạn có thể dễ dàng tính toán chu vi và diện tích hình tròn. Những phương pháp này không chỉ đơn giản mà còn áp dụng rộng rãi trong thực tế, giúp nâng cao khả năng tư duy toán học của học sinh.